Team Collaboration Particle Swarm Optimization and Its Application on Reliability Optimization
 , Xin Ma2, Xiaoqiang Zhang1, Huiying Gao1
, Xin Ma2, Xiaoqiang Zhang1, Huiying Gao1- DOI
- 10.2991/ijcis.d.210625.001How to use a DOI?
- Keywords
- Particle swarm optimization; Premature convergence; Optimization performance improvement; Reliability optimization
- Abstract
Particle swarm optimization (PSO) tends to be premature convergence due to easily trapping into local suboptimal areas. In order to overcome the PSO's defects, the reasons causing the defects are analyzed and summarized as population diversity deficiency, insufficient information sharing, unbalance of exploitation and exploration, and single update strategy. On this basis, inspired by human team collaboration behavior, a team collaboration particle swarm optimization (TCPSO) is proposed. Diversified updates strategies, dynamic grouping strategy, selectivity vector, and decreasing and increasing inertia weight are designed in TCPSO to solve the defects' reasons and improve the optimization performance. Eight typical test functions have been used to evaluate and compare the performance of different PSO variants, and the results have been proven that the optimal results found by TCPSO are better compared with other PSO variants, which demonstrates the rationality and effectiveness of TCPSO. Finally, a real-world problem for reliability optimization are solved by five algorithms, and the results prove the convergence rate and stable optimization performance of TCPSO, TCPSO can provide better support for reliability optimization of complex system.
- Copyright
- © 2021 The Authors. Published by Atlantis Press B.V.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
In recent years, the real-world optimization problems, such as nonlinear process control, mechanical structure design, system optimization, data clustering, flexible job-shop scheduling, resource provisioning and task scheduling, and so on, have become more and more complex, so that the traditional analytical algorithms are not able to satisfy the application demand. On the other hand, the swarm intelligence-based optimization algorithms, due to focusing on iteration calculation of optimized objects instead of describing the complicated mathematical expressions of optimization problems, can provide an effective solution to complex optimization problems [1,2]. Among lots of swarm intelligence-based optimization algorithms, particle swarm optimization (PSO) proposed by Kennedy and Ebenhart in 1995 has been one of the classic methods due to its concise mathematical description, few parameter setting and clear biological meaning [3].
PSO is inspired by the foraging behavior of birds, the population is made up of particles, and each particle can be described by position vector and velocity vector. The position vector represents the potential feasible solution of the problem, and the velocity vector represents the trajectory of the particle. In the process of searching for optimal solution, the individuals can be updated depending on their own experiences and population experience, so that the global optimal area can be found. Essentially, PSO is a heuristic swarm random search algorithm. However, lots of previous studies have proven that PSO tends to be premature convergence due to easily trapping into local suboptimal areas [4,5]. Undoubtedly, the applications of PSO are limited, especially for the complex optimization problems.
For overcoming the PSO defects, lots of modified PSO variants have been proposed. Basically, there are four modifying principles, and their brief overviews are listed as follows:
Parameters adjusting-based principle: Proper adjustment of control parameters such as inertia weight (IW), learning factor can accelerate convergence and in the same time avoid premature [4]. Because of its simplicity and operability, parameters adjustment has become an important modification to improve the PSO. A typical method of adjustment for inertial weight includes linear decreasing or increasing weight [6], self-weighted linear weight [7], Gauss distribution weight [8], fussy adaptive weight [9], and so on. Meanwhile, the adjustment based on learning factor can balance the individual cognition and population one, which mainly includes contraction factor (CF) and variable one [10,11]. Some papers also adopt adaptive adjustment based on IW and acceleration factor, which are proved to be effect for engineering optimization [12,13].
Neighborhood topology-based principle: In order to enhance the individuals' information communication and maintain the population diversity, lots of novel PSO variants based on researching on the particles in a neighborhood are proposed. Niche technique [14], dynamic neighborhood [15], neighborhood information sharing [16], and so on, they are widely used strategies for neighborhood topology. The advantage of this principle can balance the exploitation and exploration ability of PSO, which makes the optimization capacity of population better. The applications of neighborhood topology on PSO can be found in references [17,18].
Hybridized algorithm-based principle: The researchers have tried to integrate other evolutionary algorithms into PSO by the analysis and comparison, so that the advantages of other algorithms in search process can be utilized to overcome the defects of PSO. Selection, crossover and mutation operators in genetic algorithm (GA) have been introduced into PSO to enhance population diversity [19]. And a greedy search method has also been used to determine the Pareto parameter ε, so that the computational costs of PSO could be saved when handling the multi-objective optimization problems [20]. Moreover, differential evolution [21], simulated annealing [22], and immune algorithm [23] have also been effectively combined with PSO and achieved good results. Meanwhile, PSO variants combined with quantum behavior [24], chaotic behavior [25], and mutation regulation [26] have also been developed rapidly, which effectively improve the optimization performance.
Human behaviors-based principle: Nowadays, many PSO variants have been derived from the human behaviors; a new research approaches based on exploring and simulating of human behavior are opened. Human behaviors have good characteristics of diversity, interaction, dynamics, and adaptability. Traditional PSO can inherit many beneficial characteristics from human behavior, so that PSO variants have better performances in the engineering application. For example, these PSO variants may be based on human cognitive psychology [27], comprehensive learning strategy [28], human organization leadership behavior [29], aging mechanism of human society [30], human competitive and cooperative behavior [31], and so on.
Actually, these four modifying principles have only aimed at some reasons causing the premature convergence instead of all stated reasons, so the effect of improved optimization performance is limited and local. Therefore, in order to further improve the optimization performance, this paper would analyze and determine the main reasons causing the premature convergence. On this basis, inspired by human team collaboration behavior, comprehensive improved strategies basically aiming at all the reasons will be designed to overcome the defects of PSO. So the proposed PSO variant is named as team collaboration PSO (TCPSO).
Reliability is an important index to weight the comprehensive performances of various products in modern industrial society, reliability optimization can find an optimal design scheme under certain resource constraints, so that the system can obtain the highest reliability, or obtain the maximum economic benefit by minimizing the investments [32]. Therefore, more and more attentions have been paid to reliability optimization methods in today's manufacturing industry. Traditional methods, such as conjugate gradient method [33], constrained stochastic method [34], penalty function method [35], in addition, multidisciplinary design optimization method [36], GA [37] and simulated annealing algorithm (SAA) [38] are widely used in reliability optimization. In recent years, PSO has also been widely used in this field due to its simplicity and good optimization results. PSO based on multi-level penalty function was applied into the mechanical reliability optimization design, which improved the mechanical dynamic performance [39]. PSO based on Lévy flight was applied into the reliability optimization of hydraulic system [40]. A no speeds and coefficients PSO was proposed to optimize reliability problems [41]. An adaptive PSO was designed and applied into the reliability optimization of multi-objective system [42]. And a neighborhood fuzzy PSO was used to optimized a novel neural network for forecasting of software reliability [43]. In this study, TCPSO will be also applied into reliability optimization to verify its practical application effect.
The rest of the paper is organized as follows. In Section 2, the reasons causing PSO defects are analyzed detailedly. In Section 3, for overcoming the PSO defects, the novel TCPSO is proposed, and its performance is analyzed. Section 4 compares the performances of TCPSO and other PSO variants, and proves the merits of TCPSO. And in Section 5, TCPSO has been used to optimize the reliability and achieved better results. Finally, in the last section, conclusions are drawn.
2. THE ANALYSIS FOR REASONS CAUSING PSO DEFECTS
2.1. Traditional PSO Algorithm
The traditional PSO is always expressed as follows [1]:
2.2. The Stated Reasons Causing the Premature Convergence
As discussed above, PSO tends to be premature convergence due to easily trapping into local suboptimal areas. Essentially, there are four main reasons causing this situation, they can be summarized as (1) population diversity deficiency, (2) insufficient information sharing, (3) unbalance in the search process, and (4) single update strategy. Taking formula (1) as analyzed object, only two numbers r1 and r2 are generated randomly, which means the particles have hardly any opportunities to random mutation, obviously, the population diversity cannot be maintained. Formula (1) shows no mechanisms of information sharing among particles. Similarly, in the prophase and later of iteration, there are no any mechanisms for balancing exploitation and exploration. Actually, inertial weight ω can play the role of balancing. Moreover, besides depending on individual extremum pie, all the particles only follow the single extremum pge. Undoubtedly, the applications of traditional PSO are unsatisfactory, because it does not introduce the strategies that are conducive to overcoming premature convergence.
In fact, the four modifying principles were designed based on only solving part of reasons. Parameters adjusting-based principle mostly focuses on balancing the search process and individual update strategies; neighborhood topology-based principle mainly focuses on sharing population information and balancing the search process; hybridized algorithm-based principle focuses on population diversity, balancing the search process and individual update strategies; human behaviors-based principle basically focuses on population diversity and sharing population information.
3. THE TEAM COLLABORATION PSO
3.1. Team Collaboration Principle
Generally speaking, there are always elite and ordinary members in a team formed to achieve common goals. The elite members are in the minority and the ordinary members are in the majority. The contribution to team made by elite members is more effective than that of ordinary members; therefore, there is a collaborative relationship between elite and ordinary members, so that the elite members have to help ordinary members work better. Finally, they have to work together to get optimal result for their team. This description briefly summarizes team collaboration principle.
In the TCPSO, imitating the team collaboration behavior in human society, the population can be dynamically grouped into elite particles and ordinary particles based on their fitness values. At each iteration, the particles are sorted in a certain order, these ne particles ranked in the top are selected as elites, and the rest of no particles are ordinary. ne and no represent the number of elites and ordinary particles respectively. Actually this dynamic grouping strategy is similar to the neighborhood topology-based principle and maintains the channel of particle status change. Then these ordinary particles will be assigned an elite particle randomly, which means the ordinary particles can be updated under the influence of the different elite particles. This novel update strategy makes the majority follow multiple extremum rather than following only single extremum, which is beneficial to search more potential optimal areas. This multi-extremum following update strategy is explained as the first-type collaboration behavior. On the other hand, these ordinary particles who cannot improve the global extremum will be only guided by the elite particles to get better results. So this elite-guiding update strategy is defined as second-type collaboration behavior. Moreover, the elite particles will still be updated by following the single global extremum to explore the solution space. So that's why the proposed PSO is named as team collaboration PSO. Figure 1 shows the process of team collaboration.
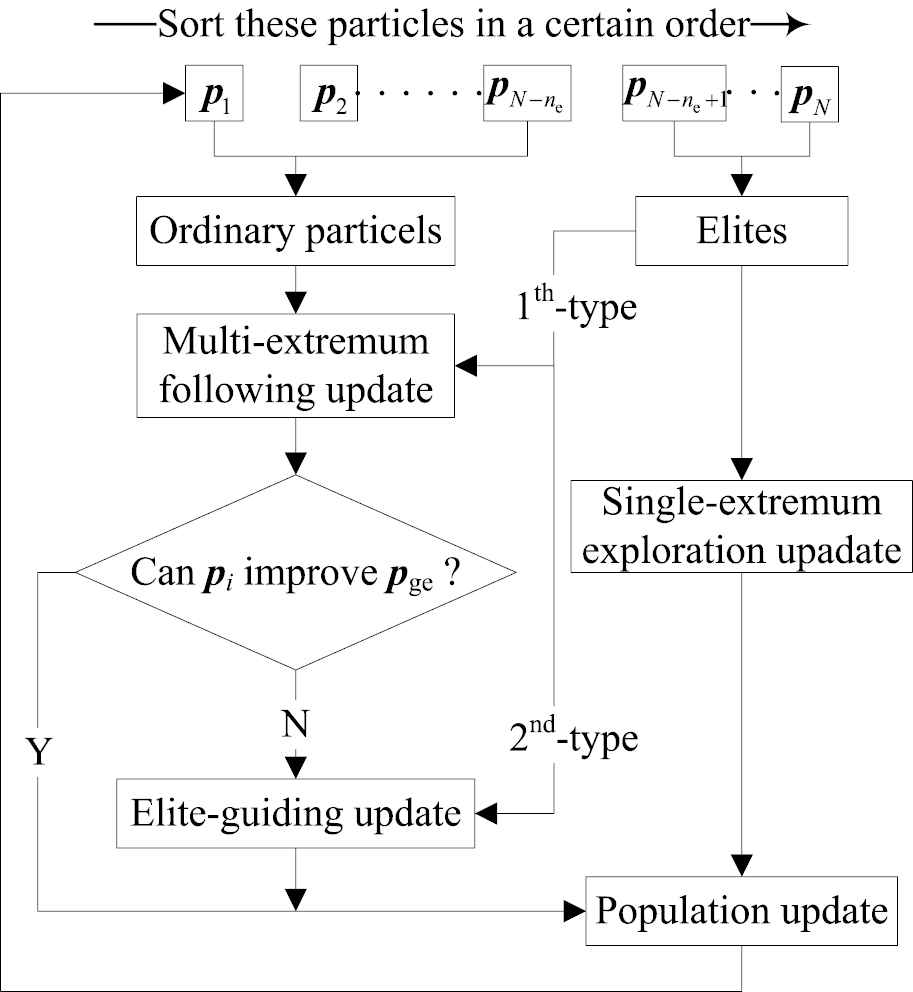
The principle of team collaboration PSO.
As shown in Figure 1, aiming at the reasons causing the PSO defects, more technical details will be discussed in the follow sections to show the advanced of TCPSO.
3.2. The Update Principle of TCPSO
3.2.1. Multi-extremum following update strategy
The mathematical description of the multi-extremum following update strategy is designed as follows:
Due to the poor optimization performances of ordinary particles, these ordinary particles have to follow the elite particles. Meanwhile, the elite particles are assigned to the ordinary particles randomly, which can increase the probability of searching more potential optimal areas and avoid trapping into local suboptimal areas. As for the ordinary particles, their own experiences are not authoritative. Essentially, it is not conducive to solving the optimal problem if completely depending on their po-ie. It is necessary to depend on the po-ie selectively, which can maintain the particles' diversity and convergence rate. So a1 is defined as selectivity vector, if the element
On the other hand, the collaboration mechanism is embodied in the third term of formula (2), elite particles can assist the ordinary particles to get better optimal results. Therefore, the multi-extremum following update strategy can be explained as the first-type collaboration behavior.
3.2.2. Elite-guiding update strategy
Multi-extremum following update strategy is a universal strategy in which all particles participate. After updating under the influence of elite particles, some particles can acquire better optimal results, while some particles cannot improve optimization performance. Accordingly, these relatively poor particles who can not improve the global extremum will be guided by elite particles to search more optimal areas. In elite-guiding update strategy, three guiding methods are proposed to cope with more complicated optimization problems, which includes overall guiding (OG), part guiding (PG), and random guiding (RG), they can be described as follows:
OG means that an ordinary particle is completely replaced by an elite particle, which can ensure that the individual extremum of ordinary particle can be improved. PG means that some elements of ordinary particles is replaced by continuous adjacent elements of elite, s1 and s2 denote the coordinates of the element in the particle vector, usually, 1 < s1 < s2 < D, D denotes the dimensionality of the particle. RG means that some elements of ordinary particles is replaced by the randomly selected elements of elite particle, α is also a D-dimension randomly generated binary vector.
According to elite-guiding update strategy, comparing the fitness values calculated by three methods, the guiding method that makes ordinary particle get best fitness value will be adopted to update ordinary particle. This strategy can increase the probability that the poor particles get better fitness values and improve the quality of population. In this strategy, the collaboration mechanism is embodied in the three guiding methods; moreover, compared to the first-type collaboration behavior, the collaboration between elite and ordinary particles is more direct and effective, which is a deep collaboration. So, the elite-guiding update strategy is defined as the second-type collaboration behavior. The mathematical expression of the elite-guiding update strategy is given in formula (8):
The elite-guiding update strategy is favorable for making the ordinary particles that cannot improve the global extremum converge to a relative optimal area, moreover, can avoid excessive congregation of ordinary particles and maintain the population diversity.
3.2.3. Single-extremum exploration update strategy
Unlike ordinary particles, the elite particles with relative better fitness values are responsible for finding the global optimal area, so that they mainly focus on exploring the solution space. They are updated by depending on their own experiences and following the global extremum, so the update strategy is single-extremum exploration update strategy, which is described as follows:
In this update strategy, ωe is an increasing IW, the initial value of ωe is also ωmax. The designed increasing inertia can make the elite particles explore more solution space for searching the global optimal area. Furthermore, ωo and ωe designed in TCPSO can balance the exploitation and exploration ability remarkably. Compared with the formula (2), there are two differences, the first is that elite particles only follow single global extremum, which means that the search processes of elite particles are always carried out based on improving the global extremum. Obviously, it helps to get the global optimal solution. The second is that the selectivity vectors are applied in the two terms of formula (9) rather than one term of formula (2). The selectivity vector a2 can enable the elite particles to reduce the over-dependency on the global extremum and avoid trapping into the local suboptimal areas at the late iteration due to following the single extremum.
3.3. Procedure of TCPSO and Its Performance Analysis
3.3.1. Procedure of TCPSO
The procedure of TCPSO is described as follows:
Step 1: Initialize each particle's initial velocity and position randomly. Essentially, the position of each particle can be regard as a potential solution. Random initialization can disperse the particles in the solution space with higher probability, thereby ensuring the population diversity.
Step 2: Calculate the particles' fitness values via the fitness function fit(·). And the particles are arranged in ascending or descending order according to their fitness values. These ne particles ranked in the top are selected as elites, and the rest of no particles are ordinary.
Step 3: The multi-extremum following update strategy is used to update the ordinary particles. If
Step 4: The elite-guiding strategy will help these ordinary particles who cannot improve the extremum. Ordinary particles need to randomly re-select elite particles. If
Step 5: The single-extremum exploration strategy is used to update the elite particles. If
Step 6: Repeat the above steps 2–5 until the terminal condition is met, then output the optimal solution. In this paper, the terminal condition is
3.3.2. TCPSO performance analysis
In order to obtain better global optimization performance, it is necessary to aim at the four reasons discussed above for improving PSO algorithm. TCPSO imitates the team collaboration in human society to acquire the advantage of adaptability, interaction, dynamic, and diversity in human behaviors, which improves the algorithm's performance greatly. Thus, Figure 2 shows the causality of performance improvement according to the technical method adopted by TCPSO.
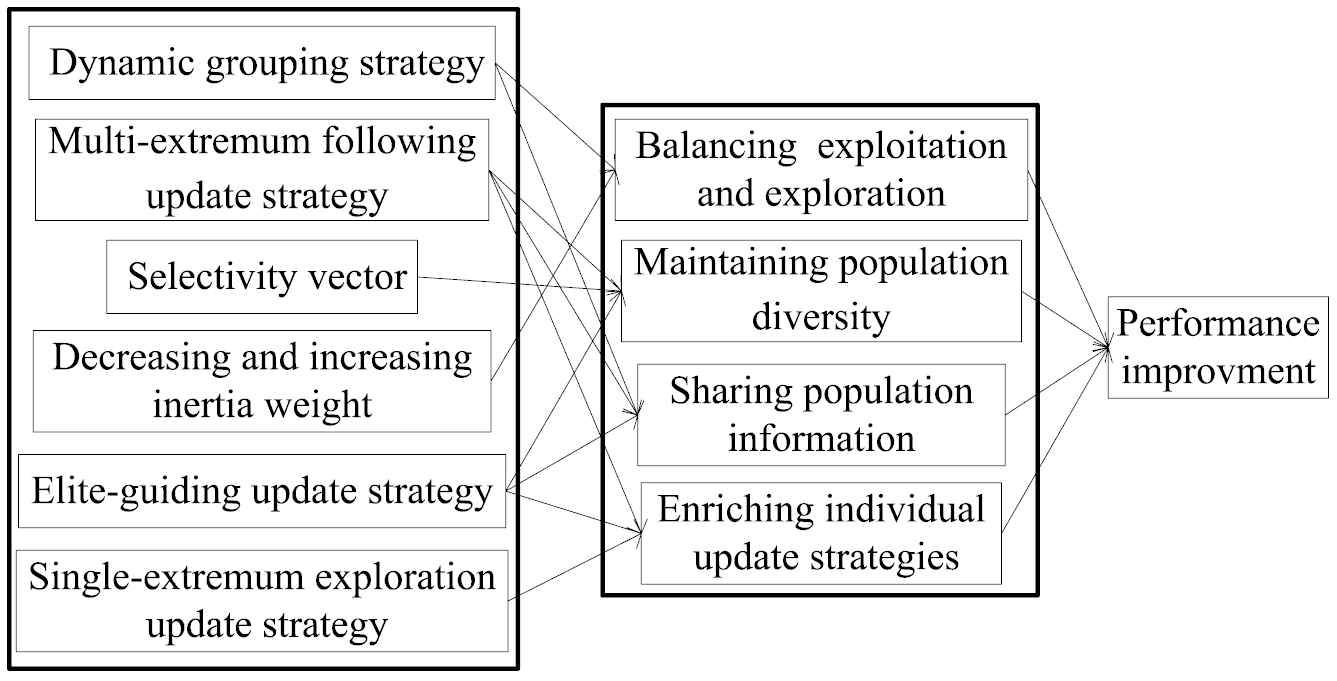
The causality diagram of performance improvement.
Particles are divided into elite and ordinary particles by dynamic grouping strategy. At the same time, the decreasing IW and increasing IW make the two kinds of particles always focus on exploration and exploitation respectively, so that the balance between exploration and exploitation can be kept in the iteration process.
Selectivity vector, multi-extremum following update strategy, and elite-guiding update strategy ensure that most of the particles have random mutation in the iteration process, thus maintaining the population diversity.
Dynamic grouping strategy always ensures that information from elite particles are shared. Moreover, multi-extremum following update strategy, and elite-guiding update strategy provide an open information exchange mechanism.
Five different individual update strategies give update richer and broader application, which not only change the particles' position, but also maintain the population diversity, and provide a channel of information sharing.
4. EXPERIMENTAL RESULTS AND PERFORMANCE VERIFICATION
PSO is a heuristic swarm random search algorithm. Like a double-edge sword, randomness is not only an inevitable guarantee for maintaining population diversity, but also an essential reason leading to difference in solving results [44]. Because of random initialization for the parameters such as positions and velocities, and the influence of different update strategies, even if the same optimization algorithm is used to solve a same problem, the final solution may be different. Some algorithms even lead to obvious difference of solutions, which are either in different local suboptimal areas or closer to the global optimal areas from different spatial directions. Accordingly, this phenomenon is explained as nonuniqueness of the solutions [45], which seriously affects the application of algorithms. Naturally, the fluctuation of fitness values is generated by the nonuniqueness of the solutions, so the performance of algorithms will be verified by the fluctuation range of fitness values.
Some typical test functions are used to test the performances of various PSO variants. Table 1 shows the relevant characteristics of eight test functions. The global optimal solutions of the eight functions are hidden in the 50-dimensional space with a width from −100 to 100 for each coordinate. Schaffer, Griewank, Ackley, and Rastrigin are typical nonlinear multimodal functions, which are generally recognized as complex optimization problems due to their innumerable local suboptimal solutions. For sphere, sum of different power function (SDPF), rotated hyper ellipsoid function (RHEF), and Rosenbrock, their global extremums are located in flat and narrow areas similar to parabolic canyons. Therefore, the information about the global extremums is difficult to obtain, so that many optimization algorithms can hardly cope with the four functions. Obviously, 8 test functions become a challenge for the PSO variants, which can verify their performances.
| Test Function | Search Range | Dimension | Optimal Solution | Global Extremum |
|---|---|---|---|---|
| Sphere: |
[−100, 100] | 50 | (0, 0, …, 0)50 | 0 |
| Schaffer: |
[−100, 100] | 50 | (0, 0, …, 0)50 | 0 |
| Griewank: |
[−100, 100] | 50 | (0, 0, …, 0)50 | 0 |
| Ackley: |
[−100, 100] | 50 | (0, 0, …, 0)50 | 0 |
| Rastrigin: |
[−100, 100] | 50 | (0, 0, …, 0)50 | 0 |
| Rosenbrock: |
[−100, 100] | 50 | (1, 1, …, 1)50 | 0 |
| SDPF: |
[−100, 100] | 50 | (0, 0, …, 0)50 | 0 |
| RHEF: |
[−100, 100] | 50 | (0, 0, …, 0)50 | 0 |
The characteristics of 8 typical test functions.
In the recent studies on PSO, the PSO variants based on human behaviors-based principle have received more attentions. For example, self-regulating PSO (SRPSO) imitating human cognitive psychology [27], aging leader and challengers PSO (ALCPSO) imitating aging mechanism of human society [30], adaptive PSO with supervised learning and control (APSO-SLC) [46], and composite PSO with historical memory (HMPSO) [47] have been proven to be excellent optimizer. Meanwhile, some PSO variants based on parameters adjusting-based principle, including IW and CF strategy [48,49], have been applied to solve many practical engineering problems. In addition, the PSO variant based on dynamic neighborhood topology (DNPSO) [50] and enhancing comprehensive learning PSO with local optima topology (CLPSO-LOT) [51] are widely used for optimization problems. The PSO variants combined with simulated annealing (SAPSO) [22], multiple agents (MAPSO) [52] and differential evolution PSO (DEPSO) [53] have improved the performance of traditional PSO. Therefore, SRPSO, ALCPSO, APSO-SLC, HMPSO, IWPSO, CFPSO, DNPSO, CLPSO-LOT, SAPSO, MAPSO, and DEPSO will be compared with TCPSO to verify the performance of the proposed algorithm.
4.1. Performance Comparison and Analysis for PSO Variants
In this study, the statistical parameters including mean and standard deviation (STD) of global extremums obtained by 100 repeated experiments are used to verify the performances. For these PSO variants, the population size is 60, the
| Algorithm | Statistics | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 |
|---|---|---|---|---|---|---|---|---|---|
| SRPSO | Mean | 2.5242e−04 | 0.4481 | 0.0055 | 21.1626 | 193.3532 | 155.0830 | 3.1507e+08 | 917.4161 |
| StD | 4.2361e−04 | 0.0159 | 0.0066 | 0.0591 | 47.8580 | 99.5176 | 2.2950e+09 | 325.5636 | |
| ALCPSO | Mean | 8.4617 | 0.4548 | 0.3550 | 19.2621 | 950.8462 | 5.2190e+03 | 1.2248e+24 | 1.0312e+03 |
| StD | 3.5402 | 0.0143 | 0.1003 | 1.7590 | 247.1140 | 5.2917e+03 | 6.2171e+24 | 400.3505 | |
| APSO-SLC | Mean | 1.2505e−16 | 0.0097 | 1.11027e−17 | 4.8554e−15 | 9.0949e−14 | 47.4249 | 5.0692e−22 | 6.6905e−16 |
| StD | 9.1053e−17 | 2.0771e−17 | 3.3645e−17 | 1.7431e−15 | 6.9378e−14 | 0.5795 | 1.3372e−21 | 2.6897e−16 | |
| HMPSO | Mean | 0.0048 | 0.4607 | 4.2305e−04 | 19.0032 | 300.4377 | 58.2764 | 3.8004e−06 | 46.8874 |
| StD | 0.0039 | 0.0051 | 8.5321e−04 | 0.0152 | 93.4389 | 9.7114 | 2.2231e−05 | 13.4435 | |
| IWPSO | Mean | 474.2775 | 0.4451 | 1.1099 | 19.7884 | 1.1198e+03 | 5.8911e+05 | 1.4861e+38 | 1.0436e+04 |
| StD | 170.3416 | 0.0176 | 0.0337 | 1.2198 | 253.8437 | 4.2853e+05 | 1.3597e+39 | 4.5818e+03 | |
| SFPSO | Mean | 1.9491e+03 | 0.4886 | 1.4751 | 20.6655 | 2.6131e+03 | 2.0591e+07 | 1.4339e+49 | 6.8552e+03 |
| StD | 487.0422 | 0.0048 | 0.1139 | 0.3983 | 493.3263 | 8.9704e+06 | 1.4305e+50 | 1.9304e+03 | |
| DNPSO | Mean | 0.1176 | 0.4995 | 0.0105 | 20.0057 | 471.2133 | 180.5542 | 0.0019 | 675.4832 |
| StD | 0.2309 | 4.4917e−04 | 0.0154 | 0.0103 | 123.0914 | 65.6856 | 0.0073 | 1.7240e+03 | |
| CLPSO-LOT | Mean | 0.0047 | 0.4433 | 0.0071 | 5.0971 | 223.9392 | 100.6991 | 60.9934 | 552.2142 |
| StD | 0.0021 | 0.01845 | 0.0076 | 3.1727 | 52.4174 | 99.7014 | 23.4539 | 102.3495 | |
| SAPSO | Mean | 132.2141 | 0.4455 | 0.9869 | 19.4486 | 1.1760e+03 | 2.6430e+05 | 9.6887e+35 | 2.5067e+03 |
| StD | 53.1313 | 0.0182 | 0.0593 | 1.7836 | 212.5357 | 1.8261e+05 | 7.9557e+36 | 1.2099e+03 | |
| MAPSO | Mean | 0.0047 | 0.4127 | 0.0049 | 18.6537 | 206.6578 | 150.3267 | 7.4364e+07 | 553.5643 |
| StD | 0.0062 | 0.0423 | 0.0061 | 4.5478 | 43.1278 | 76.1372 | 3.4321e+07 | 214.6424 | |
| DEPSO | Mean | 0.2837 | 0.1799 | 0.0597 | 2.8268 | 270.3788 | 1.2161e+03 | 4.4037e+08 | 1.6623e+03 |
| StD | 0.1165 | 0.0432 | 0.0299 | 0.8465 | 56.4141 | 1.3556e+03 | 1.6553e+09 | 738.4271 | |
| TCPSO | Mean | 5.4995e−93 | 0 | 0 | 0 | 0 | 42.5388 | 1.0680e−227 | 8.5716e−148 |
| StD | 4.7304e−92 | 0 | 0 | 0 | 0 | 0.8171 | 0 | 8.5697e−147 |
Bold values highlight the advantage of TCPSO's performance, which is conducive to results' comparison.
Statistical results' comparison of PSO variants.
Table 2 shows that for all the complex test functions, TCPSO can find better solutions than the solutions found by other PSO variants. Basically, excepting in the Rosenbrock function, TCPSO has found the global optimal solutions, while other PSO variants can hardly obtain global optimal solutions when solving such complex multimodal optimization problems due to simplicity of improved principles. These PSO variants are only useful for some test functions rather than all functions. Moreover, TCPSO is proved to have better stability and reliability, the influence of randomness on PSO is suppressed, the nonuniqueness of solution is effectively overcame. The comparison results demonstrate the feasibility of the improved idea proposed in this paper, which can provide a theoretical support for expanding the application of PSO.
As previously discussed, on the basis of studying the inherent defects of PSO, the strategies designed in TCPSO can deal with four reasons causing premature convergence. In order to compare the convergence performance, the global extremum curves drawn by the computations that finding the best optimal solution in 100 repeated iterations are used to compare the PSO variants' performances. The comparison results are shown in Figure 3. These figures intuitively show the TCPSO can quickly converge to a relatively optimal solution area and find the optimal solutions whit higher quality, so that TCPSO is more advantageous for engineering practice application.
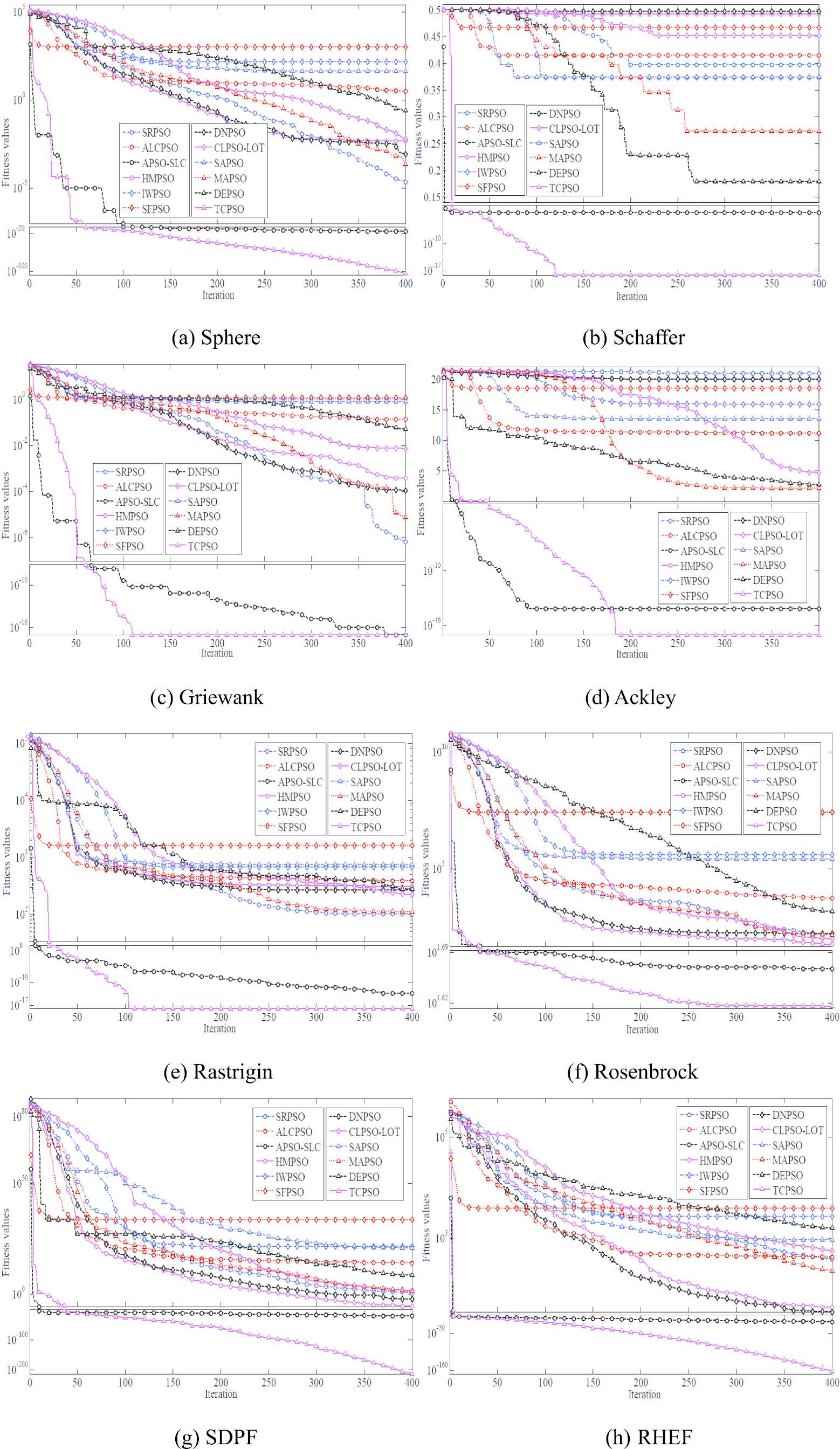
Comparison of global extremum curves for different functions.
4.2. Influence of Parameters on TCPSO and Its Analysis
Like many other algorithms, some parameters need to be adjusted manually, which has a significant impact on the performances of the algorithms [54]. TCPSO also has adjustable parameters, among which the main uncertain parameter is the number of elite particles ne. In previous verifications, ne is set as 3. Therefore, in order to verify the influence of different ne, ne is set as 1 to 15 for performance verification. The other settings of TCPSO are as same as Section 4.1. Similarly, 100 repeated experiments are done for verifying the performance. Figure 4 shows the influence of different ne.
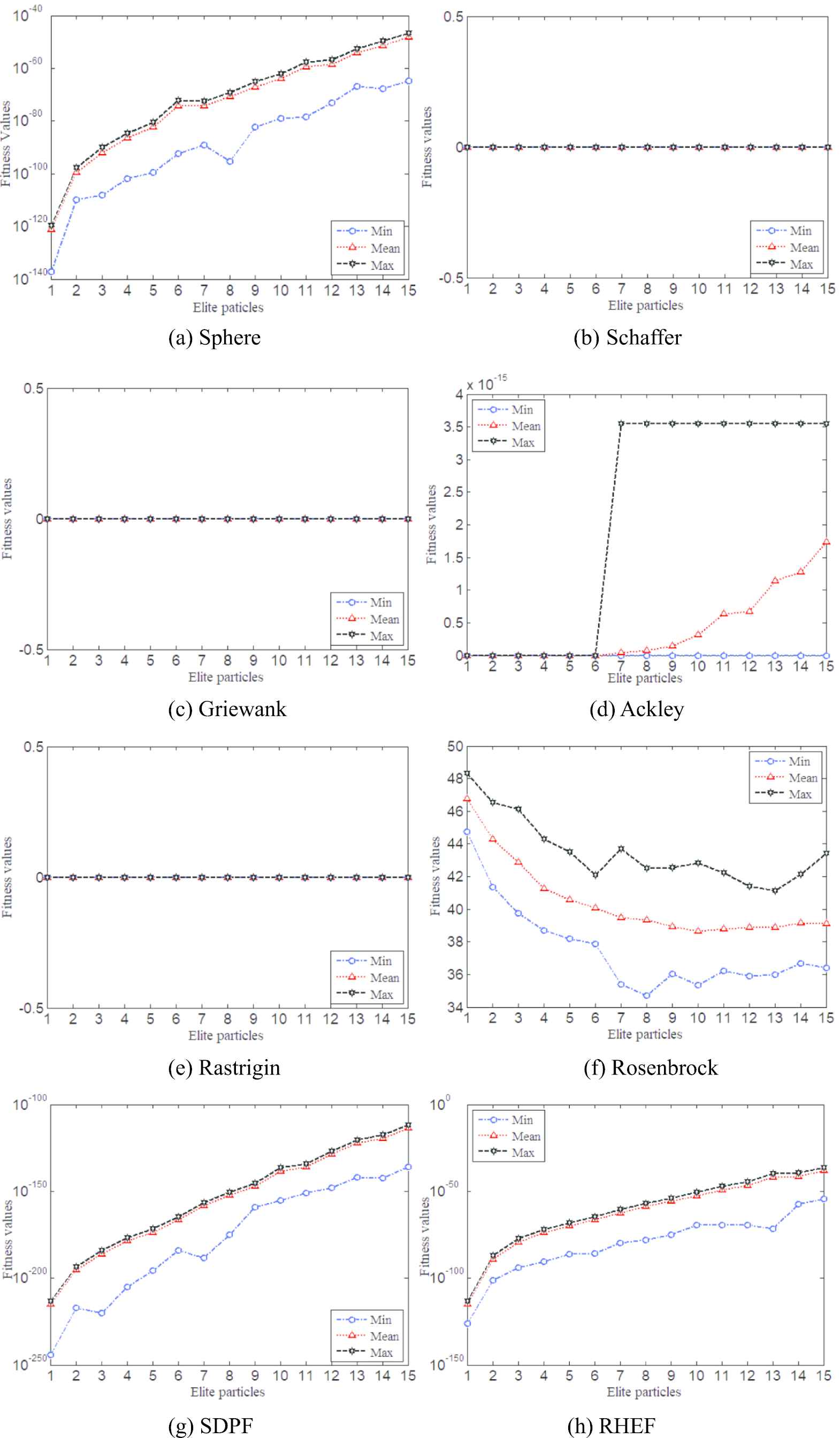
Influence of ne change on TCPSO performance for different functions.
As shown in Figure 4, for Sphere, Ackley, SDPF, RHEF, when
4.3. Verification for the Effect of Update Strategies
The update strategies designed in TCPSO include multi-extremum following update strategy, elite-guiding update strategy, and single-extremum exploration update strategy. The elite-guiding update strategy includes OG, PG, and RG. Actually, the update strategies that can update global extremum are only multi-extremum following update strategy, single-extremum exploration update strategy, PG, and RG. The function of OG just improves the individual extremum of ordinary particle rather than global extremum. In order to verify the update effect of these four update strategies, how many times the global extremum changed by the four update strategies will be counted, the percentages among the updates caused by the four strategies respectively and the total updates are used to evaluate the contributions of different update strategies, so that the rationality of the proposed TCPSO can be further verified. The settings of TCPSO are completely similar with Section 4.2. Figure 5 shows the percentage of update number caused by each strategy in the process of optimization.
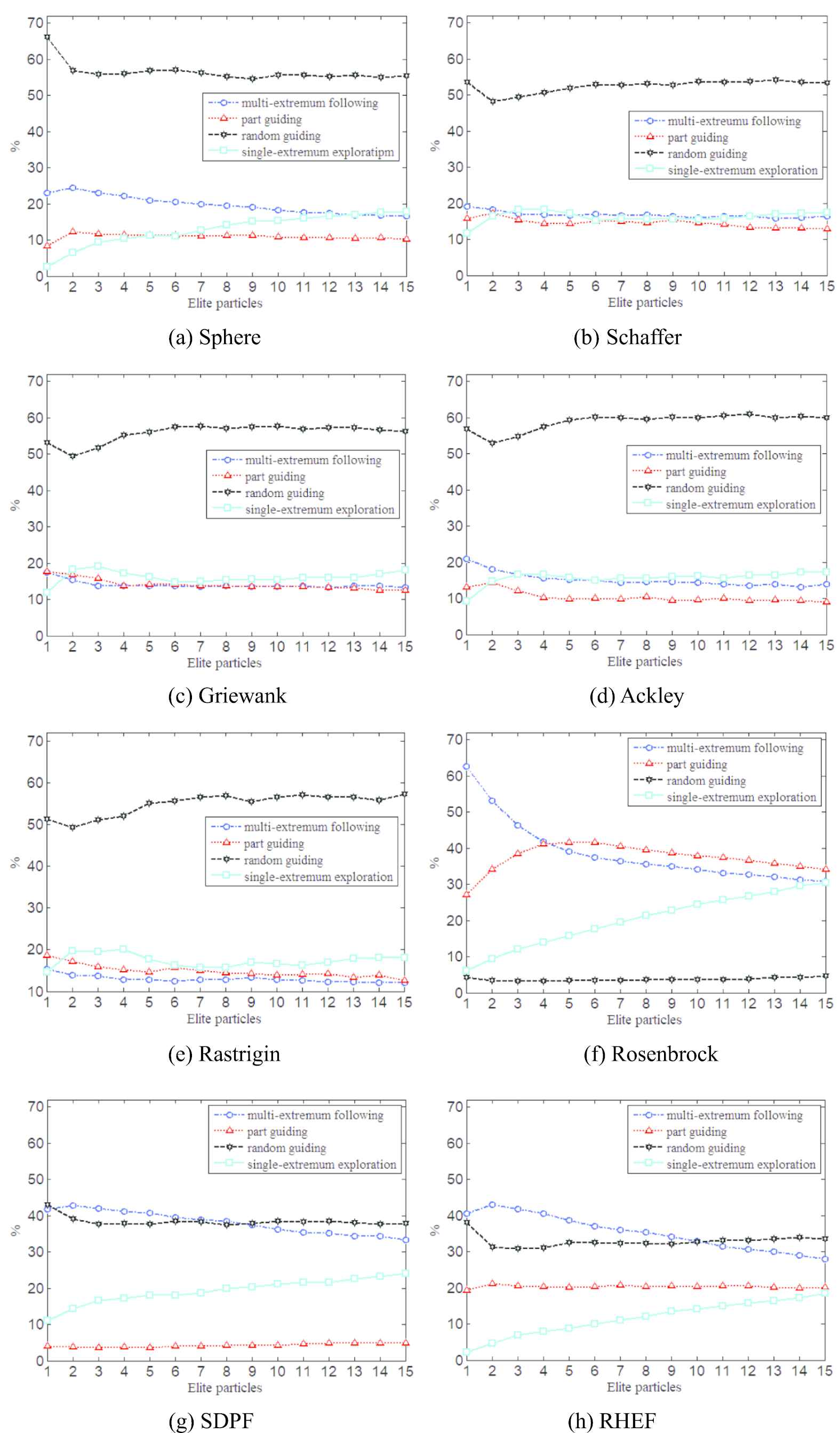
Contributions of different update strategies to the functions optimization.
As shown in Figure 5, for sphere, Schaffer, Griewank, Ackley, Rastrigin, RG plays a major role in updating global extremum. For SDPF and RHEF, multi-extremum following plays a basically equal role with RG in updating global extremum. For Rosenbrock, multi-extremum following plays a basically equal role with PG in updating global extremum. Therefore, each update strategy can play an important role in improving the global extremum according to the different characteristics of objective functions. The TCPSO is proved to ensure the global extremum is found with a higher probability when solving high-dimensional, complex, multi-parameter optimization problems.
5. TCPSO PERFORMANCE ON THE RELIABILITY OPTIMIZATION
Reliability redundancy allocation is the widely accepted reliability optimization technique, which is helpful to balance the safety and cost of the complex system. In this section, the performance of TCPSO is studied for the reliability redundancy allocation of complex system, we have 3 assumptions for this problem: (1) the failures of units in the system are independent; (2) the reliability and cost of each redundant unit in the subsystem are known; (3) each unit has only two states: normal and failure.
A reliability redundancy allocation problem of a typical complex system is used to verify the algorithm performance. The reliability block diagram of the typical complex bridge system is shown in Figure 6.
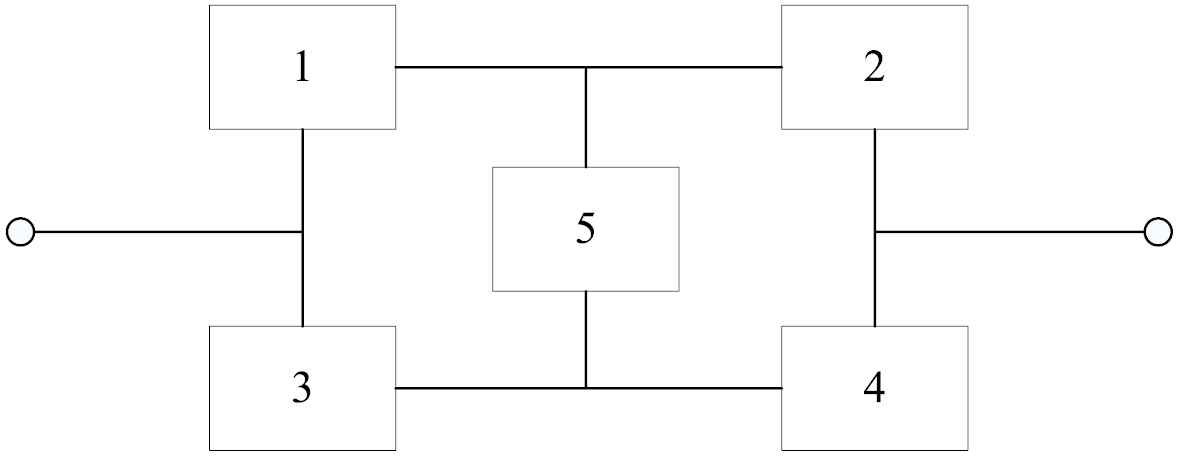
Reliability block diagram of complex bridge system.
In each subsystem, the redundancy is formed by parallel connection of units, so the reliability of each subsystem can be calculated by formula (12):
Therefore, let ci denotes the cost of unit in the ith subsystem, let Cs denotes the total cost of the system. The reliability redundancy allocation model is written as follows:
The reliabilities and costs of the units in different subsystems are given in Table 3. The concept of cost in Table 3 is only a numerical reflection for value, therefore, it has no corresponding unit.
| Subsystem | 1 | 2 | 3 | 4 | 5 |
| Unit reliability | 0.70 | 0.85 | 0.75 | 0.80 | 0.90 |
| Cost | 2 | 3 | 2 | 3 | 1 |
The reliabilities and prices of the units in different subsystems.
Because PSO is difficult for outputting a integer solution, so we let P = [round(x1), round(x2), round(x3), round(x4), round(x5)], xi is a real number, round(·) is a rounding function, ni = round(xi). For constrained optimization problems, the fitness function of TCPSO can designed as follows:
Obviously, reliability redundancy allocation is a minimum optimization problem, the cost or the reliability of system are decreased or increased respectively, which can achieve an optimal solution.
For comparing the performances of different algorithms, quantum particle swarm optimization (QPSO) [56], ant colony optimization (ACO) [57], GA [58], and SAA [59] are used to optimize the reliability redundancy of the bridge system. For the 4 algorithms, the population size is 40, the
| Algorithms | Optimal Solution | Cs | Rs | Proportion of Optimal Solution | Average Step of Optimal Solution |
|---|---|---|---|---|---|
| TCPSO | [1, 1, 3, 1, 2] | 16 | 0.9945 | 100% | 4.3 |
| QPSO | [1, 1, 3, 1, 2] | 16 | 0.9945 | 84% | 60.8 |
| ACO | [2, 1, 2, 1, 2] | 16 | 0.9939 | 76% | 43.8 |
| GA | [2, 1, 2, 1, 2] | 16 | 0.9939 | 78% | 55.7 |
| SAA | [2, 1, 3, 1, 1] | 17 | 0.9939 | 67% | 83.6 |
The performance of 4 algorithms in reliability redundancy allocation.
6. CONCLUSIONS
In this paper, the reasons causing the premature convergence are analyzed, and TCPSO imitating human team collaboration behavior is proposed to overcome the inherent defects of PSO, TCPSO can maintain the population diversity, share population information, balance exploitation and exploration, enrich individual update strategies well, so that TCPSO possesses better global optimization performance when solving the complex multimodal optimization problems. Different typical characteristic test functions are used to evaluate TCLPSO, and the comparisons with some latest PSO variants are conducted. The optimization results demonstrate that TCPSO consistently performs better than other PSO variants and has stable and reliable global optimal ability. The good performances expand the application space of PSO, and provide a technical support for real-world engineering problems, such as reliability optimization of complex system.
CONFLICTS OF INTEREST
The authors declare no conflict of interest.
AUTHORS' CONTRIBUTIONS
Bo Zheng performed algorithm designing and analysis, verified algorithms, and wrote the manuscript. Xin Ma performed algorithm programming. Xiaoqiang Zhang and Huiying Gao helped perform the analysis with constructive discussions.
ACKNOWLEDGMENTS
This study was supported by the Project of Sichuan Province Science and Technology program (No. 2021YJ0519); China Civil Aviation Administration Development Foundation Educational Talents Program (No. 14002600100018J034); General Foundation of Civil Aviation Flight University of China (No. Q2019-053); Youth Foundation of Civil Aviation Flight University of China (No. Q2018-139).
REFERENCES
Cite this article
TY - JOUR AU - Bo Zheng AU - Xin Ma AU - Xiaoqiang Zhang AU - Huiying Gao PY - 2021 DA - 2021/07/01 TI - Team Collaboration Particle Swarm Optimization and Its Application on Reliability Optimization JO - International Journal of Computational Intelligence Systems SP - 1842 EP - 1855 VL - 14 IS - 1 SN - 1875-6883 UR - https://doi.org/10.2991/ijcis.d.210625.001 DO - 10.2991/ijcis.d.210625.001 ID - Zheng2021 ER -
