Polar Code Appropriateness for Ultra-Reliable and Low-Latency Use Cases of 5G Systems
- DOI
- 10.2991/ijndc.k.190702.005How to use a DOI?
- Keywords
- Polar code; URLLC; 5G New Radio; reliability; decoding latency; LDPC code
- Abstract
Polar code is considered as a major breakthrough of past decade in channel coding area. The unprecedented performance of polar codes compelled third generation partnership project (3GPP) to adopt the polar codes for control channels functions in one of the fifth generation (5G) scenario enhanced mobile broadband (eMBB). No decision has been made yet on channel coding for remaining 5G scenarios namely, Ultra-Reliable and Low-Latency Communication (URLLC) and Massive Machine Type Communication (mMTC). This paper focuses on channel coding schemes particularly for URLLC use case of 5G New Radio (5G-NR) and evaluating the performance of polar codes for the same. Polar codes are investigated on the basis of various performance parameters for short block lengths and low code rates as desired for URLLC scenario. The excellent error correcting performance of highly reliable polar code with low computational complexity and low decoding latency makes it a strong contender in URLLC channel coding race.
- Copyright
- © 2019 The Authors. Published by Atlantis Press SARL.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
Fifth generation (5G) and the future wireless networks will going to endorse innumerous emerging use cases and applications with various performance aspects. Concerning this, ITU-R in September 2015 agreed upon its vision for IMT-2020 and beyond networks [1], and outlined three main 5G usage scenarios: (i) Enhanced Mobile Broadband (eMBB); (ii) Ultra-Reliable and Low-Latency Communication (URLLC); and (iii) Massive Machine Type Communication (mMTC). Therefore, new technologies for 5G has been driven by these specific uses to provide ubiquitous connectivity to all the diverse applications. 5G New Radio (5G-NR) is not just an addendum advancement over 4G Radio Access Technologies (4G-RAT), instead 5G technology is very different. The NRAT for 5G (5G-NRAT) includes combinational influence of various new technologies like, new heterogeneous cellular architecture, all new GHz frequency bands with huge available bandwidths, massive MIMO, millimeter wave communication, mMTC, Internet-of-Things (IoT) etc.
Moreover, the selection of efficient channel coding method is also very potent game changer in any mobile generation. Channel coding for 5G-NR is facing novel challenges as to uphold and encourage various emerging use cases and new applications. Therefore a paradigm shift in channel coding techniques is suggested for 5G scenarios [2]. However, the state-of-the-art channel codes, i.e. turbo and Low density parity check (LDPC) codes which are key enablers in existing third and fourth generation (3G) and (4G) mobile systems [UMTS and Long Term Evolution (LTE)] are already unproven for many new 5G applications [3]. Industry and academia are working to find an efficient and powerful method of channel coding that fulfil the requirements of all diverse 5G applications. In search of efficient coding method for future generations, the polar code emerges as a prominent advancement in the channel coding area in past decade.
Polar code, invented by Arikan [4] is considered as a strong contender in race of 5G channel coding techniques. In 3G partnership project (3GPP) Release-15, a decision was made on channel coding for 5G-eMBB scenario where polar codes replaced the tail biting convolutional code (used as channel code for control channel functions in 4G) [5]. 3GPP decided in RAN 86 and 87 meetings to standardize LDPC codes for data channels and polar codes for control channel in 5G-eMBB scenario. Polar code also find their application over the physical broadcast channel. No decision has been made yet on channel coding for remaining use cases, i.e. URLLC and mMTC. This is an open issue for research and 3GPP has already started its contribution from RAN 85. This paper focuses on evaluation of channel coding methods particularly for URLLC use case.
Channel coding design issues for URLLC scenario is defined in next section which are very complicated to comprehend due to two adverse demands of this scenario: (i) Ultra-high reliability and (ii) low latency [6]. Polar code can achieve the excellent error performance with reliability of 99.999% and very low latency of order of 1 ms. Moreover, higher coding gain with no error floor and low complexity decoding methods make polar code more attractive for URLLC use case. Apart from this, data rate demands for URLLC are comparable to that of the control channels and polar code has been already won the race of control channel coding in eMBB scenario [7]. Therefore, polar code can be anticipated as a most powerful contender for URLLC scenario among all FEC candidate codes.
This paper focuses on channel coding schemes particularly for URLLC use case and analyses all FEC candidates under consideration. Polar codes are investigated for their Error correcting [Block Error Rate (BLER)] performance, reliability and error floor performances, computational complexity and decoding latency. Performance of polar code in terms of BLER versus Es/N0 is evaluated and compared with that of LDPC code for short information block lengths and low code rates as desired for URLLC use case.
This paper is organized as follows: In Section 2, channel coding requirements for URLLC scenario are highlighted; FEC candidates for URLLC are presented in Section 3. In Section 4, performance evaluation of polar codes for URLLC scenarios through simulation results is discussed and compared with LDPC codes for various information block lengths and code rates.
2. CHANNEL CODING REQUISITES FOR 5G-URLLC SCENARIO
This section briefly explains major requirements of NR-URLLC use case and maps those requirements on channel coding methods. URLLC use case of 5G-NR imposes strict requirements on two conflicting parameters: (i) low latency and (ii) ultra-high reliability [8]. Lowering the latency requires short information that results in lower coding gain and reliability deterioration. On the other hand, increasing the reliability requires more parity/redundancy bits added to the information and sometime retransmission which will result in higher latency. Therefore, selection of the channel coding method for this scenario should be done wisely. After adopting standards for eMBB scenario, 3GPP started working toward 5G-URLLC scenario [9]. 3GPP in endorsement with IMT-2020 defines the key performance indicator requirements of 5G-URLLC [7]:
- (i)
Latency: The overall end-to-end latency is 1 ms (0.5 ms for uplink transmission and 0.5 ms for downlink) for one packet.
- (ii)
Reliability: The transmission reliability is defined in terms of targeted BLER of 10−5 within 1 ms period with or without support of Hybrid automatic repeat request (HARQ). Moreover, the error floor free BLER performance with higher coding gain is desired for the ultra-high reliability of order of 99.999% and beyond.
These URLLC demands of short latency and high-reliable transmission are calibrated for the channel coding techniques. Although NR-URLLC specifications are still under study, some of its major suggestions for characteristics of the optimum channel coding scheme would be defined by Figure 1 [7,8,10,11].
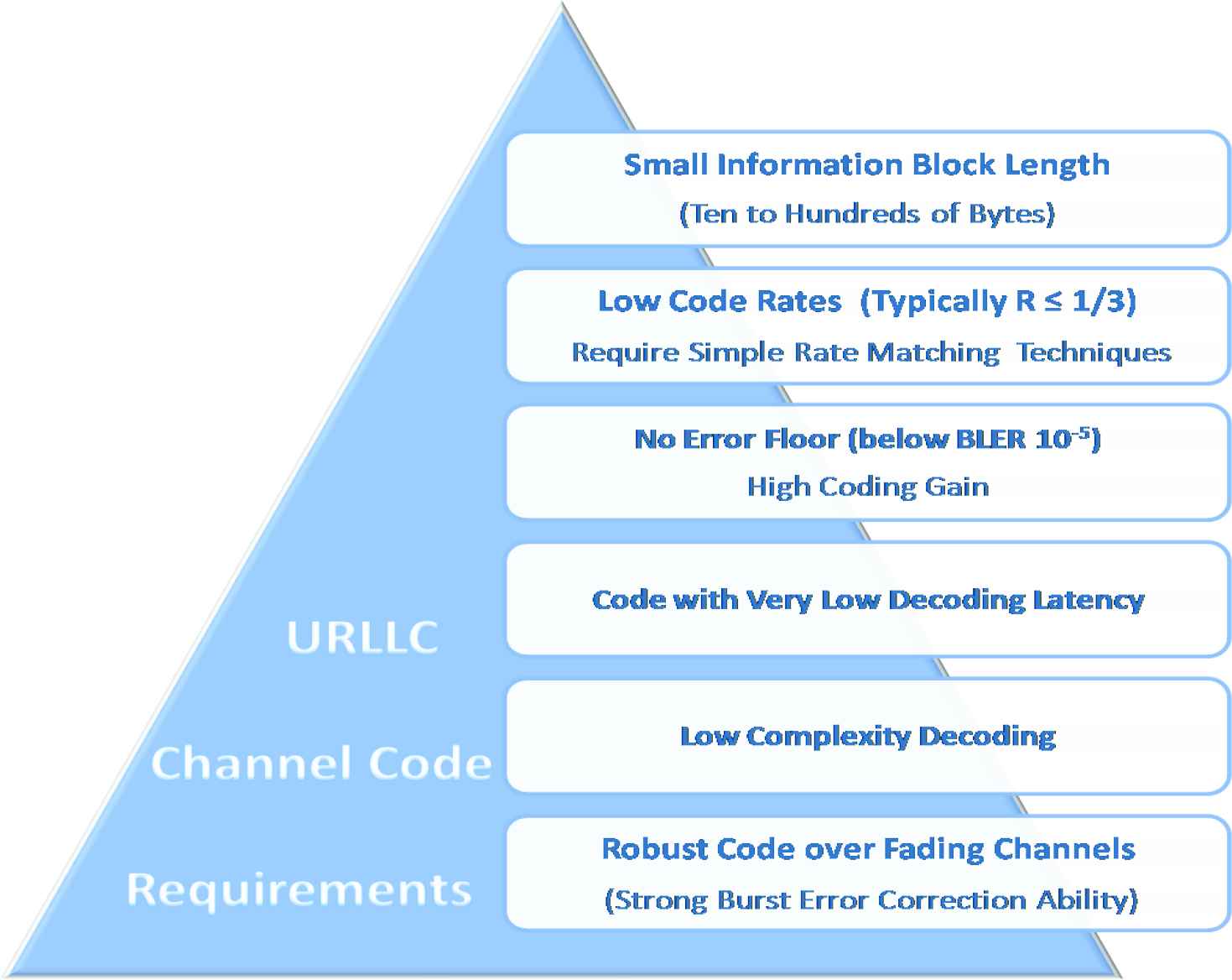
Requirements for channel coding in NR-URLLC scenario. NR, new radio; URLLC, ultra-reliable and low-latency communication.
A paradigm shift in state-of-the art coding techniques is mandatory to find an efficient channel coding methods for such high reliability and low-latency requisites of NR-URLLC. The optimum channel coding scheme verdict is an open issue to be discussed for 5G-URLLC scenario.
3. CHANNEL CODE NOMINEES FOR 5G-URLLC
After Shannon’s coding theory, various channel coding schemes are proposed, from capacity approaching to capacity achieving that perform good over larger block lengths. But some powerful codes like convolutional, turbo, LDPC and polar codes exhibit promising performance for shorter block lengths and lower code rates, therefore, are examined for URLLC scenarios.
3.1. Turbo Code
Turbo code invented in 1993 [12], uses parallel concatenation of two convolutional codes at the encoder and serial concatenation at the decoder. The concept of interleaver raises the error performance very near to the Shannon’s limit. Turbo codes are used in deep space communication, digital video broadcasting and are also key enablers in 3G and 4G (both UMTS and LTE services). Unfortunately, turbo codes are already out of 5G race. This is because of (i) poor BLER performance for shorter block lengths and at low code rates, (ii) high complexity iterative decoding results in low throughput and high latency, (iii) presence of error floor makes them unfit for high reliability applications [11]. This is why, turbo code is considered to be inadequate for 5G-URLLC scenario.
3.2. LDPC Code
LDPC code rediscovered in 1997 [13], is a linear block code that has sparse parity check matrix, H, with low density of 1’s. LDPC codes have outstanding capacity approaching performance, even better than turbo codes in terms of error floor, decoding complexity and for high code rate. LDPC codes find their applications in WiMAX 802.16 and various IEEE standards. LDPC codes are admired for their fabulous performance for larger block lengths and high code rate. For this reason, 3GPP standardized LDPC codes for data channels in 5G-eMBB scenario [14].
But, LDPC code is not a good choice for 5G-URLLC use case because, (i) all of the proposed LDPC decoders (normalized offset min sum, normalized layered min sum, etc.) show inferior performance for short block lengths (<400 bits) and low code rates (R < 1/3) [15,16], (ii) Practical implementation complexity and iterative decoding complexity is high in case of small blocks and low code rate. Otherwise, LDPC codes decoders are least complex for larger blocks and higher rates. (iii) Error floor occurs with LDPC code when small blocks are considered. (iv) Short decoding latency is not true for very low code rates [11]. Low code rate and short block length needs more number of iterations that will lead to higher computational complexity [17], higher power consumption and hence, longer decoding latency for equivalent performance.
3.3. Tail Biting Convolutional Code
Long Term Evolution-Tail Biting Convolutional Code (LTE-TBCC) finds its application in LTE systems as a channel coding scheme for control channels. These codes show good performance for short block lengths but same is not true in case of low code rates [18]. Also, due to tail biting, extra operations are needed before the decoding begins. This will enhance the decoder complexity, and hence, increase the decoding latency [11,19,20].
3.4. Polar Code
Arikan [4] introduced the polar codes as a class of linear block codes that were first explicitly proven capacity achieving channel codes. Polar codes break the wheel in channel coding area with its unconventional perspective of code construction than that of the traditional codes and become a youngest contender in the 5G race. Additionally, simple encoder with modest complexity SC decoder renders polar code attractive for a lot of 5G applications.
Polar codes are established by the concept of channel polarization where, N copies of an ordinary channel W [with capacity I (W)] are transformed into extreme channels whose symmetric capacities reach either 1 or 0, as N goes large. These obtained N polarized channels are either (i) perfect/reliable channels which transmit noiselessly (with max. capacity of 1) or (ii) extremely noisy/unreliable channels that transmit only random noise. Then, the polar encoder transmits K information bits over reliable channels while remaining N–K bits are made frozen bits (0 or 1) and transmitted over unreliable channels.
The fundamental polar decoder is Successive Cancellation (SC) decoder that can provably achieve the Shannon’s capacity with modest complexity. Various improved SC decoding algorithms have been proposed for betterment of the finite length performance of polar code in Tal and Vardy [21] and Ercan et al. [22]. SC-List (SCL) decoders are currently investigated for 5G studies that use L simultaneous decoding paths to get improved performance over MAP decoders. Cyclic redundancy check (CRC) aided polar code (CA-Polar) with SCL decoding can even surpass state-of-the art codes (LTE-turbo code and LDPC code). Parity check polar code (PC–CA Polar Code) has been recommended for low-latency applications, hence, considered for URLLC scenario [23].
Parity check–CRC aided polar codes in Figure 2 uses distributed CRC and PC bits to attain maximum benefits from assistant bits. CRC bits are distributed over a block and used for error detection and potentially for early termination. However, PC bits are distributed in reliable and unreliable locations and assist in error correction and early termination. Both CRC and PC bits in conjunction with SCL decoder help in improving the polar code performance. But, PC bits improve distance spectrum and provide additional coding gain due to its early intervention.

Systematic block diagram of PC–CA polar code. PC, parity check; CA, CRC aided.
4. COMPATIBILITY OF POLAR CODE FOR 5G-URLLC
All channel coding candidates of URLLC scenario are discussed in last section. This section provides some highly probable aspects for the appropriateness of polar codes for URLLC use case. A Chinese firm Huawei is the main leader that brings polar codes as a channel coding method in 5G field trials and in October 2016, and it achieved the downlink speed of 27 Gbps [24]. Also, in 3GPP meetings, polar code replaced deep rooted turbo codes in 5G-eMBB scenario and over physical broadcast channels.
Lot of research is going on the channel coding methods for URLLC case and the winner has not been announced yet. Polar codes are considered as the most acceptable contender in this contest. This is because; supreme error correcting performance for short information block lengths at low code rates with easy code shorting and puncturing mechanisms respectively [11,19,20]. For this, polar codes have lower SNR requirements when compared with other candidate codes for similar error rate, hence, attain higher coding gain and enhanced spectral efficiency.
- •
An FEC code with higher coding gain and no error floor should be preferred for reliability constraint of URLLC. The transmission reliability is determined by error floor free performance below BLER of 10−5. Turbo and LDPC code shows occurrence of error floor for short block lengths around BLER of 10−5. Polar code has error floor free performance shown in Mondelli et al. [16] and Sharma and Salim [18], and hence, it is more reliable than other FEC candidates for desired SNR.
- •
Decoder power consumption is complementary of computational complexity of the decoder. Polar decoders consumed less power due to use of low complexity SC-based decoding (SC and SCL) algorithms [17]. Terminal power consumption in polar code is even 20 times lesser than turbo codes for equivalent complexity.
- •
5. POLAR CODE PERFORMANCE INVESTIGATION FOR URLLC USE CASE: SIMULATION RESULTS AND DISCUSSION
This paper evaluates the performance of polar codes in terms of BLER and SNR (ES/N0), based on some parameters.
Out of all FEC code candidates, turbo and LTE-TBCC code are considered to be unworthy for URLLC scenario, described in 3GPP TSG RAN WG1, R1-1611692 [11], Sharma and Salim [18], Sybis et al. [19] and Onurcan et al. [20]. Thus, the comparative analysis of the polar and LDPC codes for typical range of information block lengths and code rates for NR-URLLC are simulated. Different short block lengths and low code rates have been concerned with QPSK modulation over AWGN and fading channels (with Raleigh distribution, Tapped delay line channel model [TDL-C 300]). Table 1 shows specifications of parameters for URLLC use case.
| Parameters | Specifications | |
|---|---|---|
| Channel coding | LDPC | Polar (PC–CA) |
| Channel | AWGN, fading channel | |
| Modulation | QPSK | |
| Information block length (bits w/o CRC) | 40, 200, 600, 1000 | |
| Code rate | 1/12, 1/6, 1/3 | |
| Decoding algorithm | LOMS (20 iterations) | SCL (L = 8) |
| CRC 24 | CRC 27 | |
Parameter specifications - URLLC scenario
PC–CA polar code design is taken with 27 bits CRC. CA-SCL decoding algorithm with list size L = 8 [11] is considered. LDPC code design Base Graph-2 (BG-2) with Layered Offset Min Sum (LOMS) decoder for 20 iterations is taken for analysis [14].
5.1. Parameters under Consideration
5.1.1. Error performance
Error performance of a code is a main asset that further can define many other performance parameters. In this paper, the error performance is measured in terms of BLER and Eb/N0 for short block information and low code rate as desired for NR-URLLC use case. BLER performance of all candidate coding schemes has been discussed in Sharma and Salim [18]. Among all, only polar and LDPC codes are considered for fair comparison for URLLC applications.
Due to simple code shorting and puncturing mechanisms, the polar code can take the advantage of short block lengths and low code rates. But at the same time, it is hard to design an LDPC code with good BLER performance for short block lengths and low code rates.
For identical performance, the LDPC code requires more number of iterations that means more power consumption, higher computational complexity, lower energy efficiency and hence, higher decoding latency that all are undesirable for URLLC. BLER performance of polar and LDPC codes are compared for interested range of block lengths and code rates over AWGN and fading channels. It is clearly observed in Figures 3–5 that the polar code surpasses LDPC code for all cases considered for URLLC.
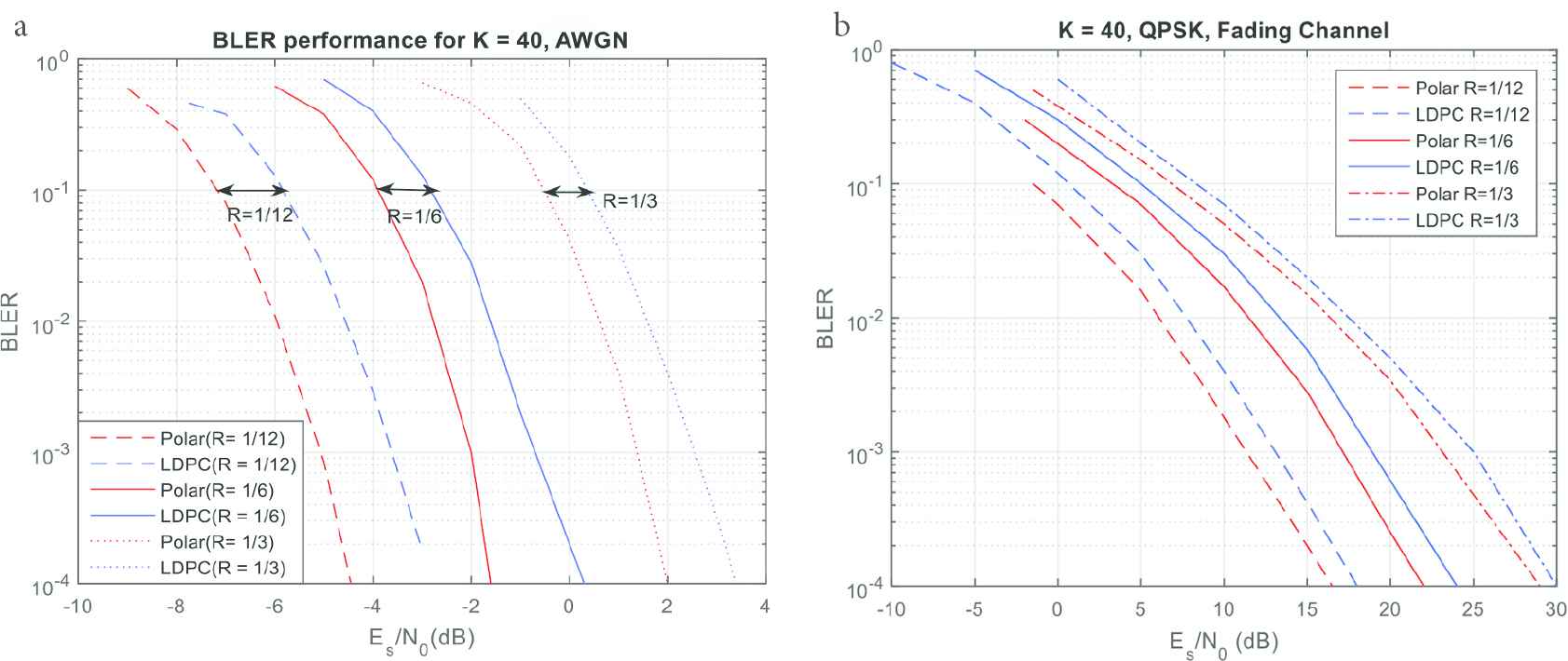
BLER performance comparison for K = 40 over (a) AWGN and (b) fading channels.
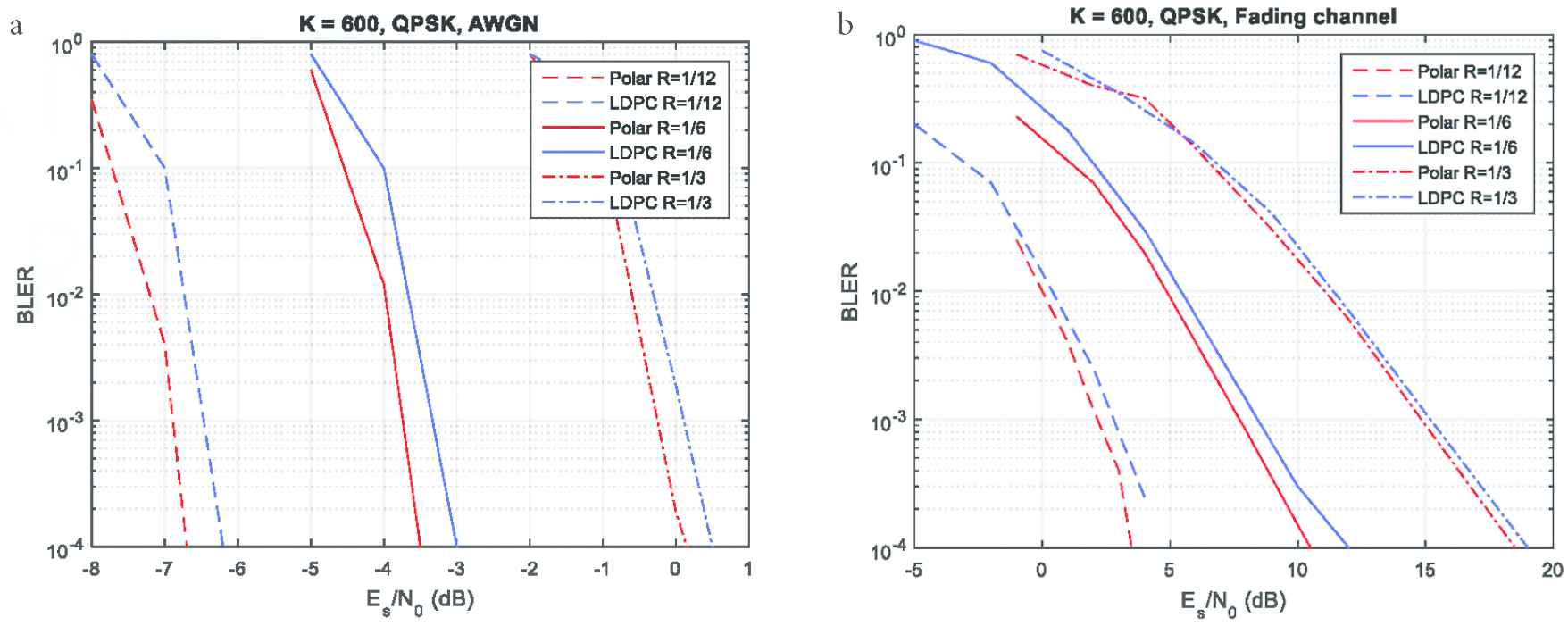
BLER performance comparison for K = 600 over (a) AWGN and (b) fading channels.
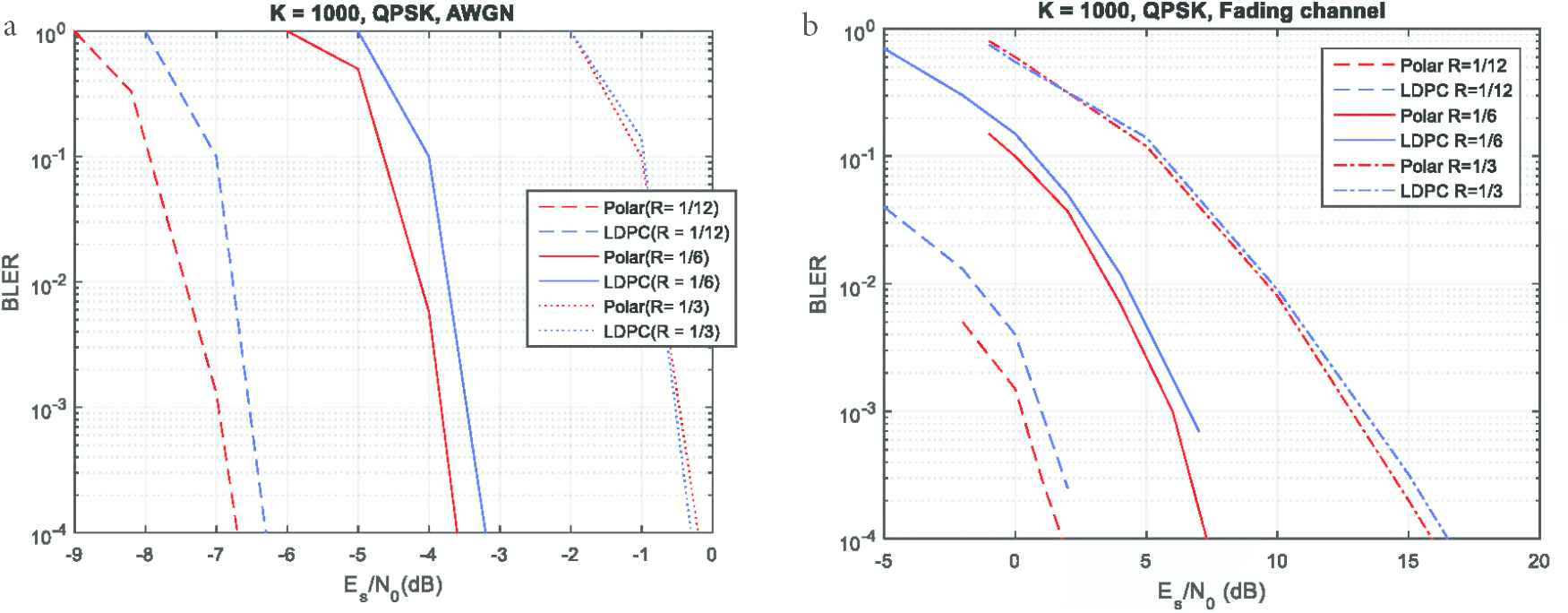
BLER performance comparison for K = 1000 over (a) AWGN and (b) fading channels.
5.1.2. Reliability and error floor
Reliability is one of the very crucial demands of URLLC use case. To obtain reliability of transmission, a channel coding method should be able to support an error floor free BLER performance with high coding gain. For this reason, the analysis is mainly focused on error floor performance and coding gain of polar and LDPC codes to check the reliability constraint. It is obvious from Figure 6 that the LDPC code shows error floor above BLER of 10−5 for K = 200, R = 1/6 and 1/3 over AWGN channel and for R = 1/3 in fading channel. While, the polar code is error floor free for all considered cases. Polar code in Figure 6 is showing better BLER performance with higher coding gain as compared with LDPC codes (in all code rates and at any given SNR). Additionally, from reliability perspective, it is apparent from Figure 6 that the reliability of polar code is higher than that of LDPC code at any given SNR value.
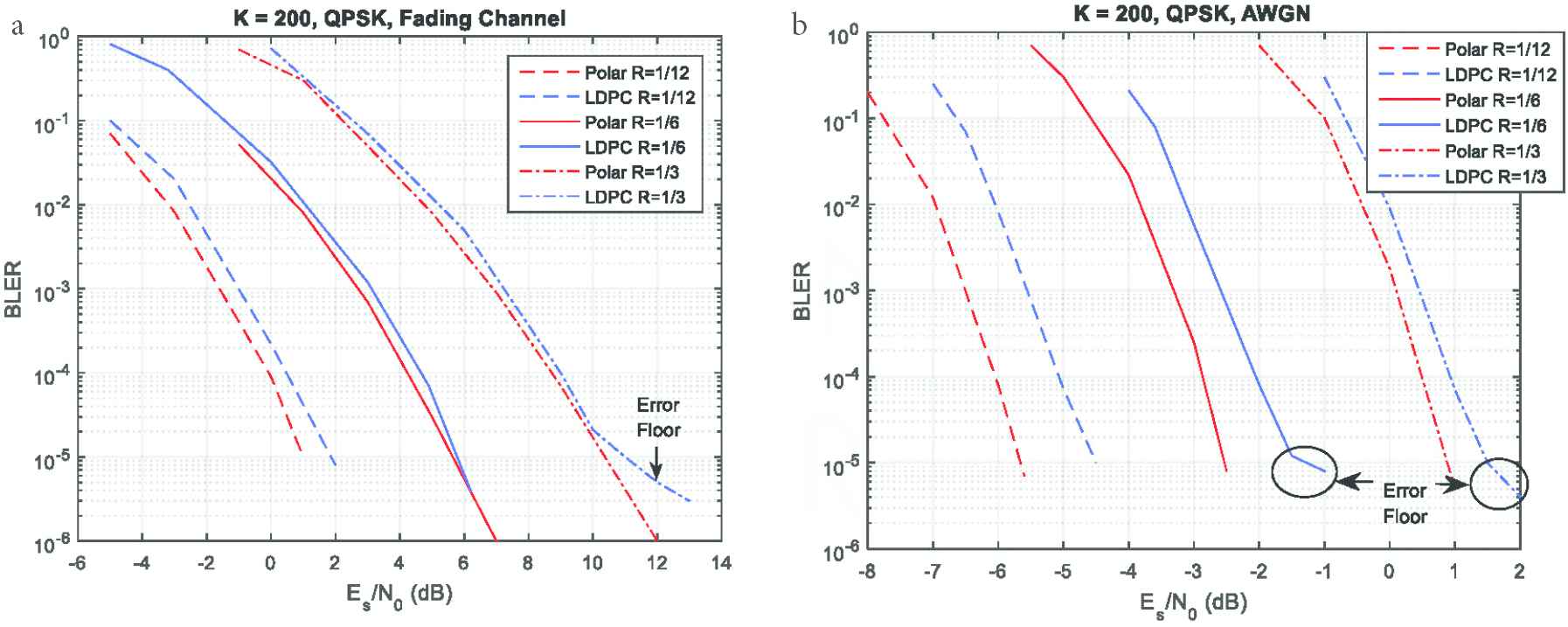
Reliability and error floor comparison of polar and LDPC codes for K = 200 over (a) AWGN and (b) fading channel.
5.1.3. Computational complexity
In general, decoder computational complexity depends on many parameters. However, for any decoding algorithm the computational complexity is highly associated with the decoder power consumption. Also, it is apparent that by lowering the decoder complexity/ power, a code can attain higher energy efficiency. Number of operations needed to decode the information, i.e. the decoder computational complexities of polar and LDPC decoders are evaluated. LOMS decoder with 20 iterations is considered for LDPC code.
While, SCL decoder with moderate list size of 8 (L = 8) is examined for polar decoding. The computational complexity expressions of LDPC-LOMS decoder can be given in Equation (1) [23];
Polar and LDPC codes are compared for computational complexity of different information lengths and at code rate R = 1/3. It is apparent from Figure 7 that the computational complexity of the polar code is lower than that of the LDPC codes for short blocks and low code rates.
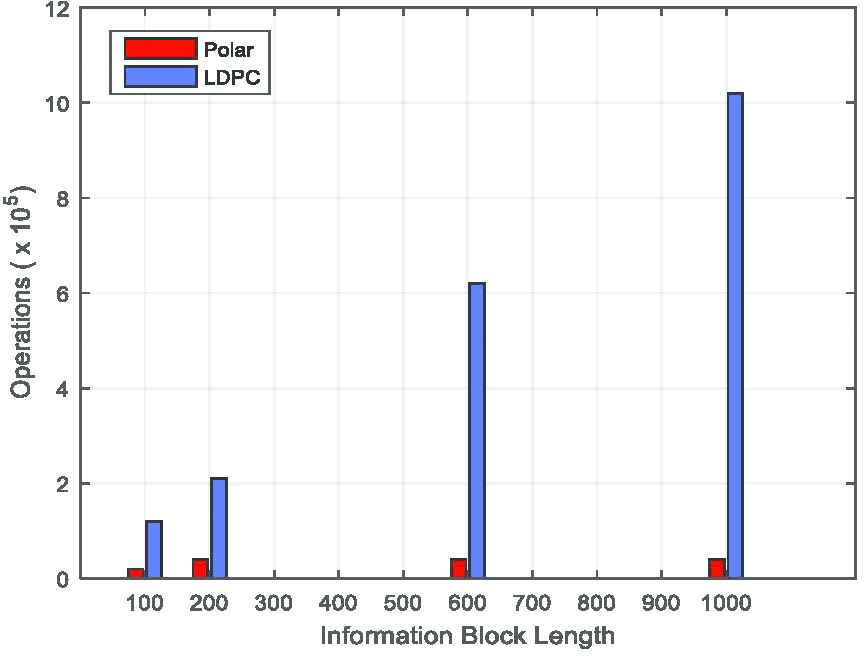
Computational complexity of polar and LDPC codes for R = 1/3.
5.1.4. Decoding latency
Latency is another eminent parameter for performance measurement of URLLC scenario. For time constraint applications the overall latency of 1 ms is demanded for transmission of one packet. The overall latency is mainly comprised of encoding time, channel delay and decoding latency. For 5G-URLLC the self-contained 1-OFDM duration decoding latency is permissible [25].
Although, decoding latency of the polar SC decoder is lower than that of the SCL decoder, SC decoder shows poorer performance as compared with that of SCL decoder. The minimal decoding latency of SC decoder, counted in clock cycle with P parallel processors is given by Equation (3) [25],
While, SCL decoder chooses L best paths from 2L paths that are branching from L most likely previous paths. For this, the path metrics should be sorted to choose the best half and SC decoding should be halted after completion of one round of sorting. Therefore, decoding latency of SCL decoder (in clock cycle) is expressed as Equation (4),
Also, the decoding latency of SCL decoder can be minimized with low value of L but at the cost of performance degradation. So, there is a trade-off between latency and performance of SCL decoders. Decoding latency of PC–CA polar code with SCL decoding (L = 8) is evaluated in Table 2. The maximum code word length Nmax = 4096 is considered thus the decoding latencies of all possible block lengths and code rates are estimated. And, it reaches to the target latency for short block and low code rate as desired in URLLC scenario.
| Information block length (K bits) | 100 | 100 | 100 | 200 | 200 | 600 | 1000 |
|---|---|---|---|---|---|---|---|
| Code word length (N) | 512 | 1024 | 2048 | 1024 | 2048 | 2048 | 4096 |
| Code rate (R) | 1/3 | 1/6 | 1/12 | 1/3 | 1/6 | 1/3 | 1/3 |
| Decoding latency (μs) | 0.51 | 0.89 | 1.52 | 1.19 | 1.78 | 2.45 | 3.71 |
Estimates for polar code decoding latency
6. CONCLUSION
Polar code is an acclaimed research in channel coding area and get chance to enter in the FEC code candidacy race for 5G. Moreover, polar code is appointed as control channel coding method for 5G-eMBB use case and over PBCH. In this paper, various channel coding candidates for 5G-URLLC scenario are discussed. Based on the discussion, only suitable channel codes are compared for this use case. To fulfil the needs for ultra-high reliability and low latency, the error floor free performance with short information block lengths and low coding rates are considered. Polar and LDPC codes are compared on the basis of BLER performance, reliability, error floor, decoding complexity and latency. It is observed through simulations that BLER performance of polar code surpasses that of LDPC code for short block lengths and low code rates. Also, it is proved that polar code is error floor free and more reliable than LDPC code at any given SNR. Decoder complexity is also discussed and it is found that Polar-SCL decoder complexity is lower than that of LDPC-LOMS decoder for typical range of block lengths and code rates desired for 5G-URLLC scenario. Also, this paper depicts that the low decoding latency demands of URLLC use case are fulfilled by polar code. Therefore, polar code is considered as a most efficient and suitable contender for 5G-URLLC scenario.
REFERENCES
Cite this article
TY - JOUR AU - Arti Sharma AU - Mohammad Salim PY - 2019 DA - 2019/07/23 TI - Polar Code Appropriateness for Ultra-Reliable and Low-Latency Use Cases of 5G Systems JO - International Journal of Networked and Distributed Computing SP - 93 EP - 99 VL - 7 IS - 3 SN - 2211-7946 UR - https://doi.org/10.2991/ijndc.k.190702.005 DO - 10.2991/ijndc.k.190702.005 ID - Sharma2019 ER -
