Utilizing Type-2 Fuzzy Sets as an Alternative Approach for Valuing Military Information
- DOI
- 10.2991/ijndc.k.190710.004How to use a DOI?
- Keywords
- Type-2 fuzzy sets; knowledge engineering; value of information; decision support
- Abstract
Knowledge elicitation from a group versus a single source typically yields outcomes that range in agreement and promote a level of uncertainty. Recently, the use of Type-2 fuzzy sets has been proffered as an alternative approach for capturing the difference of opinions expressed by a group of experts during the knowledge elicitation process. This paper examines the preliminary results associated with the transition of an existing Type-1 fuzzy set decision support system to a more flexible Interval Type-2 fuzzy approach.
- Copyright
- © 2019 The Authors. Published by Atlantis Press SARL.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
Within current military environments, the volume, velocity and variety of available information has exploded as compared with past eras. The increase in data while potentially advantageous, creates challenges for how to process that data in meaningful ways. As a result, it is increasingly likely that military commanders and their staffs have access to more information than they can use in a timely manner. This situation highlights the classic information overload problem. In battlefield situations, the issue of deciding which information is most relevant is critical to mission success. For the military, this problem is further aggravated by the restricted time constraints central to the military decision making cycle.
Given the vast amount of information, military intelligence analysts are continually challenged with combing through the material to judge which information is most important for the current situational context. Calculating this “Value of Information (VoI)” metric is non-trivial; in fact, it is a highly complex, multi-step task exacerbated by the wide range of information types and military situational contexts [1].
Over the past several years, work has been completed to prototype an automated VoI decision support tool for military intelligence analysts [2,3]. This system was constructed using a fuzzy logic-based computational intelligence approach, where knowledge elicitation techniques were used to gather information from experts to construct the fuzzy rules [4]. Fuzzy systems are known to be excellent for reasoning where information is uncertain, incomplete, imprecise, and/or vague [5–9]. The system was constructed using the typical Type-1 fuzzy sets introduced by Zadeh [8].
Recently, the use of Type-2 fuzzy sets has been proffered as an alternative approach for capturing the difference of opinions expressed by a group of experts during the knowledge elicitation process. The work described in this paper examines the preliminary results associated with transitioning an existing Type-1 fuzzy set decision support system with a more flexible Interval Type-2 (IT2) fuzzy approach. The remainder of the paper is organized as follows: first, the motivational and background information on the current Type-1 Fuzzy VoI system is presented in Section 2. In Section 3, Type-2 Fuzzy Sets are briefly introduced followed by the preliminary results associated with converting from the Type-1 to the Type-2 approach. Concluding remarks and future directions are given in Section 5.
2. BACKGROUND
This section provides background information to motivate and understand the military information evaluation process and the need and use of the prototype VoI system. First, the concept of rating individual pieces of information in a military context is explained. This is followed by a brief discussion of the architecture, development, and extensions related to the VoI system. Finally, the knowledge elicitation process used to ascertain the fuzzy rules in the prototype system is reviewed.
2.1. Evaluating Information
The only military regulatory guidance describing how to rate information, as well as requiring such a rating, is contained in the annex to North Atlantic Treaty Organization Standard Agreement 2022 and repeated in Appendix B of US Army Field Manual FM-2-22.3 [10,11]. Each piece of information is to be judged by combining assessments based on the reliability of the source and its information credibility or content. The Source Reliability (SR) value comes from the range (high to low): {reliable, usually reliable, fairly reliable, not usually reliable, unreliable, cannot judge}. The Information Content (IC) choices are (high to low): {confirmed, probably true, possibly true, doubtfully true, improbable, cannot judge}.
Note that there is no doctrinal guidance on how the ratings for a piece of information (e.g. SR = fairly reliable; IC = probably true) are to be combined, utilized or interpreted. Further, there is no direction on how individual or composite ratings should be treated with respect to various mission contexts. Also, it is clear that using only SR and IC is probably insufficient to determine a reasonable “value” for a piece of information. Discussions among the researchers and with military intelligence subject matter experts led to the addition of information timeliness and mission context in the VoI determination process [4].
2.2. VoI System
It is interesting to note that the labels within the source reliability and information content domains are words, not numbers. These linguistic variables represent degrees of confidence and make fuzzy logic an appropriate choice for the VoI computations [12].
A Fuzzy Associative Memory (FAM) model was chosen to construct the prototype VoI system. A FAM is a multi-dimensional table where each dimension corresponds to one of the input domains. Fuzzy if-then rules are then represented in the FAM; the inputs (rule antecedents) are used as indices to access the appropriate “cell” of the FAM, and the value in the cell represents the output (rule consequent). A fuzzy rule with two antecedents has the form “If X is A and Y is B then Z is C” where A and B are fuzzy sets over the two input domains and C is a fuzzy set over the output domain.
In the prototype VoI system, three inputs are used: source reliability, information content, and timeliness; the concept of various mission contexts is accounted for by having multiple models. The output of the model is the VoI metric.
The overall architecture of the prototype fuzzy system is shown in Figure 1. Instead of using one 3-dimensional FAM, two 2-dimensional FAMs were used. The reasoning behind this decision was presented in detail in Hammell II et al. [2], but essentially it provided a simpler knowledge elicitation process for the Subject Matter Experts (SMEs), decreased the total number of fuzzy rules, and provided a potential for the output of the first FAM to be useful on its own.
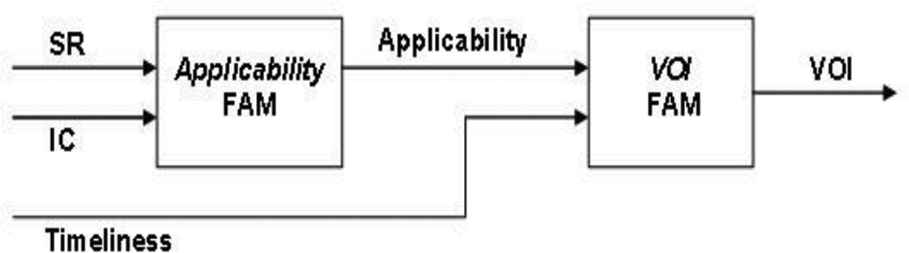
VoI prototype system architecture [3]. VoI, value of information; FAM, fuzzy associative memory; SR, source reliability; IC, information content.
As seen in Figure 1, two inputs feed into the Applicability FAM: SR and IC; the output of the FAM is termed the information applicability decision. Likewise, two inputs feed into the VoI FAM: one of these (information applicability) is the output of the first FAM while the other input is the information timeliness value. The output of the second FAM, and the overall system output, is the VoI metric. Different mission contexts are represented by having multiple, automatically selected VoI FAMs.
The fuzzy rules represented in the FAMs capture the relationships between the input and output domains. For example, an actual rule in the Applicability FAM might be: “if Source Reliability is ‘Usually Reliable’ and Information Content is ‘Probably True’, then Information Applicability is ‘Highly Applicable’.” Knowledge elicitation from military intelligence SMEs was used to construct the fuzzy rules [4].
Within the Applicability FAM, the two input domains (source reliability and information content) are divided into five fuzzy sets following the guidance provided in US Army Field Manual FM-2-22.3 [10]. The omission of the “cannot judge” category from both input domains is explained in Hammell II et al. [2]. Decomposition of the other domains was driven by the SMEs. The timeliness input domain was decomposed into three fuzzy sets (recent, somewhat recent, and old). The “information applicability” output domain was decomposed into nine fuzzy sets (ranging from not applicable to extremely applicable) while the VoI output domain utilized 11 fuzzy sets (ranging from not valuable to extremely valuable).
The decomposition of the information content domain into its five fuzzy sets is shown in Figure 2. Each element in the domain has some grade of membership, from 0 to 1 inclusive, in each fuzzy set in the domain. The membership function determines the grade of membership; the shape of the fuzzy sets determines the membership function.
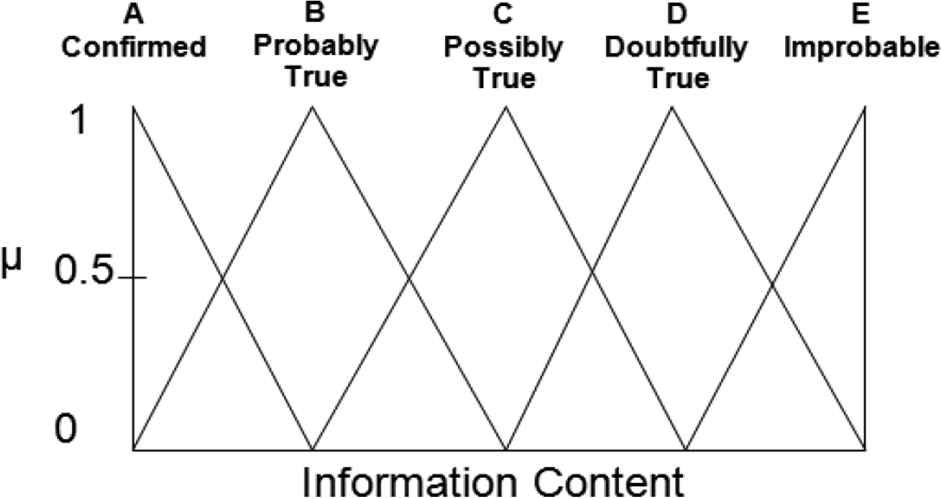
Information content fuzzy membership diagram.
In Figure 2, the membership value is shown on the y-axis and the values contained within the domain are shown on the x-axis (at the top). The illustrated decomposition requires the membership functions to be isosceles triangles with bases of the same width. The decompositions for all domains in the VoI system follow this requirement. Thus, any input within a domain will belong to at most two fuzzy sets; that is, any input will have non-zero membership in no more than two fuzzy sets. This means that, for each input, the antecedents for at most two fuzzy rules associated with that domain will be satisfied. Furthermore, the sum for all membership values in the sets to which any input belongs will be equal to 1.
Note that, in general, the shape of the fuzzy sets in a fuzzy system does not have to be triangular as shown in Figure 2. Also, the fuzzy sets decomposing a domain do not have to overlap in a regular pattern, nor does the sum have to be 1 for membership values for all sets in which an element is a member. Examination of other types of membership functions as applied to the VoI system can be found in Hanratty et al. [13] and Miao et al. [14].
The output from the system is determined by the standard centroid defuzzification strategy. That is, the degree to which each rule influences the overall output is directly related to the degree to which its inputs match its antecedent fuzzy sets. Following the above decomposition requirements for a 2-dimensional FAM structure, at most four fuzzy rules will have non-zero degrees (two rules will have “x” antecedents satisfied by input x and two rules will have “y” antecedents satisfied by input y; their intersection in the FAM defines the four fuzzy rules that should be “fired”). This aspect, plus the fact that the degrees for all rules will add to one, allows the decomposition structure to provide a computationally efficient defuzzification process.
More detailed descriptions of the FAMs, the fuzzy rule bases, the domain decompositions, and other implementation aspects of the system can be found in Hanratty et al. [3]. With the understanding that complex military decisions rarely rely on a single piece of information, the current (phase 2) prototype extends the original VoI calculation from a single element of information to an amalgamation of multiple elements of information that either complement or contradict the original premise [15]. The VoI prototype systems, the initial version and phase 2, have been demonstrated to SMEs. Both versions of the prototype and its output have met SME expectations [16].
2.3. Knowledge Elicitation
Construction of any knowledge-based system originates with the collecting and organizing of domain specific expertise. For the VoI initiative this meant eliciting knowledge from a group of military intelligence SMEs. In order to capture the cognitive requirements necessary to refine the model and build the fuzzy rules, the team adopted the conceptual method of knowledge elicitation introduced by Cooke [17]. The goal of the conceptual method is to derive the concepts and their associated inter-relationships within the domain. Steps within the method include: (1) discovering relevant concepts, perhaps through interviews; (2) gathering opinions from one or more SMEs as to how the concepts relate; (3) representing the relationships; and (4) interpreting the result.
To capture the concepts and inter-relationships, a series of interviews and two Likert surveys were performed over a period of several months. The input was elicited from a diverse group of military analysts assigned to the research laboratory. The focus of the first survey was capturing the generic information applicability rating associated with the military doctrinal information rating model described above; comparing and contrasting the source reliability to the information content. The composite rating was expressed on a Likert scale of one through nine with one being least applicable and nine being extremely applicable to military missions.
Using the results from the newly derived Information Applicability Survey, the second survey focused on the SMEs assigning a Likert scale from zero through 10 for the VoI under three military operational tempos with varying information latencies. A thorough review of the knowledge elicitation process used with SMEs to develop the concepts, inter-relationships, cognitive requirements, collect functional requirements, and elicit the fuzzy rules is presented in Hanratty et al. [4]. Noteworthy, although a consensus was reached by the SMEs with respect to the development of the final inference rules, seldom were the individual interpretations of the antecedents and associated consequence in total agreement. For example, it was not unusual for the SMEs to derive consequences on the Likert surveys with ranges varying across three levels (e.g. 1, 3 and 5). In addition, it was common for the SMEs to have varying understandings of the linguistic concepts that were developed. These facts reaffirmed the notion that military science is as much an art as it is a science and encouraged the team to examine Type-2 fuzzy sets as an alternative approach for reasoning with uncertainty.
3. TYPE-2 FUZZY SETS
Zadeh [8,12] introduced fuzzy sets in 1965 and then proposed Type-2 fuzzy sets in 1975. Thus, after 1975 the original fuzzy sets became known as Type-1 fuzzy sets. Even though Type-2 fuzzy sets have existed for nearly as long as Type-1 fuzzy sets, Type-2 fuzzy sets were initially not used in applications as much as their Type-1 counterparts. This began to change around 2000 when Mendel [18–21] began to popularize their usage through his work.
While Type-1 fuzzy sets have long been used to account for uncertainties in data and information [12] they have been criticized for their inability to handle uncertainties that come from (1) different words having different meanings to different people; (2) difference in opinions among experts with respect to the design of fuzzy rules in fuzzy systems; (3) only having noisy training data; and (4) having noise associated with the measurement of the inputs to fuzzy systems [22]. Type-2 fuzzy sets have been shown to be capable of accounting for these uncertainties [22]. The fuzzy sets shown in the decomposition of the information content input domain in Figure 2 are all Type-1 fuzzy sets. The endpoints of each triangle (fuzzy set) are crisp; i.e., the left and right endpoints of each fuzzy set are denoted by one specific value.
Figure 3 presents an IT2 fuzzy set; these sets use intervals as membership values [18,23]. Such sets are useful in circumstances where it is difficult to allocate an exact membership grade for each element in the fuzzy set [23]. In Type-2 fuzzy sets, the precise membership value is contained within the given interval. As Figure 3 illustrates, the endpoints for each leg of the triangle are denoted as a range versus as a single value.
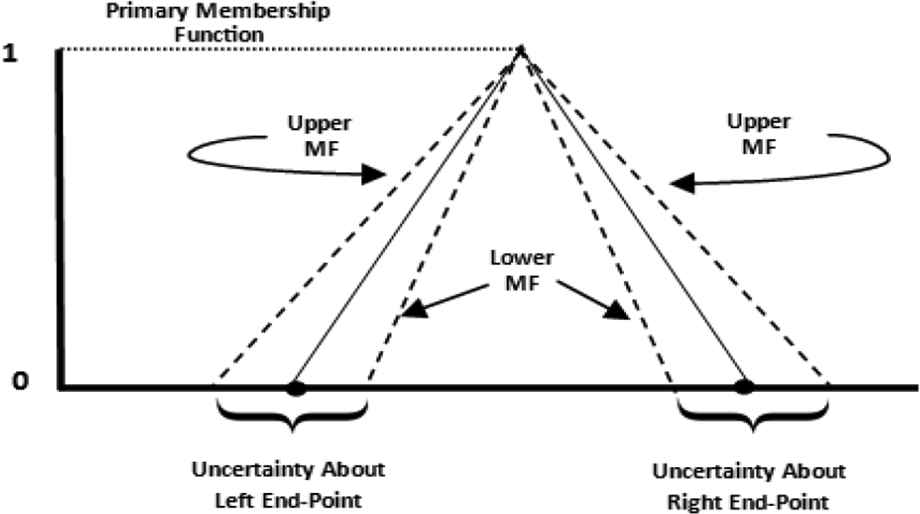
Interval Type-2 fuzzy set [21]. MF, membership functions.
The range associated with each endpoint reflects the uncertainty that arises from one or more of the situations previously mentioned in this section. For each leg of the triangle, the upper and lower Membership Functions (MF) provide a bound on the region of uncertainty; this area is called the Footprint of Uncertainty (FOU) [24]. Note that if all uncertainty about the endpoints is removed then only the triangle represented by the solid line in Figure 3 remains. Thus, an IT2 fuzzy set reduces to a Type-1 fuzzy set in the absence of uncertainty about the definition (membership values) of the fuzzy set [25].
When IT2 fuzzy sets are used within a fuzzy system the inference process requires an additional step to produce the required crisp output. This extra step involves the type reduction of the Type-2 fuzzy set to a Type-1 fuzzy set [25]. Historically, this type reduction involves the computation of the centroid of the Type-2 fuzzy set which is then represented as a Type-1 fuzzy set; the type-reduced set is then defuzzified to produce the final crisp output. Several common type reduction methods along with their advantages and disadvantages are presented in Abeulenin [26].
4. TYPE-2 PRELIMINARY RESULTS
This section presents the conversion and early discussion of an IT2 Fuzzy Model (FM) built from the original VoI prototype. The system was developed using MATLAB’s fuzzy logic toolkit and an open source IT2 extension by Taskin and Kumbasar [27].
4.1. Type-2 Fuzzy Conversion
The first step in converting the original Type-1 VoI system to a Type-2 system was to determine which concepts held the biggest uncertainty. That is, what concepts held the greatest variability in understanding between the SMEs. Toward this end, it was decided that the linguistic ambiguity associated with antecedental concepts held potentially the biggest payoff. Therefore the fuzzy membership associated with information content {confirmed, probably true, possibly true, doubtfully true, improbable}, source reliability {reliable, usually reliable, fairly reliable, not usually reliable, unreliable} and applicability {extremely, highly, moderately, somewhat, not} were modified by extending the endpoints with a range of possibility. In this instantiation the endpoints were extended by ±12.5%. Figure 4 depicts an example of the Type-2 fuzzy extension for the information content membership functions. The endpoints are defined by an upper and lower bound presented with the dotted-lines. Similar instantiation were performed for source reliability and applicability membership functions.
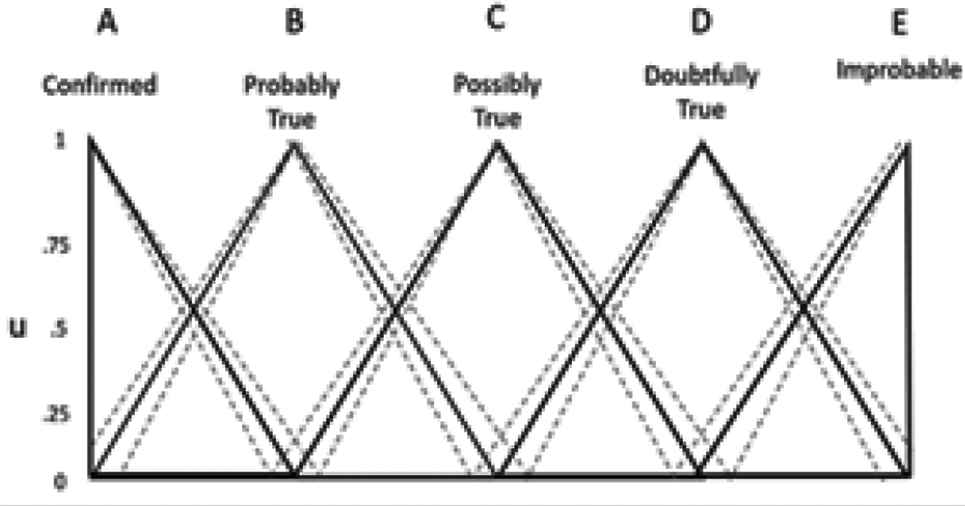
Interval Type-2 fuzzy set [21]. MF, membership functions.
4.2. Interval Type-2 Fuzzy System
With the new IT2 representations defined for the VoI antecedental concepts, it is useful to visualize the implied difference that “fuzzifying” the endpoints has on the fuzzy inference. Figure 5 depicts a comparison of Type-1 versus IT2 where the Z-axis represents the fuzzy membership result [28]. Note that with identical input (P) the typical Type-1 representation yields a single fuzzy membership point, while with the IT2 representation, the same input (P) yield a range of results – itself a fuzzy membership.
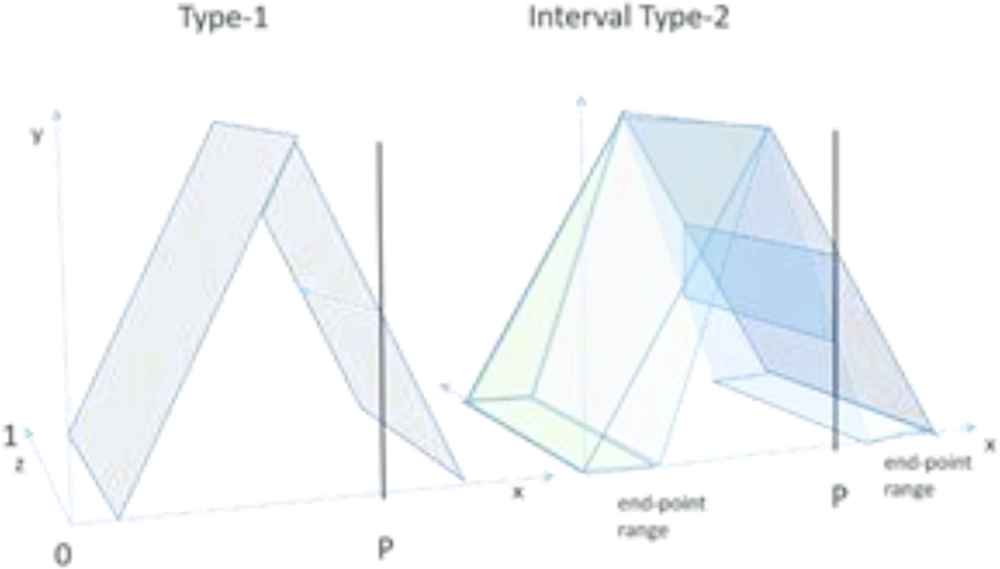
Type-1 vs interval Type-2 diagram comparison [28].
It is the addition of the extra IT2 fuzzy set that necessitates an extra step in an IT2 fuzzy system. This extra step involves the type reduction of the Type-2 fuzzy set to a Type-1 fuzzy set. The most popular type reduction is called the Karnik–Menel (KM) algorithms [25].
At a high-level of abstraction, the KM algorithm involves the execution of two independent procedures: calculating the centroid for the composite upper and lower halves of the IT2. The results are combined with either a fuzzy min or prod function. A pictorial representation of the KM process is shown in Figure 6. A full explanation of the KM algorithm is found in Karnik and Mendel [29] and Mendel [30].
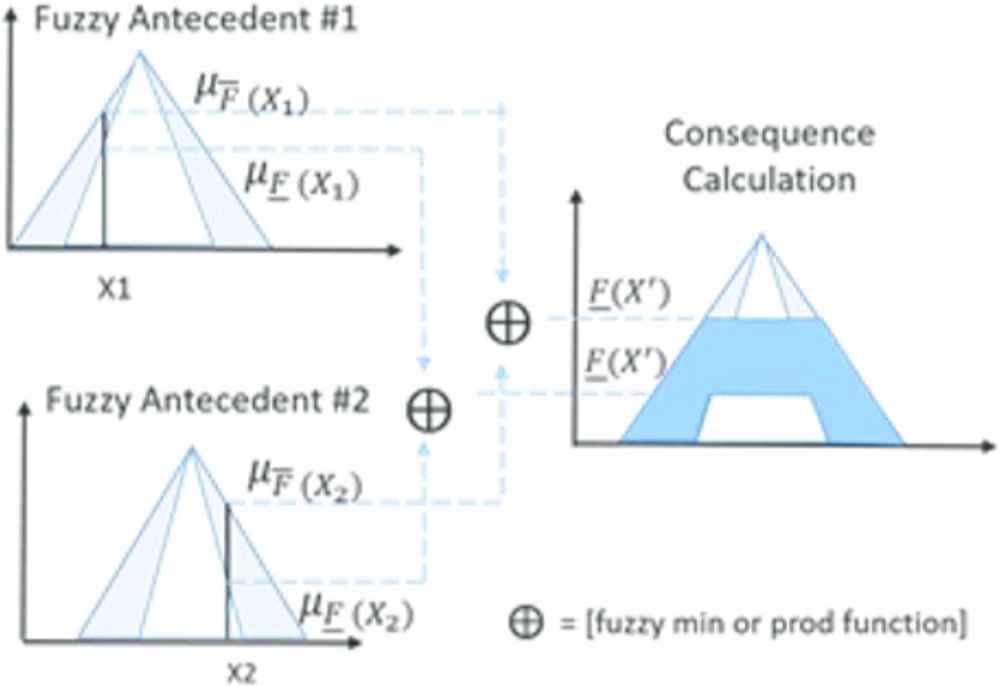
KM algorithm pictorial overview [25]. KM, Karnik–Menel.
4.3. VoI Type-1 vs Type2 Preliminary Comparison
This section explores the different outputs associated with the original Type-1 VoI fuzzy system to that of the prototyped IT2 VoI fuzzy system.
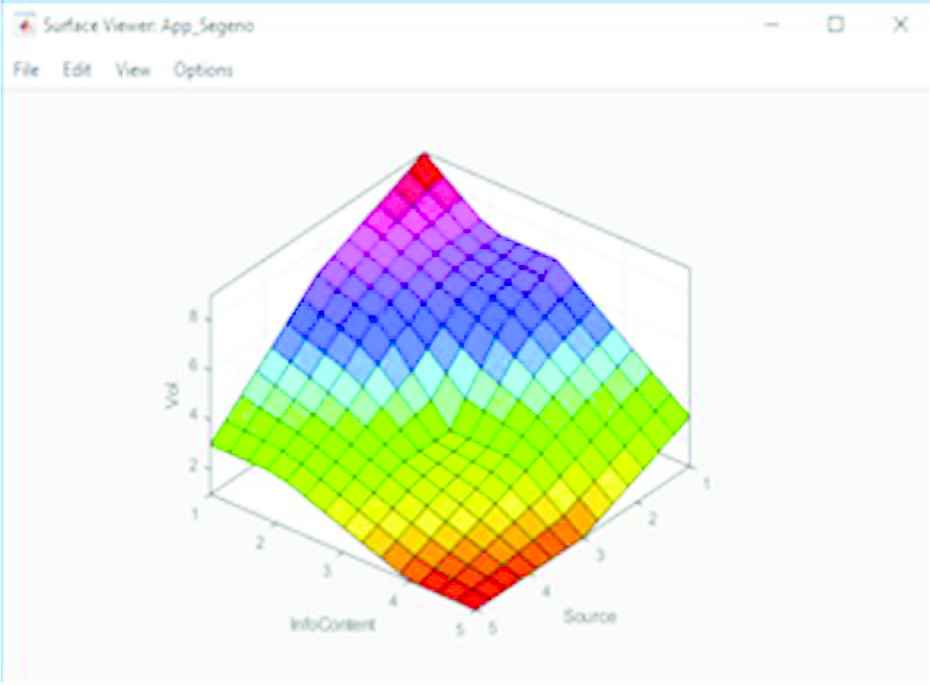
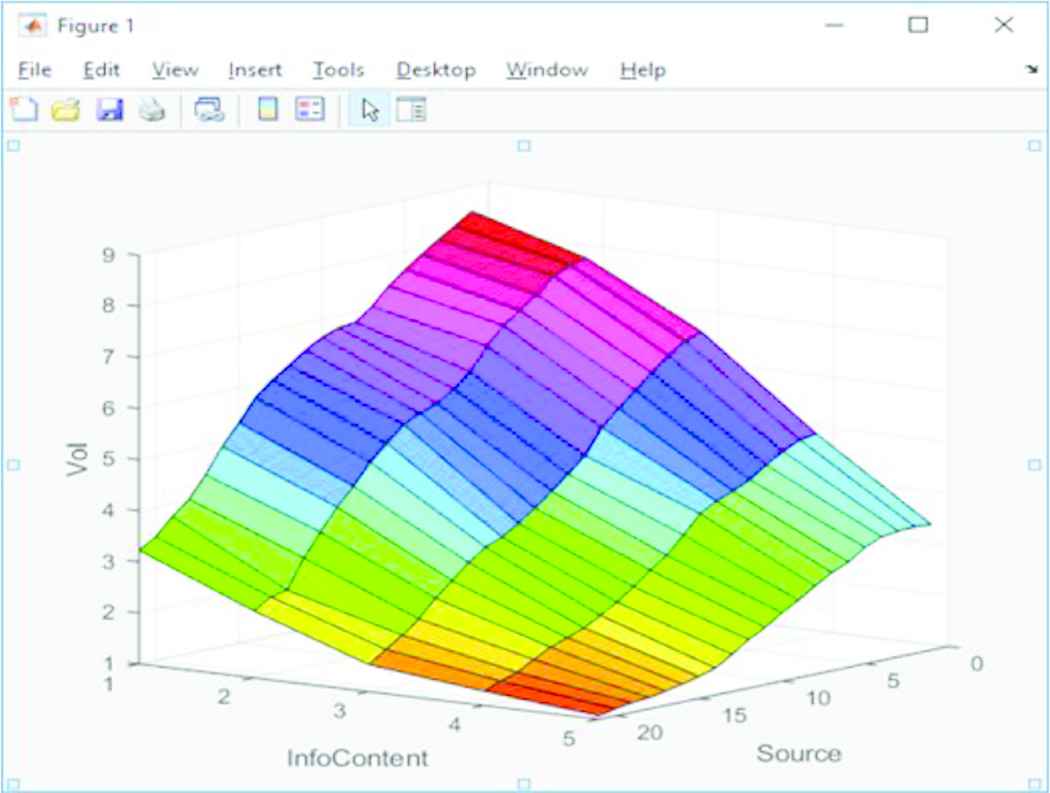
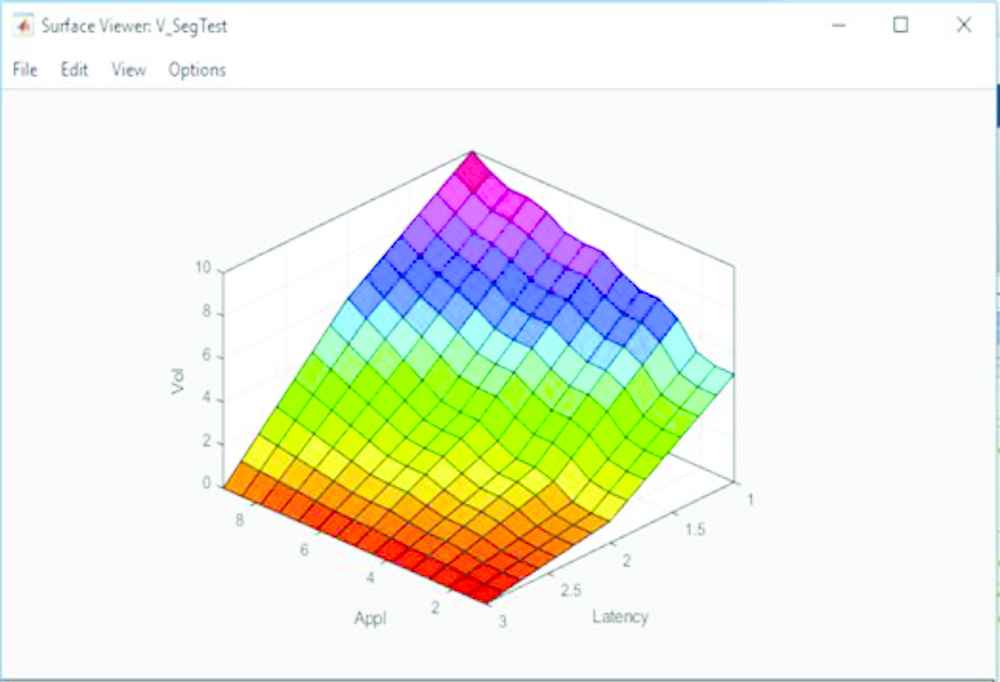
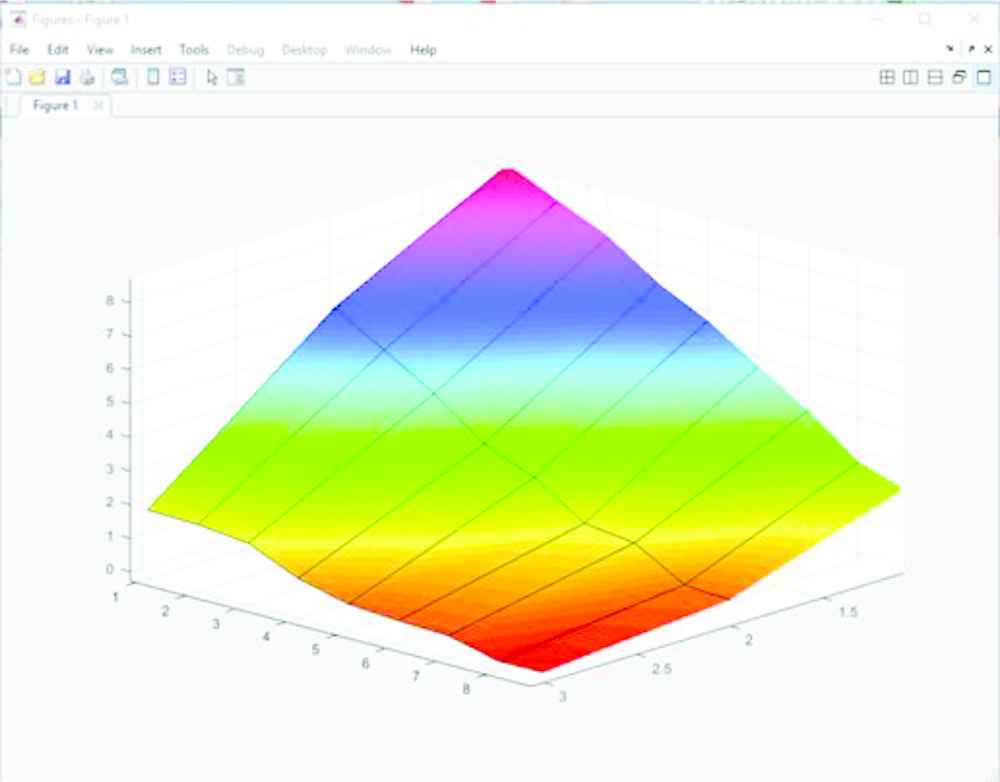
The first comparison made is between the outputs associated with the Applicability FAMs. Surface Plots for the original Type-1 and prototype IT2 Applicability FAMs are shown in Figures 7 and 8, respectively. On first glance there appears to be little difference; both plots generally incline upwards and share the same features.
Type-1 applicability FAM surface plot. FAM, fuzzy associative memory.
Type-2 applicability FAM surface plot. FAM, fuzzy associative memory.
It is not until one looks at the actual scores that a difference is noted. Shown in Tables 1 and 2 are the numerical results associated with the original Type-1 and Type-2 Applicability FAMs respectively. Comparing the numbers, one can quickly see an “absorption effect” that the IT2 has on the fuzzy calculations. Reworded, IT2 cell calculations are profoundly influenced by the result of their nearest neighbor. For example, the number associated with the cell C3 (3) in the original FAM absorbs the relationship with B2, B3 and C2 becoming 3.91 in the IT2 FAM. The absorption effect is attributed to the end-point expansion of the SR and IC concepts in the IT2 version.
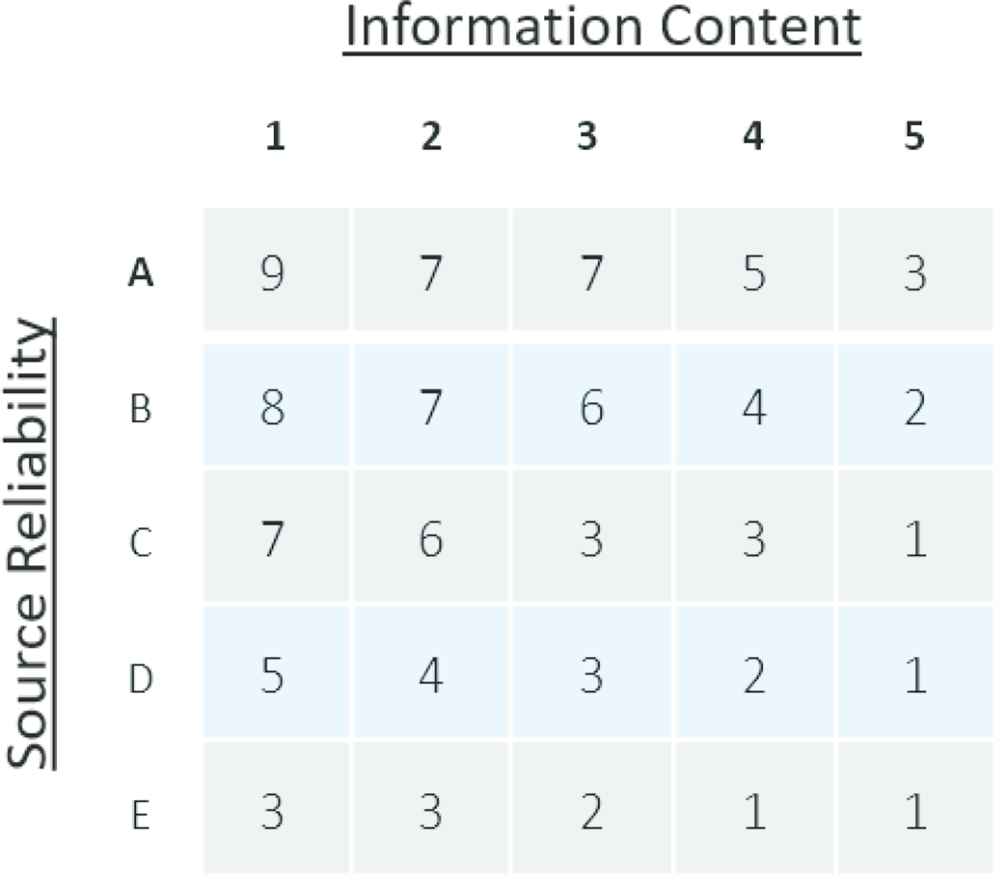 |
Original Type-1 applicability FAM
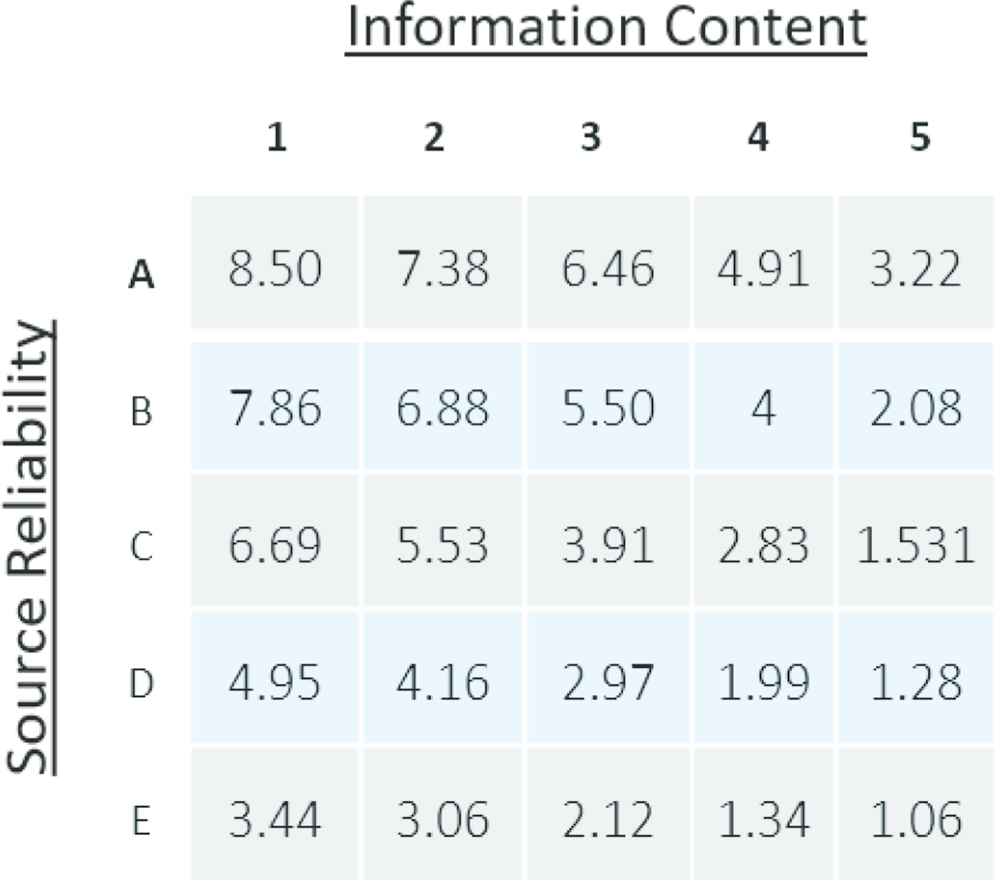 |
Type-2 applicability FAM
Similar to the Applicability FAM, the results obtained when examining the differences between the Type-1 and Type-2 VoI FAMs follow a similar pattern. While only subtle differences are noted when comparing the surface plots in Figures 9 and 10, the actual numbers reveal a slightly different result. Shown in Table 3 are the numerical results associated with the original Type-1 and Type-2 VoI FAMs. Once again, one can see the “absorption effect” that the IT2 has on the fuzzy calculations. While subtle, the range of change is from ±0.4 Likert points, which when combined equals a shift of one Likert position in value.
Type-1 VoI FAM surface plot. VoI, value of information; FAM, fuzzy associative memory.
Type-2 VoI FAM surface plot. VoI, value of information; FAM, fuzzy associative memory.
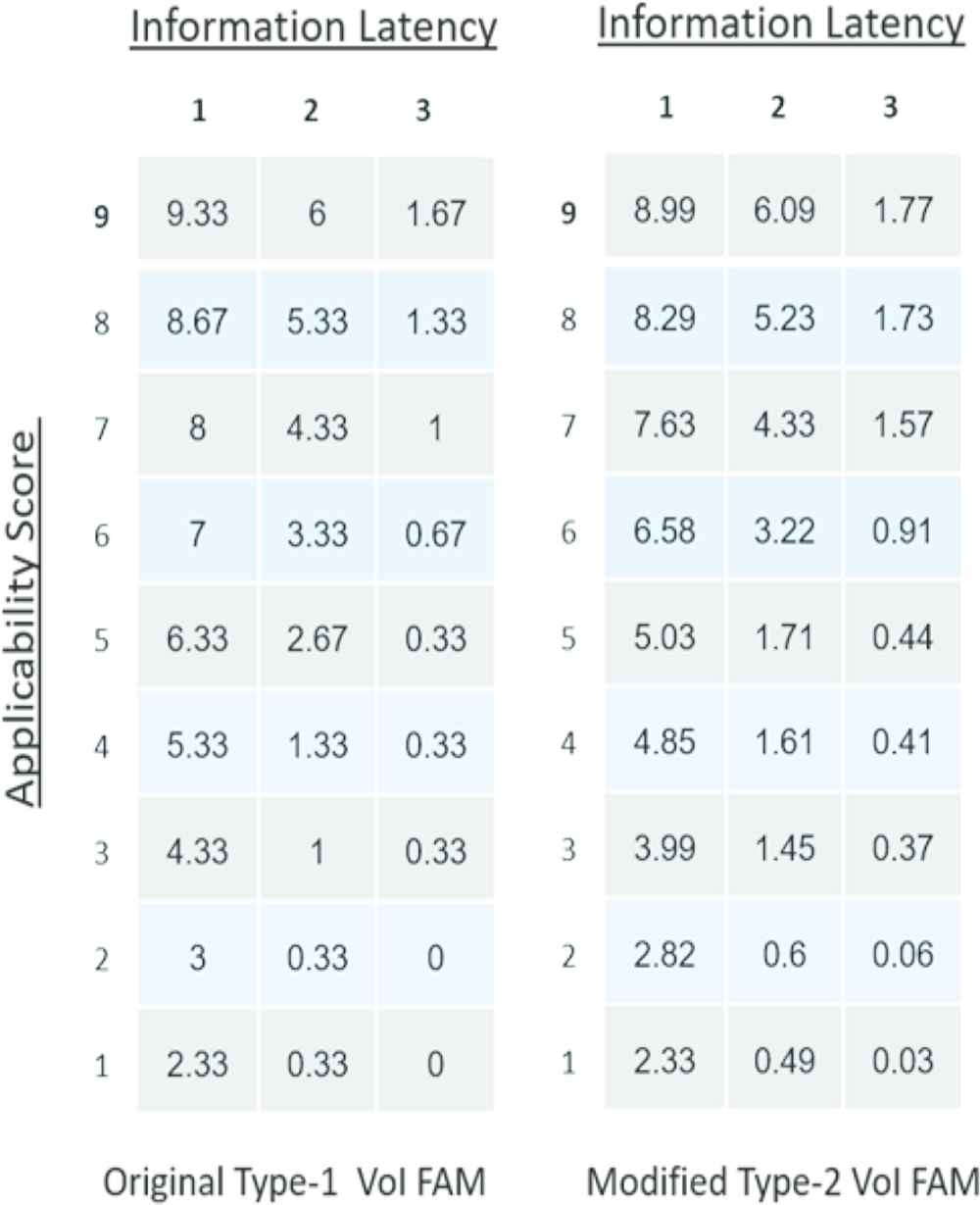 |
VoI FAM comparison
A final comparison can be made from the results obtained when each system is run in its entirety. Table 4 depicts the results of the original Type-1 VoI system (Type-1) compared with the new IT2 VoI system (Type-2) for nine inputs where Source Reliability = 1.5, 2.5 and 3.5; Information Content = 1.5, 2.5 and 3.5; with Information Timeliness held constant at 1.5.
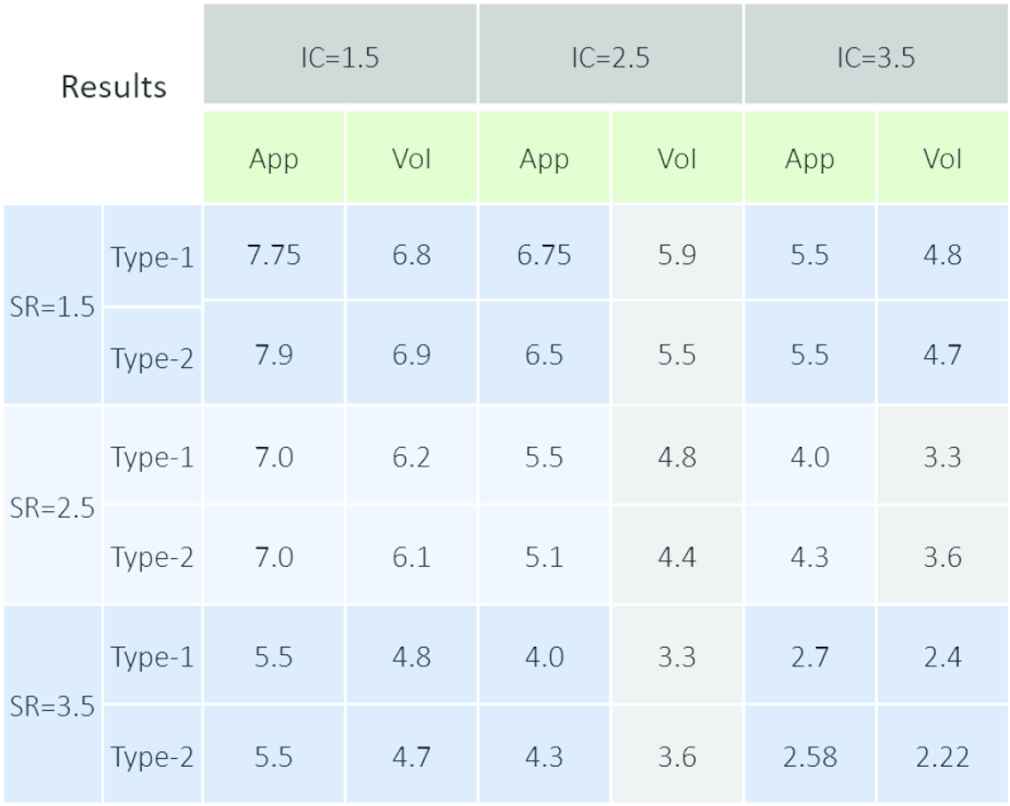 |
System level VoI Type-1 vs Type-2 results
Differences in VoI calculations ranged from 0.1 to 0.4 Likert points. The biggest delta was observed when the IC input was 2.5 (between probable and possible) and to a lesser degree at an IC was 3.5 (between possible and doubtful). Interestingly six of the VoI measures were lower with the IT2 calculation as compared with the Type-1 measures.
5. CONCLUSION AND FUTURE WORK
Knowledge-based systems that rely on the elicitation of domain information from a group of individuals versus a single source typically yield results that range in agreement and promote a level of system uncertainty. Recently, the use of Type-2 fuzzy sets has been offered as an alternative to account for the differing opinions expressed by the experts during the knowledge elicitation process. With that understanding, this paper presented the preliminary results in an effort to transition an existing Type-1 fuzzy system with an IT2 fuzzy approach.
While much works remains to be done, the early results reveal a couple of interesting observations. First, at a high-level the transition from Type-1 to Type-2 is relatively straightforward; decide on the spread of your membership curves and move forward. The challenge however is finding membership spreads that correlate with your SMEs. Second, on a macro-level “fuzzifying” the antecedental endpoints yielded little change, however on a micro-level an “absorption effect” was observed, where individual IT2 cell calculations were profoundly influenced by the results of their nearest neighbor.
Looking forward the next obvious step for this effort is to validate of the IT2 system by producing a comprehensive, statistically-relevant human-in-the-loop experiment to compare the output with that of SMEs. Additionally, there are plans to investigate alternative type reduction algorithms and compare approaches. At last, there is interest in exploring the notion of using the Type-2 information as a surrogate information granule and explore how it might be used in a granular computing reasoning strategy [31,32].
REFERENCES
Cite this article
TY - JOUR AU - Timothy P Hanratty AU - Robert J Hammell PY - 2019 DA - 2019/07/23 TI - Utilizing Type-2 Fuzzy Sets as an Alternative Approach for Valuing Military Information JO - International Journal of Networked and Distributed Computing SP - 133 EP - 139 VL - 7 IS - 3 SN - 2211-7946 UR - https://doi.org/10.2991/ijndc.k.190710.004 DO - 10.2991/ijndc.k.190710.004 ID - Hanratty2019 ER -
