Journal of Nonlinear Mathematical Physics

<Previous Article In Issue
Download article (PDF)
Next Article In Issue>
Volume 27, Issue 1, October 2019, Pages 17 - 35

Multicomplex solitons

Authors
Julia Cen
Department of Mathematics, City, University of London Northampton Square, London EC1V 0HB, UK,julia.cen.1@city.ac.uk
Andreas Fring
Department of Mathematics, City, University of London Northampton Square, London EC1V 0HB, UK,a.fring@city.ac.uk
Received 7 December 2018, Accepted 11 June 2019, Available Online 25 October 2019.
DOI
10.1080/14029251.2020.1683963How to use a DOI?
Keywords
nonlinear wave equations; solitons; quaternions; coquaternions; octonions
Abstract

We discuss integrable extensions of real nonlinear wave equations with multi-soliton solutions, to their bicomplex, quaternionic, coquaternionic and octonionic versions. In particular, we investigate these variants for the local and nonlocal Korteweg-de Vries equation and elaborate on how multi-soliton solutions with various types of novel qualitative behaviour can be constructed. Corresponding to the different multicomplex units in these extensions, real, hyperbolic or imaginary, the wave equations and their solutions exhibit multiple versions of antilinear or 𝒫𝒯-symmetries. Utilizing these symmetries forces certain components of the conserved quantities to vanish, so that one may enforce them to be real. We find that symmetrizing the noncommutative equations is equivalent to imposing a 𝒫𝒯-symmetry for a newly defined imaginary unit from combinations of imaginary and hyperbolic units in the canonical representation.

Copyright
Β© 2020 The Authors. Published by Atlantis and Taylor & Francis
Open Access
This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).

1. Introduction

The underlying mathematical structure of quantum mechanics, a Hilbert space over the field of complex numbers, can be generalized and modified in various different ways. One may for instance re-define the inner product of the Hilbert space or alter, typically enlarge, the field over which this space is defined. The first approach has been pursued successfully since around twenty years [8], when it was first realized that the modification of the inner product allows to include non-Hermitian Hamiltonians into the framework of a quantum mechanical theory. When these non-Hermitian Hamiltonians are 𝒫𝒯-symmetric/quasi-Hermitian [7, 28, 32] they possess real eigenvalues when their eigenfunctions are also 𝒫𝒯-symmetric or pairs of complex conjugate eigenvalues when the latter is not the case. The reality of the spectrum might only hold in some domain of the coupling constant, but break down at what is usually referred to as an exceptional point when at least two eigenvalues coalesce. Higher order exceptional points may occur for larger degeneracies. In order to unravel the structure of the neighbourhood of these points one can make use of the second possibility of generalizations of standard quantum mechanics and change the type of fields over which the Hilbert space is defined. This view helps to understand the bifurcation structure at these points and has been recently investigated for the analytically continued Gross-Pitaevskii equation with bicomplex interaction terms [16, 18, 21]. In a similar spirit, systems with finite dimensional Hilbert spaces have been formulated over Galois fields [37]. Hyperbolic extensions of the complex Hilbert space have been studied in [38]. The standard SchrΓΆdinger equation was bicomplexified in [3] and further studied in [4–6, 35]. Quaternionic and coquaternionic quantum mechanics and quantum field theory have been studied for a long time, see e.g. [2, 19, 20], mainly motivated by the fact that they may be related to various groups and algebras that play a central role in physics, such as SO(3), the Lorentz group, the Clifford algebra or the conformal group. Recently it was suggested that they [9] provide a unifying framework for complexified classical and quantum mechanics. Octonionic Hilbert spaces have been utilized for instance in the study of quark structures [22].

Drawing on various relations between the quantum mechanical setting and classical integrable nonlinear systems that possess soliton solutions, such as the formal identification of the L operator in a Lax pair as a Hamiltonian, many of the above possibilities can also been explored in the latter context. Most direct are the analogues of the field extensions. Previously we demonstrated [12, 13] that one may consistently extend real classical integrable nonlinear systems to the complex domain by maintaining the reality of the energy. Here we go further and investigate multicomplex versions of these type of nonlinear equations. We demonstrate how these equations can be solved in several multicomplex settings and study some of the properties of the solutions. We explore three different possibilities to construct solutions that are not available in a real setting, i) using multicomplex shifts in a real solutions, ii) exploiting the complex representations by defining a new imaginary unit in terms of multicomplex ones and iii) exploiting the idempotent representation. We take 𝒫𝒯-symmetry as a guiding principle to select out physically meaningful solutions with real conserved quantities, notably real energies. We clarify the roles played by the different types of 𝒫𝒯-symmetries. For the noncommutative versions, that is quaternionic, coquaternionic and octonionic, we find that imposing certain 𝒫𝒯-symmetries corresponds to symmetrizing the noncommutative terms in the nonlinear differential equations.

Our manuscript is organized as follows: In section 2 we discuss the construction of bicomplex multi-solitons for the standard Korteweg de-Vries (KdV) equation and its nonlocal variant. We present two different types of construction schemes leading to solutions with different types of 𝒫𝒯-symmetries. We demonstrate that the conserved quantities constructed from these solutions, in particular the energy, are real. In section 3, 4 and 5 we discuss solution procedures for noncommutative versions of the KdV equation in quaternionic, coquaternionic and octonionic form, respectively. Our conclusions are stated in section 6.

2. Bicomplex solitons

2.1. Bicomplex numbers and functions

We start by briefly recalling some key properties of bicomplex numbers and functions to settle our notations and conventions. Denoting the field of complex numbers with imaginary unit Δ± as

β„‚(ΞΉ)={x+ΞΉy|x,yβˆˆβ„},(2.1)
the bicomplex numbers 𝔹 form an algebra over the complex numbers admitting various equivalent types of representations
𝔹={z1+πš₯z2|z1,z2βˆˆβ„‚(ΞΉ)},(2.2)
={w1+ΞΉw2|w1,w2βˆˆβ„‚(πš₯)},(2.3)
={a1β„“+a2ΞΉ+a3πš₯+a4k|a1,a2,a3,a4βˆˆβ„},(2.4)
={v1e1+v2e2|v1βˆˆβ„‚(ΞΉ),v2βˆˆβ„‚(πš₯)}.(2.5)

The canonical basis is spanned by the units β„“, Δ±, πš₯, k, involving the two imaginary units Δ± and πš₯ with Δ±2 = πš₯2 = βˆ’1, so that the representations in equations (2.2) and (2.3) naturally prompt the notion to view these numbers as a doubling of the complex numbers. The real unit β„“ and the hyperbolic unit k = Δ±πš₯ square to 1, β„“2 = k2 = 1. The multiplication of these units is commutative with further products in the Cayley multiplication table being β„“Δ± = Δ±, β„“ πš₯ = πš₯, β„“k = k, Δ±k = βˆ’πš₯, πš₯k = βˆ’Δ±. The idempotent representation (2.5) is an orthogonal decomposition obtained by using the orthogonal idempotents

e1:=1+k2   and   e2:=1βˆ’k2,(2.6)
with properties e12=e1, e22=e2, e1e2 = 0 and e1 + e2 = 1. All four representations (2.2)–(2.5) are uniquely related to each other. For instance, given a bicomplex number in the canonical representation (2.4) in the form
na=a1β„“+a2ΞΉ+a3πš₯+a4k,(2.7)
the equivalent representations (2.2), (2.4) and (2.5) are obtained with the identifications
z1=a1+ΞΉa2,z2=a3+ΞΉa4,w1=a1+πš₯a3,w2=a2+πš₯a4,v1a=(a1+a4)β„“+(a2βˆ’a3)ΞΉ,v2a=(a1βˆ’a4)β„“+(a2+a3)πš₯.(2.8)

Arithmetic operations are most elegantly and efficiently carried out in the idempotent representation (2.5). For the composition of two arbitrary numbers na and nb we have

na∘nb=v1a∘v1be1+v2a∘v2be2   withβ€‰β€‰β€‰βˆ˜β‰‘Β±,β‹…,Γ·.(2.9)

The hyperbolic numbers (or split-complex numbers) 𝔻 = {a1β„“ + a4k | a1, a4 ∈ ℝ} are an important special case of 𝔹 obtained in the absence of the imaginary units Δ± and πš₯, or when taking a2 = a3 = 0.

The same arithmetic rules as in (2.9) then apply to bicomplex functions. In what follows we are most interested in functions depending on two real variables x and t of the form f(x, t) = β„“p(x, t) + Δ±q(x, t) + πš₯r(x, t) + ks(x, t) ∈ 𝔹 involving four real fields p(x, t), q(x, t), r(x, t), s(x, t) ∈ ℝ. Having kept the functional variables real, we also keep our differential real, so that we can differentiate f (x, t) componentwise as βˆ‚x f(x, t) = β„“βˆ‚x p(x, t) + Δ±βˆ‚xq(x, t) + πš₯βˆ‚xr(x, t) + kβˆ‚xs(x, t) and similarly for βˆ‚t f(x, t). For further properties of bicomplex numbers and functions, such as for instance computing norms, see for instance [17, 26, 29, 30].

2.2. 𝒫𝒯-symmetric bicomplex functions and conserved quantities

As there are two different imaginary units, there are three different types of conjugations for bicomplex numbers, corresponding to conjugating only Δ±, only πš₯ or conjugating both Δ± and πš₯ simultaneously. This is reflected in different symmetries that leave the Cayley multiplication table invariant. As a consequence we also have three different types of bicomplex 𝒫𝒯-symmetries, acting as

𝒫𝒯ιπš₯:β„“β†’β„“,ΞΉβ†’βˆ’ΞΉ,πš₯β†’βˆ’πš₯,kβ†’k,xβ†’βˆ’x,tβ†’βˆ’t,(2.10)
𝒫𝒯ιk:β„“β†’β„“,ΞΉβ†’βˆ’ΞΉ,πš₯β†’πš₯,kβ†’βˆ’k,xβ†’βˆ’x,tβ†’βˆ’t,(2.11)
𝒫𝒯πš₯k:β„“β†’β„“,ΞΉβ†’ΞΉ,πš₯β†’βˆ’πš₯,kβ†’βˆ’k,xβ†’βˆ’x,tβ†’βˆ’t,(2.12)
see also [3]. When decomposing the bicomplex energy eigenvalue of a bicomplex Hamiltonian H in the time-independent SchrΓΆdinger equation, Hψ= Eψ, as E = E1β„“ + E2Δ± + E3 πš₯ + E4k, Bagchi and Banerjee argued in [3] that a 𝒫𝒯ık-symmetry ensures that E2 = E4 = 0, a 𝒫𝒯πš₯k-symmetry forces E3 = E4 = 0 and a 𝒫𝒯ıπš₯-symmetry sets E2 = E3 = 0. In [12–14] we argued that for complex soliton solutions the 𝒫𝒯-symmetries together with the integrability of the model guarantees the reality of all physical conserved quantities. One of the main concerns in this section is to investigate the roles played by the symmetries (2.10)–(2.12) for the bicomplex soliton solutions and to clarify whether the implications are similar as observed in the quantum case.

Decomposing a density function for any conserved quantity as

ρ(x,t)=ℓρ1(x,t)+ιρ2(x,t)+πš₯ρ3(x,t)+kρ4(x,t)βˆˆπ”Ή,(2.13)
and demanding it to be 𝒫𝒯-invariant, it is easily verified that a 𝒫𝒯ık-symmetry implies that ρ1, ρ3 and ρ2, ρ4 are even and odd functions of x, respectively. A 𝒫𝒯 πš₯k-symmetry forces ρ1, ρ2 and ρ3, ρ4 to even and odd in x, respectively and a 𝒫𝒯ıπš₯-symmetry makes ρ1, ρ4 and ρ2, ρ3 even and odd in x, respectively. The corresponding conserved quantities must therefore be of the form
Q=βˆ«βˆ’βˆžβˆžΟ(x,t)dx={Q1β„“+Q3πš₯for  𝒫𝒯ιkβˆ’symmetricρQ1β„“+Q2ΞΉfor   𝒫𝒯πš₯kβˆ’symmetricρQ1β„“+Q4kfor   𝒫𝒯ιπš₯βˆ’symmetricρ,(2.14)
where we denote Qi:=βˆ«βˆ’βˆžβˆžΟi(x,t)dx with i = 1, 2, 3, 4. Thus we expect the same property that forces certain quantum mechanical energies to vanish to hold similarly for all classical conserved quantities. We only regard Q1 and Q4 as physical, so that only a 𝒫𝒯ıπš₯-symmetric system is guaranteed to be physical.

2.3. The bicomplex Korteweg-de Vries equation

Using the multiplication law (2.9) for bicomplex functions, the KdV equation for a bicomplex field in the canonical form

u(x,t)=β„“p(x,t)+ΞΉq(x,t)+πš₯r(x,t)+ks(x,t)βˆˆπ”Ή,(2.15)
can either be viewed as a set of coupled equations for the four real fields p(x, t), q(x, t), r(x, t), s(x, t) ∈ ℝ
ut+6uux+uxxx=0⇔{pt+6ppxβˆ’6qqxβˆ’6rrx+6ssx+pxxx=0qt+6qpx+6pqxβˆ’6srxβˆ’6rsx+qxxx=0rt+6rpx+6prxβˆ’6qsxβˆ’6sqx+rxxx=0st+6spx+6psx+6qrx+6rqx+sxxx=0,(2.16)
or when using the representation (2.5) as a couple of complex KdV equations
vt+6vvx+vxxx=0,   and   wt+6wwx+wxxx=0,(2.17)
related to the canonical representation as
v(x,t)=[p(x,t)+s(x,t)]+ΞΉ[q(x,t)βˆ’r(x,t)]βˆˆβ„‚(ΞΉ), (2.18)
w(x,t)=[p(x,t)βˆ’s(x,t)]+πš₯[q(x,t)+r(x,t)]βˆˆβ„‚(πš₯),(2.19)

We recall that we keep here our space and time variables, x and t, to be both real so that also the corresponding derivatives βˆ‚x and βˆ‚t are not bicomplexified.

When acting on the component functions the 𝒫𝒯-symmetries (2.10)–(2.12) are implemented in (2.16) as

𝒫𝒯ιπš₯:xβ†’βˆ’x,tβ†’βˆ’t,pβ†’p,qβ†’βˆ’q,rβ†’βˆ’r,sβ†’s,uβ†’u,(2.20)
𝒫𝒯ιk:xβ†’βˆ’x,tβ†’βˆ’t,pβ†’p,qβ†’βˆ’q,rβ†’r,sβ†’βˆ’s,uβ†’u,(2.21)
𝒫𝒯πš₯k:xβ†’βˆ’x,tβ†’βˆ’t,pβ†’p,qβ†’q,rβ†’βˆ’r,sβ†’βˆ’s,uβ†’u,(2.22)
ensuring that the KdV-equation remains invariant for all of the transformations. Notice that the representation in (2.17) remains only invariant under 𝒫𝒯ıπš₯, but does not respect the symmetries 𝒫𝒯ık and 𝒫𝒯πš₯k.

We observe that (2.16) allows for a scaling of space by the hyperbolic unit k as x β†’ k x, leading to a new type of KdV-equation with u β†’ h

kht+6hhx+hxxx=0⇔{st+6ppxβˆ’6qqxβˆ’6rrx+6ssx+pxxx=0rtβˆ’6qpxβˆ’6pqx+6srx+6rsxβˆ’qxxx=0qtβˆ’6rpxβˆ’6prxβˆ’6qsx+6sqxβˆ’rxxx=0pt+6spx+6psx+6qrx+6rqx+sxxx=0,(2.23)
that also respects the 𝒫𝒯ıπš₯-symmetry. The interesting consequence of this modification is that traveling wave solutions u(ΞΎ) of (2.16) depending on real combination of x and t as ΞΎ = x + ct ∈ ℝ, with c denoting the speed, become solutions h(ΞΆ) dependent on the hyperbolic number ΞΆ = kx +ct ∈ 𝔻 instead. Interestingly a hyperbolic rotation of this number ΞΆ, defined as ΞΆβ€² = ΞΆeβˆ’Ο•k = kxβ€² + ctβ€² with Ο• = arctan(v/c), constitutes a Lorentz transformation with tβ€² = Ξ³(t βˆ’ v/c2x), xβ€² = Ξ³(t βˆ’ vx) and Ξ³=11βˆ’v2/c2, see e.g. [34, 36].

Next we consider various solutions to these different versions of the bicomplex KdV-equation, discuss how they may be constructed and their key properties.

2.3.1. One-soliton solutions with broken 𝒫𝒯-symmetry

We start from the well known bright one-soliton solution of the real KdV equation (2.16)

uΞΌ,Ξ±(x,t)=Ξ±22sech2[12(Ξ±xβˆ’Ξ±3t+ΞΌ)],(2.24)
when Ξ±, μ∈ ℝ. Since our differentials have not been bicomplexified we may take ΞΌ to be a bicomplex number ΞΌ = ρℓ + ΞΈΔ± + Ο•πš₯ + Ο‡k∈ 𝔹 with ρ, ΞΈ, Ο•, Ο‡ ∈ ℝ, so that (2.24) becomes a solution of the bicomplex equation (2.16). We may of course also take to be bicomplex, but as we commented in [13] already on the complex case, this would imply losing the 𝒫𝒯-symmetry and would also lead to non real, hence unphysical, conserved quantities. Expanding the hyperbolic function, we can separate the bicomplex function uΞΌ,Ξ±(x, t) after some lengthy computation into its different canonical components
uρ,ΞΈ,Ο•,Ο‡;Ξ±=β„“2[pρ+Ο‡,ΞΈβˆ’Ο•;Ξ±+pΟβˆ’Ο‡,ΞΈ+Ο•;Ξ±]+ΞΉ2[qρ+Ο‡,ΞΈβˆ’Ο•;Ξ±+qΟβˆ’Ο‡,ΞΈ+Ο•;Ξ±]   +πš₯2[qΟβˆ’Ο‡,ΞΈ+Ο•;Ξ±βˆ’qρ+Ο‡,ΞΈβˆ’Ο•;Ξ±]+k2[pρ+Ο‡,ΞΈβˆ’Ο•;Ξ±βˆ’pΟβˆ’Ο‡,ΞΈ+Ο•;Ξ±],(2.25)
when using the two functions
pa,b;Ξ±(x,t)=Ξ±2+Ξ±2cosbcosh(Ξ±xβˆ’Ξ±3t+a)[cosb+cosh(Ξ±xβˆ’Ξ±3t+a)]2,(2.26)
qa,b;Ξ±(x,t)=Ξ±2sinbsinh(Ξ±xβˆ’Ξ±3t+a)[cosb+cosh(Ξ±xβˆ’Ξ±3t+a)]2.(2.27)

Noting that the complex solution uiΞΈ,Ξ±(x, t) studied in [13], can be expressed as uiΞΈ,Ξ±(x, t) = pa,ΞΈ;Ξ±(x βˆ’ a/Ξ±, t)+iqa,ΞΈ;Ξ±(x βˆ’ a/Ξ±, t), we can also expand the bicomplex solution (2.25) in terms of the complex solution as

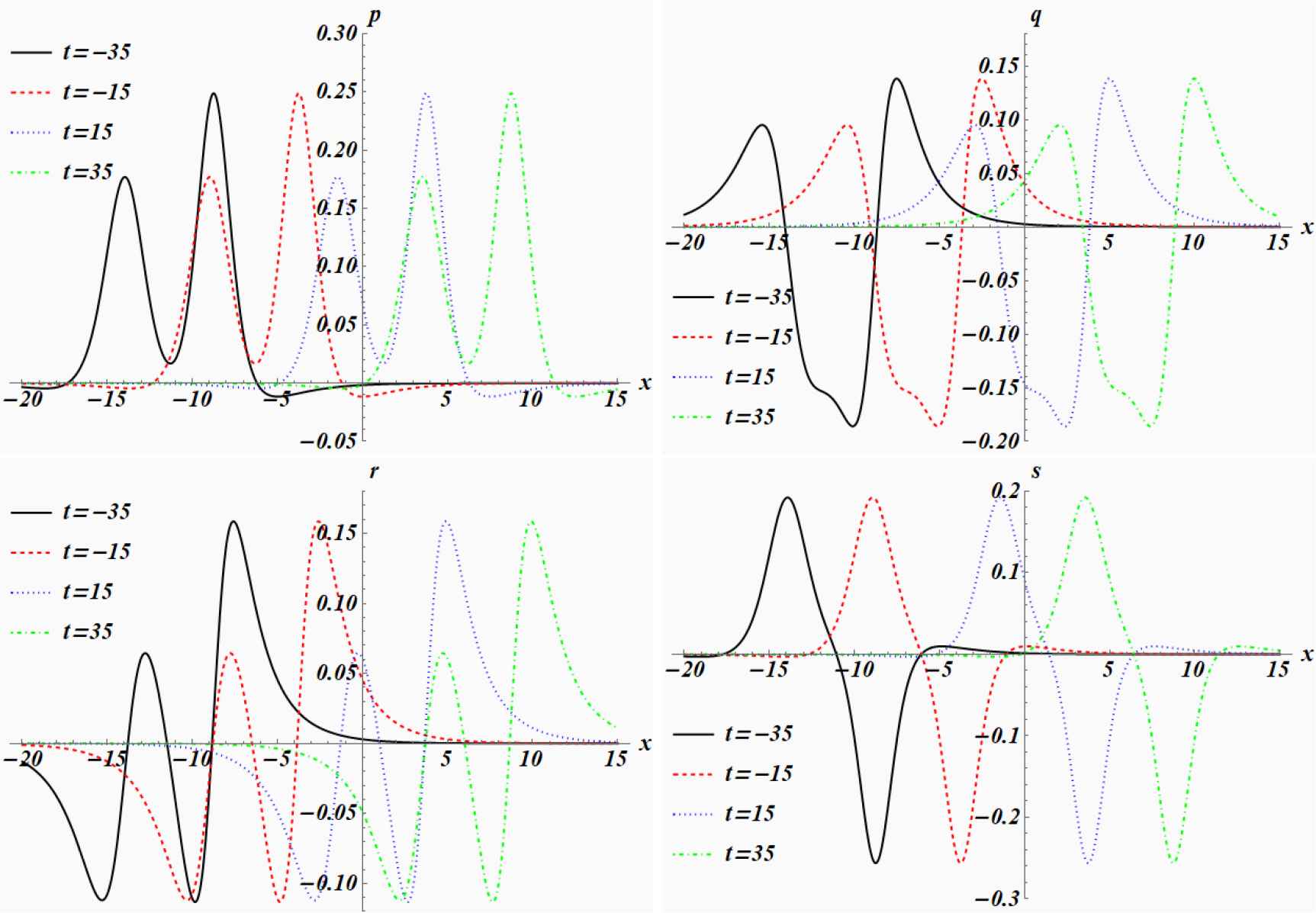
uρ,ΞΈ,Ο•,Ο‡;Ξ±=β„“2[ui(Ο•βˆ’ΞΈ),Ξ±(x+ρ+χα,t)+uβˆ’i(Ο•+ΞΈ),Ξ±(x+Οβˆ’Ο‡Ξ±,t)]   +k2[uβˆ’i(Ο•βˆ’ΞΈ),Ξ±(x+ρ+χα,t)βˆ’ui(Ο•+ΞΈ),Ξ±(x+Οβˆ’Ο‡Ξ±,t)].(2.28)

Fig. 1.

Canonical component functions p, q, r and s (clockwise starting in the top left corner) of the decomposed onesoliton solution uρ,ΞΈ,Ο•,Ο‡;Ξ± to the bicomplex KdV equation (2.16) with broken 𝒫𝒯-symmetry at different times for Ξ± = 0.5, ρ = 1.3, ΞΈ = 0.4, Ο• = 2.0 and Ο‡ = 1.3.

In figure 2.3.1 we depict the canonical components of this solution at different times. We observe in all of them that the one-soliton solution is split into two separate one-soliton-like components moving parallel to each other with the same speed. The real p-component can be viewed as the sum of two bright solitons and the hyperbolic s-component is the sum of a bright and a dark soliton. This effect is the results of the decomposition of each of the components into a sum of the functions pa,b;Ξ± or qa,b;Ξ±, as defined in (2.26), at different values of a, b, but the same value of Ξ±. Since a and b control the amplitude and distance, whereas regulates the speed, the constituents travel at the same speed. We recall that this type of behaviour of degenerate solitons can neither be created from a real nor a complex two-soliton solution [11, 15]. So this is a novel type of phenomenon for solitons previously not observed.

Fig. 2.

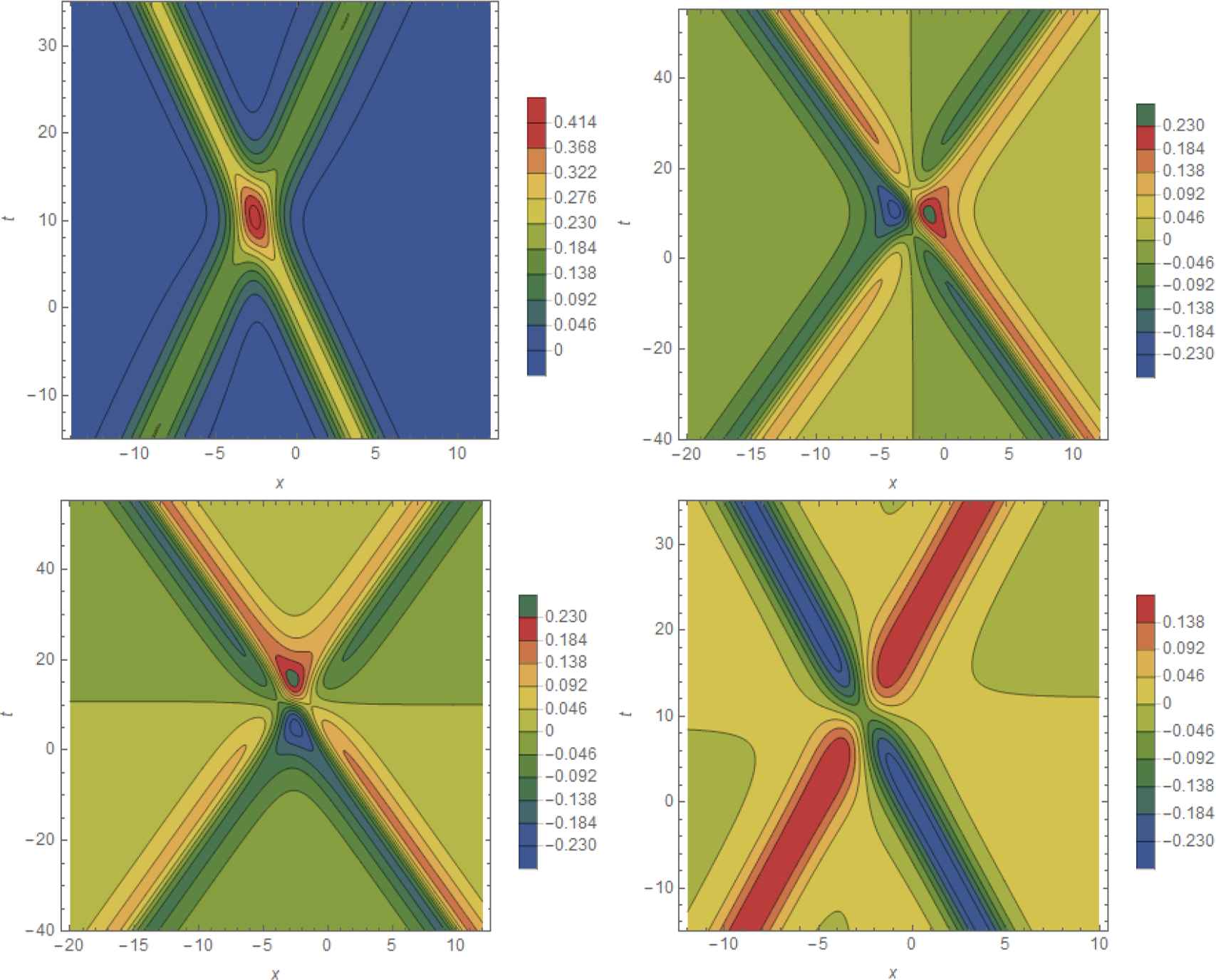
Head-on collision of a bright soliton with a dark soliton in the canonical components p, q, r, s (clockwise starting in the top left corner) for the one-soliton solution hρ,ΞΈ,Ο•,Ο‡;Ξ± to the bicomplex KdV equation (2.16) with broken 𝒫𝒯-symmetry for Ξ± = 0.5, ρ = 1.3, ΞΈ = 0.1, Ο• = 2.0 and Ο‡ = 1.3. Time is running vertically, space horizontally and contours of the amplitudes are colour-coded indicated as in the legends.

In general, the solution (2.24) is not 𝒫𝒯-symmetric with regard to any of the possibilities defined above. It becomes 𝒫𝒯ıπš₯-symmetric when ρ = Ο‡ = 0, 𝒫𝒯ık-symmetric when ρ = Ο‡ = Ο• = 0 and 𝒫𝒯jk-symmetric when ρ = Ο‡ = ΞΈ = 0.

A solution to the new KdV equation (2.23) is constructed as

hΞΌ,Ξ±(x,t)=Ξ±22sech2[12(Ξ±xkβˆ’Ξ±3t+ΞΌ)],(2.29)
which in component form reads
hρ,ΞΈ,Ο•,Ο‡;Ξ±=β„“2[pΒ―Ο‡βˆ’Ο,ΞΈ+Ο•;Ξ±+pΟ‡+ρ,ΞΈβˆ’Ο•;Ξ±]+ΞΉ2[qΒ―Ο‡βˆ’Ο,ΞΈ+Ο•;Ξ±βˆ’qΟ‡+ρ,ΞΈβˆ’Ο•;Ξ±]   +k2[qΒ―Ο‡βˆ’Ο,ΞΈ+Ο•;Ξ±+qΟ‡+ρ,ΞΈβˆ’Ο•;Ξ±]+k2[pΒ―Ο‡+ρ,ΞΈβˆ’Ο•;Ξ±βˆ’pΟ‡βˆ’Ο,ΞΈ+Ο•;Ξ±],(2.30)
where we introduced the notation pΒ―a,b;Ξ±(x,t)=pa,b;Ξ±(x,βˆ’t) and qΒ―a,b;Ξ±(x,t)=qa,b;Ξ±(x,βˆ’t).

In figure 2.3.1 we depict the canonical component functions of this solution. We observe that the one-soliton solution is split into two one-soliton-like structures that scatter head-on with each other. The real p-component consists of a head-on scattering of two bright solitons and hyperbolic the s-component is a head-on collision of a bright and a dark soliton. Given that uρ,ΞΈ,Ο•,Ο‡;Ξ± and hρ,ΞΈ,Ο•,Ο‡;Ξ±(x, t) differ in the way that one of its constituent functions is time-reversed this is to be expected.

2.3.2. 𝒫𝒯ij-symmetric one-soliton solution

An interesting solution can be constructed when we start with a complex 𝒫𝒯ık and a complex 𝒫𝒯πš₯k symmetric solution to assemble the linear decomposition of an overall 𝒫𝒯ıπš₯-symmetric solution with different velocities. Taking in the decomposition (2.17) v(x, t) = uΔ±ΞΈ,Ξ±(x, t) and w(x, t) = uπš₯Ο•,Ξ²(x, t), we can build the bicomplex KdV-solution in the idempotent representation

u^ΞΈ,Ο•;Ξ±,Ξ²(x,t)=uΞΉΞΈ,Ξ±(x,t)e1+uπš₯Ο•,Ξ²(x,t)e2.(2.31)

The expanded version in the canonical representation becomes in this case

u^ΞΈ,Ο•;Ξ±,Ξ²=β„“2[p0,ΞΈ;Ξ±+p0,Ο•;Ξ²]+ΞΉ2[q0,ΞΈ;Ξ±+q0,Ο•;Ξ²]+πš₯2[q0,Ο•;Ξ²βˆ’q0,ΞΈ;Ξ±]+k2[p0,ΞΈ;Ξ±βˆ’p0,Ο•;Ξ²],(2.32)
which is evidently 𝒫𝒯ıπš₯-symmetric. Hence this solution contain any multicomplex shifts, but in each component two solitonic contributions with different amplitude and speed parameter. As we can see in figure 2.3.2, in the real p-component a faster bright soliton is overtaking a slower bright solitons and in hyperbolic s-component a faster bright soliton is overtaking and a slower dark soliton. Unlike as in the real or complex case, one can carry out the limit Ξ² β†’ Ξ± to the degenerate case without complication since have the identity ûθ,βˆ’Ο•,ΞΈ+Ο•;Ξ±,Ξ± = u0,ΞΈ,Ο•,0;Ξ±. Similarly as in the previous section we may also construct a further solution from a hyperbolic shift x β†’ kx, which we do not present here.

Fig. 3.

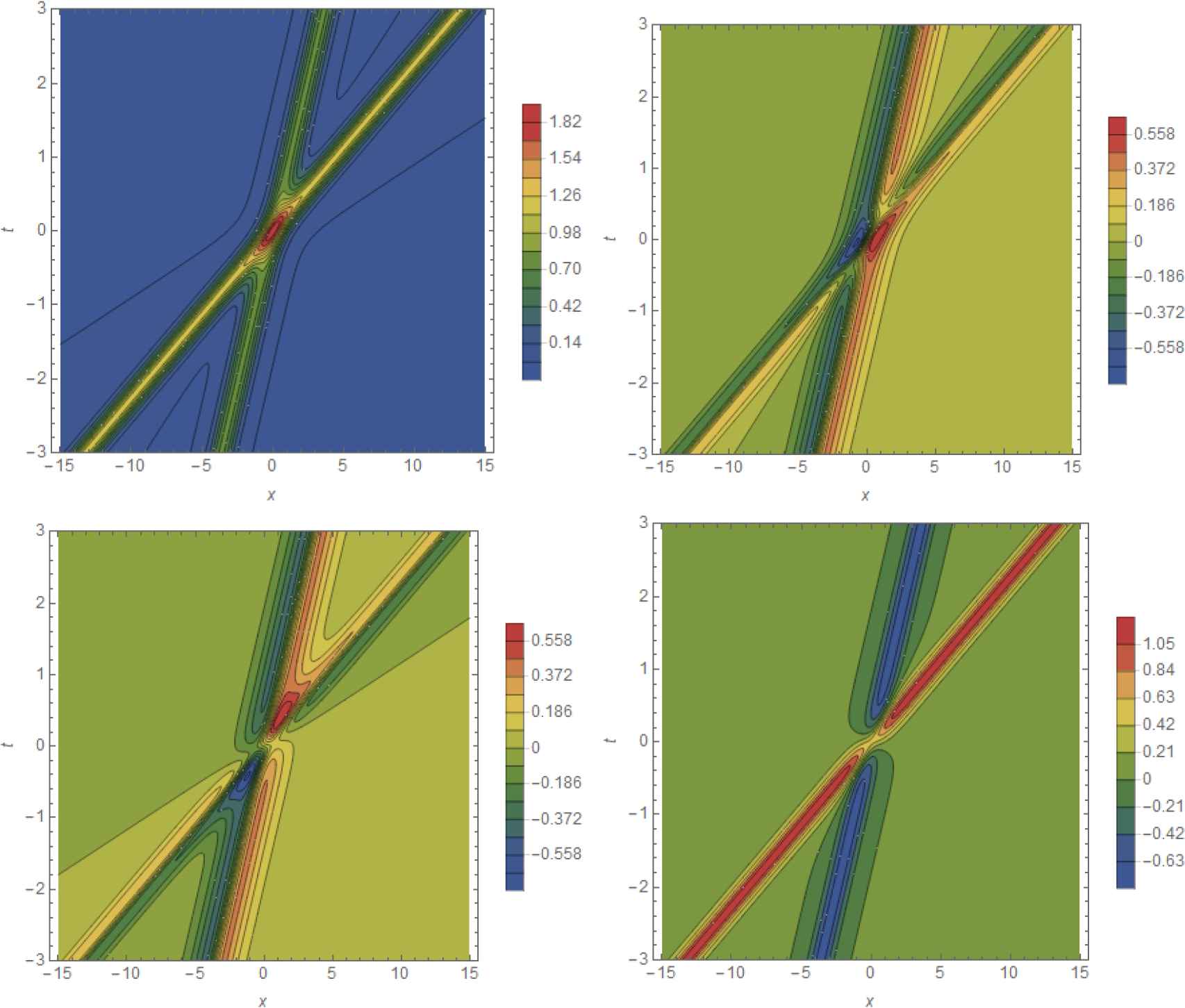
A fast bright soliton overtaking a slower bright soliton in the canonical component functions p, q, r and s (clockwise starting in the top left corner) for the one-soliton solution ûθ,Ο•;Ξ±,Ξ² to the bicomplex KdV equation (2.16) with 𝒫𝒯ij-symmetry for Ξ± = 2.1, Ξ² = 1.1, ΞΈ = 0.6 and Ο• = 1.75.

2.3.3. Multi-soliton solutions

The most compact way to express the N-soliton solution for the real KdV equation in the form (2.16) is

uΞΌ1,ΞΌ2,…,ΞΌn;Ξ±1,Ξ±2,…,Ξ±n(n)(x,t)=2[lnWn(ψμ1,Ξ±1,ψμ2,Ξ±2,…,ψμn,Ξ±n)]xx,(2.33)
where Wn[ψ1, ψ 2, . . ., ψn] := detΟ‰ denotes the Wronskian with Ο‰jk = βˆ‚jβˆ’1ψk/βˆ‚xjβˆ’1 for j, k = 1, . . ., n, e.g. W1[ψ0] = ψ0, W2[ψ0, ψ1] = ψ0 (ψ1)x βˆ’ ψ1 (ψ0)x, etc and the functions ψi are solutions to the time-independent SchrΓΆdinger equation for the free theory. Taking for instance ψμ,Ξ±(x, t) = cosh[(Ξ±x βˆ’ Ξ±3t + ΞΌ)/2] for n = 1 leads to the one-soliton solution (2.24).

We could now take the shifts ΞΌ1, ΞΌ2, . . ., ΞΌn ∈ 𝔹 and expand (2.33) into its canonical components to obtain the N-soliton solution for the bicomplex equation. Alternatively we may also construct N-solitons in the idempotent basis in analogy to (2.32). We demonstrate here the latter approach for the two-soliton. From (2.33) we observe that the second derivative will not alter the linear bicomplex decomposition and it is therefore useful to introduce the quantity w(x, t) as u = wx. Thus a complex one-soliton solution can be obtained from

wa,b;Ξ±(x,t)=wa,b;Ξ±r(x,t)+ΞΉwa,b;Ξ±i(x,t)(2.34)
with
wa,b;Ξ±r(x,t)=Ξ±sinh(Ξ±xβˆ’Ξ±3t+a)cosb+cosh(Ξ±xβˆ’Ξ±3t+a),   wa,b;Ξ±i(x,t)=Ξ±sinbcosb+cosh(Ξ±xβˆ’Ξ±3t+a).(2.35)

Noting that pa,b;Ξ±=(wa,b;Ξ±r)x, qa,b;Ξ±=(wa,b;Ξ±i)x we obtain a complex soliton as ua,b;Ξ± = (wa,b;Ξ±)x. Recalling now the expression

wa,b,c,d;Ξ±,Ξ²=Ξ±2βˆ’Ξ²2wa,b;Ξ±βˆ’wc,d;Ξ²,(2.36)
from the BΓ€cklund transformation of the complex two-soliton [13], we can express this in terms of the functions in (2.35)
wa,b,c,d;Ξ±,Ξ²=(Ξ±2βˆ’Ξ²2)[(wa,b;Ξ±rβˆ’wc,d;Ξ²r)βˆ’ΞΉ(wa,b;Ξ±iβˆ’wc,d;Ξ²i)](wa,b;Ξ±rβˆ’wc,d;Ξ²r)2+(wa,b;Ξ±iβˆ’wc,d;Ξ²i)=wa,b,c,d;Ξ±,Ξ²r+ΞΉwa,b,c,d;Ξ±,Ξ²i.(2.37)

Using (2.37) to define the two complex quantities wΞΈ1,ΞΈ2,ΞΈ3,ΞΈ4;Ξ±1,Ξ±2=w2r+ΞΉw2iβˆˆβ„‚(ΞΉ) and wΟ•1,Ο•2,Ο•3,Ο•4;Ξ²1,Ξ²2=w˜2r+πš₯w˜2iβˆˆβ„‚(πš₯) we introduce the bicomplex function

w2=(w2r+ΞΉw2i)e1+(w˜2r+πš₯w˜2i)e2(2.38)
=β„“2(w2r+w˜2r)+ΞΉ2(w2i+w˜2i)+πš₯2(w˜2iβˆ’w2i)+k2(w2rβˆ’w˜2r).(2.39)

Then by construction uΞΈ1,ΞΈ2,ΞΈ3,ΞΈ4,Ο•1,Ο•2,Ο•3,Ο•4;Ξ±1,Ξ±2,Ξ²1,Ξ²2 = (w2)x is a bicomplex two-soliton solution with four speed parameters. In a similar fashion we can proceed to construct N-soliton for N > 2.

2.3.4. Real and hyperbolic conserved quantities

Next we compute the first conserved quantities the mass m, the momentum p and the energy E, see e.g. [12, 13]

m(u)=βˆ«βˆ’βˆžβˆžudx=m1β„“+m2ΞΉ+m3πš₯+m4k,(2.40)
p(u)=βˆ«βˆ’βˆžβˆžu2dx=p1β„“+p2ΞΉ+p3πš₯+p4k,(2.41)
E(u)=βˆ«βˆ’βˆžβˆž(12ux2βˆ’u3)dx=E1β„“+E2ΞΉ+E3πš₯+E4k(2.42)

Decomposing the relevant densities into the canonical basis, u as in (2.15), u2 as

u2=(p2βˆ’q2βˆ’r2+s2)β„“+2(pqβˆ’rs)ΞΉ+2(prβˆ’qs)πš₯+2(qr+ps)k(2.43)
and the Hamiltonian density β„‹(u,ux)=ux2/2βˆ’u3 as
β„‹=[3p(q2+r2βˆ’s2)+px2βˆ’qx2βˆ’rx2+sx22βˆ’6qrsβˆ’p3]ℓ   +[q3βˆ’3p2q+pxqx+6prs+3q(r2βˆ’s2)βˆ’rxsx]ι   +[r3+6pqs+3r(q2βˆ’s2βˆ’p2)+pxrxβˆ’qxsx]πš₯   +[3s(r2βˆ’p2+q2]βˆ’6pqr+pxsx+qxrxβˆ’s3]k,(2.44)
we integrate componentwise. For the solutions uρ,ΞΈ,Ο•,Ο‡;Ξ± and hρ,ΞΈ,Ο•,Ο‡;Ξ± with broken 𝒫𝒯-symmetry we obtain the real conserved quantities
m(uρ,ΞΈ,Ο•,Ο‡;Ξ±)=m(hρ,ΞΈ,Ο•,Ο‡;Ξ±)=2Ξ±β„“,(2.45)
p(uρ,ΞΈ,Ο•,Ο‡;Ξ±)=p(hρ,ΞΈ,Ο•,Ο‡;Ξ±)=23Ξ±3β„“, (2.46)
E(uρ,ΞΈ,Ο•,Ο‡;Ξ±)=E(hρ,ΞΈ,Ο•,Ο‡;Ξ±)=βˆ’15Ξ±5β„“.(2.47)

These values are the same as those found in [13] for the complex solitons. Given that the 𝒫𝒯-symmetries are all broken this is surprising at first sight. However, considering the representation (2.28) this is easily understood when using the result of [13]. Then m(uρ,ΞΈ,Ο•,Ο‡;Ξ±) is simply β„“/2(2Ξ± + 2Ξ±) + πš₯/2(2Ξ± βˆ’ 2Ξ±) = 2Ξ±β„“. We can argue similarly for the other conserved quantities.

For the 𝒫𝒯ij-symmetric solution ûθ,Ο•;Ξ±,Ξ² we obtain the following hyperbolic values for the conserved quantities

m(u^ΞΈ,Ο•;Ξ±,Ξ²)=(Ξ±+Ξ²)β„“+(Ξ±βˆ’Ξ²)k,(2.48)
p(u^ΞΈ,Ο•;Ξ±,Ξ²)=13(Ξ±3+Ξ²3)β„“+13(Ξ±3βˆ’Ξ²3)k(2.49)
E(u^ΞΈ,Ο•;Ξ±,Ξ²)=βˆ’(Ξ±510+Ξ²510)β„“+(Ξ²510βˆ’Ξ±510)k.(2.50)

The values become real and coincide with the expressions (2.45)–(2.47) when we sum up the contributions from the real and hyperbolic component or in the degenerate case when we take the limit Ξ² β†’ Ξ±.

2.4. The bicomplex Alice and Bob KdV equation

Various nonlocal versions of nonlinear wave equations that have been overlooked previously have attracted considerable attention recently. In reference to standard scenarios in quantum cryptography some of them are also often referred to as Alice and Bob systems. These variants of the nonlinear SchrΓΆdinger or Hirota equation [1, 10, 27, 33] arise from an alternative choice in the compatibility condition of the two AKNS-equations. For the KdV equation (2.16) they can be constructed [23–25] by choosing u(x, t) = 1/2[a(x, t) + b(x, t)], with the constraint 𝒫𝒯 a(x, t) = a(βˆ’x, βˆ’t) = b(x, t), thus converting it into an equation that can be decomposed into two equations, the Alice and Bob KdV (ABKdV) equation

at+3/4(a+b)(3ax+bx)+axxx=0.(2.51)
bt+3/4(a+b)(ax+3bx)+bxxx=0.(2.52)

In a similar way as the two AKNS-equations can be made compatible by a suitable transformation map, these two equations are converted into each other by a 𝒫𝒯-transformation, i.e. 𝒫𝒯 (2.51) ≑ (2.52). Evidently the decomposition is not unique and one may also add and subtract a constrained function of a and b or consider different types of maps to relate the equation.

The bicomplex version of the Alice and Bob system (2.51), (2.52) is obtained by taking a, b ∈ 𝔹. In the canonical basis we use the conventions u(x, t) = β„“p(x, t) + Δ±q(x, t) + πš₯r(x, t) + ks(x, t), a(x,t)=β„“p^(x,t)+ΞΉq^(x,t)+πš₯r^(x,t)+ks^(x,t), b(x,t)=β„“p̌(x,t)+ΞΉq̌(x,t)+πš₯ř(x,t)+kš(x,t), so that the ABKdV equations (2.51) and (2.52) decompose into eight coupled equations

p^t=βˆ’p^xxxβˆ’32[p(p̌x+3p^x)βˆ’q(q̌x+3q^x)βˆ’r(řx+3r^x)+s(šx+3s^x)],(2.53)
q^t=βˆ’q^xxx+32[p(q̌x+3q^x)+q(p̌x+3p^x)βˆ’r(šx+3s^x)βˆ’s(řx+3r^x)],(2.54)
r^t=βˆ’r^xxx+32[p(řx+3r^x)βˆ’q(šx+3s^x)+r(p̌x+3p^x)βˆ’s(q̌x+3q^x)],(2.55)
s^t=βˆ’s^xxx+32[p(šx+3s^x)+q(řx+3r^x)+r(q̌x+3q^x)+s(p̌x+3p^x)],(2.56)
and
p̌t=βˆ’p̌xxx+32[p(3p̌x+3p^x)βˆ’q(3q̌x+q^x)βˆ’r(3řx+r^x)+s(3šx+s^x)],(2.57)
q̌t=βˆ’q̌xxx+32[p(3q̌x+q^x)+q(3p̌x+p^x)βˆ’r(3šx+s^x)βˆ’s(3řx+r^x)],(2.58)
řt=βˆ’řxxx+32[p(3řx+r^x)βˆ’q(3šx+s^x)+r(3p̌x+p^x)βˆ’s(3q̌x+q^x)],(2.59)
št=βˆ’šxxx+32[p(3šx+s^x)+q(3řx+r^x)+r(3q̌x+q^x)+s(3p̌x+p^x)].(2.60)

A real solution to the ABKdV equations (2.51) and (2.52) that sums up to the standard one-soliton solution (2.24) is found asx

aΞΌ,Ξ½;Ξ±(x,t)=uΞΌ,Ξ±(x,t)+Ξ½tanh[12(Ξ±xβˆ’Ξ±3t+ΞΌ)],(2.61)
bΞΌ,Ξ½;Ξ±(x,t)=uΞΌ,Ξ±(x,t)βˆ’Ξ½tanh[12(Ξ±xβˆ’Ξ±3t+ΞΌ)],(2.62)
with arbitrary constants Ξ½, ΞΌ ∈ ℝ. Proceeding now as for the local variant by taking ΞΌ = ρℓ + Δ± + Ο•πš₯ + Ο‡k ∈ 𝔹, we decompose aΞΌ,Ξ½;Ξ± and bΞΌ,Ξ½;Ξ± into their canonical components and obtain after some lengthy computation the corresponding solution to the bicomplex version of the ABKdV equations (2.53)–(2.60) as
aρ,ΞΈ,Ο•,Ο‡;Ξ±=uρ,ΞΈ,Ο•,Ο‡;Ξ±+β„“2Ξ½Fw+ρ,ΞΈ,Ο•,Ο‡+ΞΉ2Ξ½Gw+ρ,ΞΈ,Ο•,Ο‡+πš₯2Ξ½Gw+ρ,Ο•,ΞΈ,Ο‡+k2Ξ½FΟ‡,ΞΈ,Ο•,q+ρ(2.63)
with wΞ± = Ξ±x βˆ’ Ξ±3t and the newly defined functions
Fx1,x2,x3,x4=sinhx1secx2secx3sechx4+tanhx1βˆ’tanx2tanx3tanhx41βˆ’tanhx1tanx2tanx3tanhx4+cosh(2x1)+cos(2x2)+cos(2x3)+cosh(2x4)4coshx1cosx2cosx3coshx4,(2.64)
Gx1,x2,x3,x4=sechx1secx2sinx3sechx4+tanx3+tanhx1tanx2tanhx41βˆ’tanhx1tanx2tanx3tanhx4+cosh(2x1)+cos(2x2)+cos(2x3)+cosh(2x4)4coshx1cosx2cosx3coshx4.(2.65)

The functions bρ,ΞΈ,Ο•,Ο‡;Ξ±, or equivalently the individual components p̌, q̌, ř, š, are obtained by a 𝒫𝒯-transformation.

We may also proceed as in subsection 2.3.2 and construct a solution in the idempotent representation. Keeping the parameter real, a solution based on the idempotent decomposition is

aΞΈ,Ο•,Ξ½;Ξ±,Ξ²=aiΞΈ,Ξ½;Ξ±e1+aiΟ•,Ξ½;Ξ²e2   =u^ΞΈ,Ο•;Ξ±,Ξ²+β„“2Ξ½(FwΞ±,ΞΈ,0,0+FwΞ²,Ο•,0,0)+ΞΉ2Ξ½(GwΞ±,0,ΞΈ,0+GwΞ²,0,Ο•,0)   +πš₯2Ξ½(GwΞ²,0,Ο•,0+GwΞ±,0,ΞΈ,0)+k2Ξ½(FwΞ±,ΞΈ,0,0βˆ’GwΞ²,Ο•,0,0).(2.66)

Once more, the functions bρ,ΞΈ,Ο•,Ο‡;Ξ± or p̌, q̌, ř, š are obtained by a 𝒫𝒯-transformation. Comparing (2.66) with aρ,ΞΈ,Ο•,Ο‡;Ξ± in (2.63) we have now two speed parameters at our disposal, similarly as in the local case.

3. Quaternionic solitons

3.1. Quaternionic numbers and functions

The quaternions in the canonical basis are defined as the set of elements

𝕇={a1β„“+a2ΞΉ+a3πš₯+a4k|a1,a2,a3,a4βˆˆβ„}.(3.1)

The multiplication of the basis {β„“,Δ±, πš₯, k} is noncommutative with β„“ denoting the real unit element, β„“2 = 1 and Δ±, πš₯, k its three imaginary units with Δ±2 = πš₯2 = k2 = βˆ’1. The remaining multiplication rules are Δ±πš₯ = βˆ’ πš₯Δ± = k, πš₯k = βˆ’kπš₯ = Δ± and kΔ± = βˆ’Δ±k = πš₯. The multiplication table remains invariant under the symmetries 𝒫𝒯ıπš₯, 𝒫𝒯ık and 𝒫𝒯πš₯k. Using these rules for the basis, two quaternions in the canonical basis na = a1β„“ + a2Δ± + a3 πš₯ + a4k ∈ 𝕇 and nb = b1β„“ + b2Δ± + b3πš₯ + b4k ∈ 𝕇 are multiplied as

nanb=(a1b1βˆ’a2b2βˆ’a3b3βˆ’a4b4)β„“+(a1b2+a2b1+a3b4βˆ’a4b3)ι   +(a1b3βˆ’a2b4+a3b1+a4b2)πš₯+(a1b4+a2b3βˆ’a3b2+a4b1)k.(3.2)

There are various representations for quaternions, see e.g. [31], of which the complex form will be especially useful for what follows. With the help of (3.2) one easily verifies that

ΞΎ:=1𝒩(a2ΞΉ+a3πš₯+a4k)   with   𝒩=a22+a32+a42(3.3)
constitutes a new imaginary unit with ΞΎ2 = βˆ’1. This means that in this representation we can formally view a quaternion, na ∈ 𝕇, as an element in the complex numbers
na=a1β„“+ΞΎπ’©βˆˆβ„‚(ΞΎ),(3.4)
with real part a1 and imaginary part 𝒩. Notice that a 𝒫𝒯ξ-symmetry can only be achieved with a 𝒫𝒯ıπš₯k-symmetry acting on the unit vectors in the canonical representation. Unlike the bicomplex numbers or the coquaternions, see below, the quaternionic algebra does not contain any idempotents.

3.2. The quaternionic Korteweg-de Vries equation

Applying now the multiplication law (3.2) to quaternionic functions, the KdV equation for a quaternionic field of the form u(x, t) = β„“p(x, t) + Δ±q(x, t) + πš₯r(x, t) + ks(x, t) ∈ 𝕇 can also be viewed as a set of coupled equations for the four real fields p(x, t), q(x, t), r(x, t), s(x, t) ∈ ℝ

ut+6uux+uxxx=0⇔{pt+6ppxβˆ’6qqxβˆ’6rrx+6ssx+pxxx=0qt+6qpx+6pqxβˆ’6srx+6rsx+qxxx=0rt+6rpx+6prxβˆ’6qsxβˆ’6sqx+rxxx=0st+6spx+6psx+6qrxβˆ’6rqx+sxxx=0.(3.5)

Notice that when comparing the bicomplex KdV equation (2.16) and the quaternionic KdV equation (3.5) only the signs of the penultimate terms in all four equations have changed. This means that also (3.5) is invariant under the 𝒫𝒯ıπš₯-symmetry. Alternatively, we may consider here the aforementioned symmetry

𝒫𝒯ιπš₯k:xβ†’βˆ’x,tβ†’βˆ’t,ΞΉβ†’βˆ’ΞΉ,πš₯β†’βˆ’πš₯,kβ†’βˆ’k,pβ†’βˆ’p,qβ†’βˆ’q,rβ†’βˆ’r,sβ†’βˆ’s,uβ†’u,(3.6)
which violates all the noncommutative multiplication rules Δ±πš₯ = βˆ’πš₯Δ± = k, πš₯k = βˆ’kπš₯ = Δ± and kΔ± = βˆ’Δ±k = πš₯. Thus in order to implement the symmetry 𝒫𝒯ıπš₯k we must set all terms resulting from these multiplications to zero, so that we obtain the additional constraints
srx=rsx,   qsx=sqx,   and   qrx=rqx.(3.7)

When eliminating these terms from (3.5) the remaining set of equations is 𝒫𝒯ıπš₯k-symmetric, which appears to be a rather strong imposition. However, the equations without these terms emerge quite naturally when keeping in mind that the product of functions in (3.5) is noncommutative so that one should symmetrize products and replace 6uux β†’ 3uux + 3uxu. This process corresponds precisely to imposing the constraints (3.7).

3.3. 𝒫𝒯ıπš₯k-symmetric N-soliton solutions

Due to the noncommutative nature of the quaternions it appears difficult at first sight to find solutions to the quaternionic KdV equation. However, using the complex representation (3.4), and imposing the 𝒫𝒯ıπš₯k-symmetric, we may resort to our previous analysis on complex solitons. Following [13] and considering the shifted solution (2.24) in the complex space β„‚(ΞΎ) yields the solution

ua1β„“+ξ𝒩,Ξ±(x,t)=pa1,𝒩;Ξ±(x,t)βˆ’ΞΎqa1,𝒩;Ξ±(x,t)(3.8)
=pa1,𝒩;Ξ±(x,t)β„“βˆ’1𝒩qa1,𝒩;Ξ±(x,t)(a2ΞΉ+a3πš₯+a4k).(3.9)

This solution becomes 𝒫𝒯ıπš₯k-symmetric when we carry out a shift in x or t to eliminate the real part of the shift. Reading off the functions p(x, t), q(x, t), r(x, t), s(x, t) from (3.9), it is also obvious that the constraints (3.7) are indeed satisfied. Thus the real β„“-component is a one-solitonic structure similar to the real part of a complex soliton and the remaining component consists of the imaginary parts of a complex soliton with overall different amplitudes. It is clear that the conserved quantities constructed from this solution must be real, which follows by using the same argument as for the imaginary part in the complex case [13] separately for each of the Δ±, πš₯, k-components. By considering all functions to be in β„‚(ΞΎ), it is also clear that multi-soliton solutions can be constructed in analogy to the complex case β„‚(Δ±) treated in [13] with a subsequent expansion into canonical components.

Since the quaternionic algebra does not contain any idempotents, a construction similar to the one carried out in subsection 2.3.2 does not seem to be possible for quaternions. However, we can use (2.36) for two complex solutions wa,b;Ξ±(x,t)=wa,b;Ξ±r(x,t)+ΞΎΞ±wa,b;Ξ±i(x,t), wc,d;Ξ²(x,t)=wc,d;Ξ²r(x,t)+ΞΎbwc,d;Ξ²i(x,t), where the imaginary units are defined as in (3.3) with ΞΎa(a2, a3, a4) and ΞΎb(b2, b3, b4). Expanding that expression in the canonical basis we obtain

w2=Ξ±2βˆ’Ξ²2Ο‰12+Ο‰22+Ο‰32+Ο‰42(β„“Ο‰1βˆ’ΞΉΟ‰2βˆ’πš₯Ο‰3βˆ’kΟ‰4) (3.10)
with
Ο‰1=wa,b;Ξ±rβˆ’wc,d;Ξ²r,   ωn=anwa,b;Ξ±i𝒩aβˆ’bnwc,d;Ξ²i𝒩b,   n=2,3,4.(3.11)

A coquaternionic two-soliton solution to (3.5) is then obtained from (3.10) as u(2) = (w2)x.

4. Coquaternionic solitons

4.1. Coquaternionic numbers and functions

The coquaternions or often also referred to as split-quaternions in the canonical basis are defined as the set of elements

𝕇={a1β„“+a2ΞΉ+a3πš₯+a4k|a1,a2,a3,a4βˆˆβ„}.(4.1)

The multiplication of the basis {β„“,Δ±, πš₯, k} is noncommutative with a real unit element β„“, β„“2 = 1, two hyperbolic unit elements πš₯, k, πš₯2 = k2 = 1, and one imaginary unit Δ±2 = βˆ’1. The remaining multiplication rules are Δ±πš₯ = βˆ’πš₯Δ± = k, πš₯k = βˆ’k πš₯= βˆ’Δ± and kΔ± = βˆ’Δ±k = πš₯. The multiplication table remains invariant under the symmetries 𝒫𝒯ıπš₯, 𝒫𝒯ık and 𝒫𝒯πš₯k. Using these rules for the basis, two coquaternions in the canonical basis na = a1β„“ + a2Δ±+ a3πš₯ + a4k ∈ 𝕇 and nb = b1β„“ + b2Δ±+ b3πš₯ + b4k ∈ 𝕇 are multiplied as

nanb=(a1b1βˆ’a2b2βˆ’a3b3βˆ’a4b4)β„“+(a1b2+a2b1βˆ’a3b4+a4b3)ι   +(a1b3βˆ’a2b4+a3b1+a4b2)πš₯+k(a1b4+a2b3βˆ’a3b2+a4b1)k.(4.2)

There are various coquaternionic representations for numbers and functions. Similar as a quaternion one can formally view a coquaternion, n1 ∈ 𝕇, as an element in the complex numbers

na=a1β„“+ΞΆβ„³βˆˆβ„‚(ΞΆ)(4.3)
with real part a1 and imaginary part β„³. The new imaginary unit, ΞΆ2 = βˆ’1,
ΞΆ:=1β„³(a2ΞΉ+a3πš₯+a4k)   with   ℳ=a22βˆ’a32βˆ’a42(4.4)
is, however, only defined for a22β‰ a32+a42. For definiteness we assume here |a2|>a32+a42. Similarly as the 𝒫𝒯ξ-symmerty also the 𝒫𝒯΢-symmerty requires a 𝒫𝒯ıπš₯k-symmetry. Unlike the quaternions, the coquaternions possess a number idempotents e1 = (1 + k)/2, e2 = (1 βˆ’ k)/2 with e12=e1, e22=e2, e1e2 = 0 or e3 = (1 + πš₯)/2, e4 = (1 βˆ’ πš₯)/2 with e32=e3, e42=e4, e3e4 = 0. So for instance, na is an element in
𝕇={e1v1+e2v2|v1βˆˆπ”»(πš₯),  v2βˆˆπ”»(πš₯)},(4.5)
where the hyperbolic numbers in (4.5) are related to the coefficient in the canonical basis as v1 = (a1 + a4)β„“ + (a2 + a3)πš₯ and v2 = (a1 βˆ’ a4)β„“ + (a3 βˆ’ a2)πš₯.

4.2. The coquaternionic Korteweg-de Vries equation

Applying now the multiplication law (4.2) to coquaternionic functions, the KdV equation for a quaternionic field of the form u(x, t) = β„“p(x, t) + Δ±q(x, t) + πš₯r(x, t) + ks(x, t) ∈ 𝕇 can also be viewed as a set of coupled equations for the four real fields p(x, t), q(x, t), r(x, t), s(x, t) ∈ ℝ. The symmetric coquaternionic KdV equation then becomes

ut+3(uux+uxu)+uxxx=0⇔{pt+6ppxβˆ’6qqxβˆ’6ssx+6rrx+pxxx=0qt+6qpx+6pqx+qxxx=0rt+6rpx+6prx+rxxx=0st+6spx+6psx+sxxx=0.(4.6)

Notice that the last three equations of the coupled equation in (4.6) are identical to the symmetric quaternionic KdV equation (3.5) with constraints (3.7).

4.3. 𝒫𝒯ıπš₯k-symmetric N-soliton solutions

Using the representation (4.3) we proceed as in subsection 3.3 and consider the shifted solution (2.24) in the complex space β„‚(ΞΆ)

ua1β„“+ΞΆβ„³,Ξ±(x,t)=pa1,β„³;Ξ±(x,t)βˆ’ΞΆqa1,β„³;Ξ±(x,t)(4.7)
=pa1,β„³;Ξ±(x,t)β„“βˆ’1β„³qa1,β„³;Ξ±(x,t)(a2ΞΉ+a3πš₯+a4k)(4.8)
that solves the coquaternionic KdV equation (4.6). The solution in (4.7) is 𝒫𝒯ıπš₯k-symmetric. Multi-soliton solutions can be constructed in analogy to the complex case β„‚(Δ±) treated in [13] by treating all functions in β„‚(ΞΆ) as explained in more detail at the end of section 4.

5. Octonionic solitons

We finish our discussion with a comment on the construction of octonionic solitons. Octonions or Cayley numbers are extensions of the quaternions with a doubling of the dimensions. In the canonical basis they can be represented as

𝕆={a0e0+a1e1+a2e2+a3e3+a4e4+a5e5+a6e6+a7e7|aiβˆˆβ„}.(5.1)

The multiplication of the units is defined by noting that each of the seven quadruplets (e0, e1, e2, e3), (e0, e1, e4, e5), (e0, e1, e7, e6), (e0, e2, e4, e6), (e0, e2, e5, e7), (e0, e3, e4, e7) and (e0, e3, e6, e5), constitutes a canonical basis for the quaternions in one-to-one correspondence with (β„“,Δ±,πš₯,k). Hence the octonions have one real unit, 7 imaginary units and the multiplication of two octonions is noncommutative. Similarly as for quaternions and coquaternions we can view an octonion na ∈ 𝕆 as a complex number

na=a1β„“+oπ’ͺβˆˆβ„‚(o)(5.2)
with real part a1, imaginary part π’ͺ and newly defined imaginary unit, o2 = βˆ’1,
o:=1π’ͺβˆ‘i=17a1e1   where  π’ͺ=βˆ‘i=17a1e1.(5.3)

In order to obtain a 𝒫𝒯o-symmetry we require a 𝒫𝒯e1e2e3e4e5e6e7-symmetry in the canonical basis.

5.1. The octonionic Korteweg-de Vries equation

Taking now an octonionic field to be of the form u(x, t) = p(x, t)e0 + q(x, t)e1 + r(x, t)e2 + s(x, t)e3 + t(x, t)e4 + v(x, t)e5 + w(x, t)e6 + z(x, t)e7 ∈ 𝕆 the symmetric octonionic KdV equation, in this form of (4.6) becomes a set of eight coupled equations

p4+6ppxβˆ’6qqxβˆ’6rrxβˆ’6ssxβˆ’6ttxβˆ’6vvxβˆ’6wwxβˆ’6zzx+pxxx=0,Ο‡t+6Ο‡px+6pΟ‡x+Ο‡xxx=0,(5.4)
with Ο‡ = q, r, s, t, v, w, z. Setting any of four variables for Ο‡ to zero reduces (5.4) to the coupled set of equations corresponding to the symmetric quaternionic KdV equation (3.5) with constraints (3.7).

5.2. 𝒫𝒯e1e2e3e4e5e6e7-symmetric N-soliton solutions

Using the representation (5.2) we proceed as in subsection 3.3 and consider the shifted solution (2.24) in the complex space β„‚(o)

ua1β„“+oπ’ͺ,Ξ±(x,t)=pa1,π’ͺ;Ξ±(x,t)βˆ’oqa1,π’ͺ;Ξ±(x,t)(5.5)
=pa1,π’ͺ;Ξ±(x,t)β„“βˆ’1π’ͺqa1,π’ͺ;Ξ±(x,t)βˆ‘i=17a1e1(5.6)
that solves the octonionic KdV equation (5.4). The solution in (5.5) is 𝒫𝒯e1e2e3e4e5e6e7-symmetric. Once more, multi-soliton solutions can be constructed in analogy to the complex case β„‚(Δ±) treated in [13] by treating all functions in β„‚(o) as explained in more detail at the end of section 4.

6. Conclusions

We have shown that the bicomplex, quaternionic, coquaternionic and octonionic versions of the KdV equation admit multi-soliton solutions. Using the standard folklore we assume that the existence of such type of solutions implies certain integrability of these equations, which we did not formally prove. The bicomplex versions, local and nonlocal, display a particularly rich structure with the two types of solutions found to exhibit very different types of qualitative behaviour. Especially interesting is the solution in the idempotent representation that decomposes a N-soliton into a 2N-solitonic structure. Each one-soliton constituent of the N-soliton has two contributions that even involve two independent speed parameters. Unlike as for the real and complex solitons, where the degeneracy poses a nontrivial technical problem [11, 15], here these parameters can be trivially set to be equal.

For all noncommuative versions of the KdV equation, i.e. quaternionic, coquaternionic and octonionic, we found multi-soliton solutions based on complex representation in which the imaginary unit is built from specific combinations of the imaginary and hyperbolic units. Interestingly in all cases we observe that the 𝒫𝒯-symmetry needed to ensure that the newly defined imaginary unit can also be used as a 𝒫𝒯-symmetry imposes constraints that are equivalent to the constraints needed to obtain the symmetric KdV equation from the nonsymmetric one.

Naturally it would be interesting to extend the analysis presented here to other types of nonlinear integrable systems. A more challenging extension is to multi-complexify also the variables x and t which then also impacts on the definition of the derivatives with respect to these variables.

Acknowledgments

JC is supported by a City, University of London Research Fellowship.

References

[2]S.L. Adler, Quaternionic quantum mechanics and quantum fields, Oxford University Press on Demand, Vol. 88, 1995.
[23]S.Y. Lou, 2016. Alice-Bob systems, Ps-Td-C principles and multi-soliton solutions, arXiv preprint arXiv:1603.03975
[29]G.B. Price, An introduction to multicomplex spaces and functions, M. Dekker inc, New York, 1991.
[30]D. Rochon and M. Shapiro, On algebraic properties of bicomplex and hyperbolic numbers, Anal. Univ. Oradea, Fasc. Math., Vol. 11, No. 28, 2004, pp. 110.
<Previous Article In Issue
Download article (PDF)
Next Article In Issue>
Journal
Journal of Nonlinear Mathematical Physics
Volume-Issue
27 - 1
Pages
17 - 35
Publication Date
2019/10/25
ISSN (Online)
1776-0852
ISSN (Print)
1402-9251
DOI
10.1080/14029251.2020.1683963How to use a DOI?
Copyright
Β© 2020 The Authors. Published by Atlantis and Taylor & Francis
Open Access
This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).

Cite this article

risenwbib
TY  - JOUR
AU  - Julia Cen
AU  - Andreas Fring
PY  - 2019
DA  - 2019/10/25
TI  - Multicomplex solitons
JO  - Journal of Nonlinear Mathematical Physics
SP  - 17
EP  - 35
VL  - 27
IS  - 1
SN  - 1776-0852
UR  - https://doi.org/10.1080/14029251.2020.1683963
DO  - 10.1080/14029251.2020.1683963
ID  - Cen2019
ER  -