A case retrieval method combined with similarity measurement and DEA model for alternative generation
- DOI
- 10.2991/ijcis.11.1.85How to use a DOI?
- Keywords
- Case-based reasoning; DEA model; multiple criteria decision analysis; prospect theory; similarity measurement
- Abstract
In alternative generation, reusing past experience is a potential methodology and case retrieval is a primary step. In order to improve the performance of case retrieval process, many applications have used different similarity measurements and the selection method for the most suitable historical case to solve problems. Many investigations have shown that human beings are usually bounded rational and their psychological behavior has certain influence on decision making. However, such behavior is neglected in similarity measurements and the selection method can only deal with the evaluation given by one decision maker (DM). This paper proposes a new case retrieval method that combines similarity measurement and data envelopment analysis (DEA) model. A similarity measurement based on cumulative prospect theory is proposed to consider the DM’s psychological behavior. A hybridization of four similarity measurements is used to generate a set of similar historical cases. The DM evaluates the similar historical case set by a pairwise comparison matrix. A DEA model is constructed to get the priority vector. The most suitable historical case can then be picked out through the case similarity and the case priority. A case study is finally introduced to illustrate the use of the proposed method.
- Copyright
- © 2018, the Authors. Published by Atlantis Press.
- Open Access
- This is an open access article under the CC BY-NC license (http://creativecommons.org/licences/by-nc/4.0/).
1. Introduction
Case-based reasoning (CBR) is good at solving new problems by referring to the solution of similar past experience1. It can help decision maker (DM) to generate alternatives quickly. Therefore, it has been widely used in many fields, such as environment preparedness system2, emergency decision making3, business failure prediction4, medicine5, fault diagnosis6, wastewater treatment7. CBR usually includes four steps1, i.e., retrieval, adaptation, revision and retaining. Among the four steps, retrieval is regarded as the first and core step. If the retrieved historical case(s) is the most desirable case, the solution will be effective; otherwise, the result would not be good. Hence, it is essential to study case retrieval methods.
Up to now, a number of case retrieval methods have been proposed in the practical CBR applications. There are mainly two kinds. One kind is to propose a similarity function to retrieve the similar historical case(s) and directly use it in the applications. For example, Kwong et al.8 proposed a similarity measure based on Euclidean distance to concurrent design of low power transformers. Yu et al.9 developed a hybridization of both symbolic and numeric reasoning techniques for mining of scarce construction databases. Li et al.4 proposed a similarity computation method, which transferred the attribute distance into Gaussian distance and solved the nonlinear data, to improve the prediction accuracy in business failure prediction. Sun et al.10 developed a similarity function using grey theory to improve the ability of similar case retrieval and prediction accuracy. Li et al.11 proposed a similarity measure by combining four independent CBR models to amplify advantages of individual techniques and minimize their limitations. Apparently, it is useful to mix several similarity measure methods. The other kind of methods proposed case similarity measurements and selected the appropriate historical case(s) according to the evaluation of historical cases. To select the most desirable historical case, some studies attempted to introduce multi-criteria decision making (MCDM) to select the most effective historical case. For example, Qi et al.12 proposed a case retrieval method which used the algorithm of order preference by similarity to an ideal solution (TOPSIS) to evaluate the most similar cases in terms of product criteria to pick out the most suitable case. Li et al.13 developed a CBR forecasting method based on the similarities to positive and negative ideal cases. Fan et al.3 generated the desirable response alternative by evaluating the retrieved historical case(s).
The existing studies have made significant contributions to decision making based on CBR. These studies provided various retrieval methods for DMs to solve problems. However, among the existing studies, the similarity calculation methods have a premise, that is, the DM is perfectly rational. In fact, the DM has some emotions such as rejoicing regret, or dislike, in decision making14, and they would affect the DM's decision. In other words, people are often limitedly rational rather than perfectly rational when facing decision making. Therefore, it is necessary to investigate the case retrieval methods considering human behavior for the purpose of providing effective decision support to DMs. Furthermore, the existing case selection methods can only deal with the evaluation given by one DM, yet the process of decision making may have several formats such as in group decision-making. Therefore, case retrieval methods should consider the psychological behavior in the similarity calculation and several evaluation formats in the most suitable historical case selection.
Since Tversky and Kaheneman proposed cumulative prospect theory (CPT)15, which is a descriptive model of decision making under conditions of risk, many scholars have employed it to solve various decision-making problems considering DM’s behavior, such as, emergency decision making16, MCDM17. This is because CPT describes the DM’s behavior characteristics well and gives the calculation formulas on values and weights of potential outcome. In the case retrieval step, the DM usually has some emotions, i.e., loss aversion, diminishing sensitivity, and reference dependence. For instance, the DM has a thought that if the attribute value of one historical case is very different from the target case, even the case similarity is higher than the other historical cases, the historical case is not similar with the target case. Therefore, how to incorporate CPT into case retrieval deserves more attention.
Extensive studies of MCDM techniques have been undertaken over the past decades, where methods of analytic hierarchy process (AHP), elimination and choice translating reality (ELECTRE), and technique for TOPSIS have been proved to be effective approaches. TOPSIS method has been integrated into CBR to generate a more suitable alternative. But TOPSIS has a defect that cannot handle large set of alternatives and criteria18. AHP is a simple and effective MCDM aid tool, and it can evaluate several similar cases and identify a suitable design alternative. Rammanathan19 developed a method which combined data envelopment analysis (DEA) with AHP to form a DEAHP method, but it has a significant drawback that there is no guarantee that the DEAHP method can produce rational weight vectors for inconsistent pairwise comparison matrices (PCM). Afterwards, Wang et al.20 proposed a new DEA model to determine the priority, which can derive logical priorities for PCM. Hence, how to derive the priority vector in the AHP for the similar case set is worth attention.
The objective of this paper is to develop a case retrieval method based on similarity measurement and DEA model for generating a desirable alternative. In similarity measurement stage, a similarity measurement based on CPT is proposed, which considers DM’s psychological behavioral. It is more consistent with decision-making process. Meanwhile, we mix three classic similarity methods with the similarity measurement based on CPT to get proper similar historical cases set. The mix can expand the advantages of the similarity measurements and make the decision result more effective. In alternative generation stage, a DEA model is constructed to get the priority vector in AHP, and generate a proper alternative. The DEA model can deal with various forms of evaluations and make the method more applicable.
The rest of the paper is organized as follows. In section 2, we give a brief review of the classic similarity measurements and CPT. In section 3, we develop a case retrieval method combined with similarity measurement and DEA model for alternative generation. In section 4, numerical examples are provided to illustrate the use of the proposed method. In section 5, the discussion of this study is presented. In section 6, conclusions of this study are provided.
2. Preliminaries
This section provides a brief introduction about concepts related to similarity measurement and CPT that are used in the later proposed method.
2.1. Similarity measurement
Case retrieval is the core step of the CBR. Similarity measurement between target case and historical cases has great influence on retrieval quality. The similarity assessment based on distance function is the typical measurement, such as, Euclidean distance11, Manhattan distance11, Gaussian distance4. We assume the attribute distance between historical case Cg and target case C0 concerning the attribute Pl is d0gl, l ∈ {1, 2, …, m}, g ∈ {1, 2, …, h} and the formula for the case similarity based on Euclidean distance
We assume the attribute distance between historical case Cg and target case C0 concerning the attribute Pl is g0gl, and the formula for the case similarity based on Gausian distance
Then, in order to improve the performance of retrieval, grey coefficient degree11 is used to calculate the similarity. Assume the attribute distance between historical case Cg and target case C0 concerning the attribute Pl is rogl, and the formula for the case similarity based on grey coefficient
The CBR model built on grey coefficient degree is called RCBR.
2.2 CPT method
A lot of psychological studies have shown that there are several psychological characteristics of human behavior under risk and uncertainty, such as reference dependence, loss aversion, and judgmental distortion of likelihood of almost impossible and certain outcomes16, 21, 22. The decision-making problem is uncertain and risk sometimes, so it is necessary to consider DMs’ psychological behavior. Since Tversky and Kaheneman proposed CPT, many scholars have employed it to solve various decision-making problems considering DM’s behavior, such as, emergency decision making16, MCMD17. CPT includes two steps. Firstly, the outcomes of gains and losses are calculated by a reference point and the prospect value is evaluated by a value function. The value function is expressed in the form of a power law according to the following expression22
3. The proposed method
In this section, we present a method for case retrieval which combines similarity measurement and DEA model for alternative generation as Fig. 1. Firstly a hybrid similarity measurement is proposed, which mixes the similarity measurement based on CPT with three classic similarity measurements. Then alternative evaluation is got using PCM. Furthermore, a DEA model is constructed to gain the priority of the similar historical cases. Finally we gain the ranking order of the similar historical case and the desirable historical case will be determined. The method is introduced as follows.
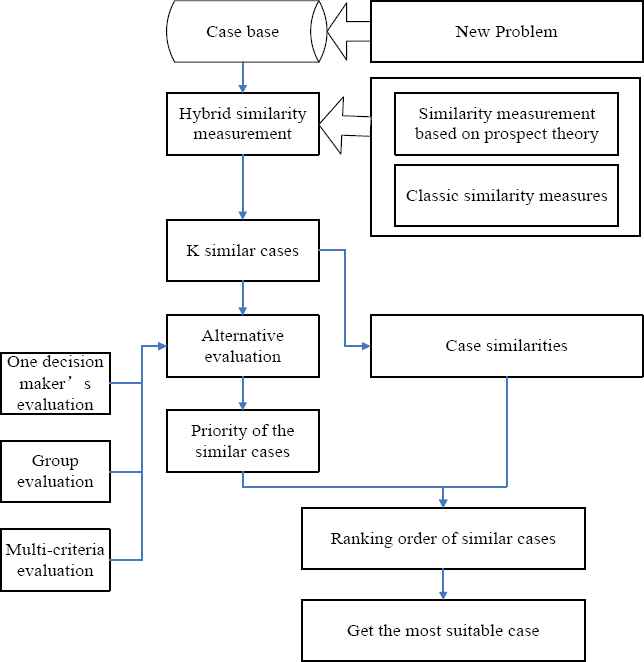
Framework of the case retrieval model
3.1. Similarity measurement
In order to amplify the advantages of similarity measurements and minimize their limitations11, the combination of several similarity measurements is employed to gain the similarities between historical cases and target case. The case similarity measurement includes two aspects and is shown in Fig. 2. The first aspect is to calculate the case similarity based on prospect theory, the other aspect is to calculate the case similarity based on three classic similarity measurements.
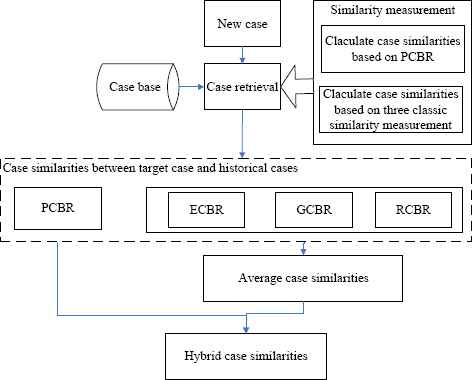
The process of the hybrid similarity calculation
3.1.1. Similarity measurement based on cumulative prospect theory
Suppose there are g historical cases denoted by Cg(g = 1, …, h) and one target case denoted by C0. Let P = {P1, P2, …, Pm} represent the vector of m attributes with regard to the problem of both the historical cases and the target case, where Pl denotes the lth attribute, l ∈ {1, 2, …, m} Let
Let Sim0gl denote the attribute similarity between historical case Cg and target case C0 concerning the attribute Pl and dl denote a reference point with regard to the lth attribute distance. Because the DM’s preference for the attribute distance is dl, it means that if the attribute distance is less than dl, the DM would feel it is “gain”, otherwise, if the attribute distance is more than dl, the DM would feel it is “loss”. Based on CPT, we can define the attribute similarity Sim0gl between historical case Cg and target case C0 concerning the attribute Pl as follows:
Since different attribute similarities are usually incommensurate, Sim0gl needs to be normalized as
Finally, by using the simple additive weighting (SAW) method, the overall prospect of each historical case similarity Sim″g can be calculated as follows:
The CBR model built on prospect theory is called PCBR.
The following example illustrates the feasibility and effectiveness for the similarity measurement based on CPT.
Example 1
A high-rise building fire took place in City F. The emergency decision center considers four attributes mainly, which are fire rating (P1), fire area (P2, unit: m2), casualties (P3, unit: person) and economic losses (P4, unit: ten thousand RMB). Table 1 shows the attribute values with regard to the target case C0 and historical cases Ci (i = 1, 2, 3). The attribute weight vector provided by the emergency management center is W = (0.25, 0.25, 0.25, 0.25), the DM preference attribute distance vector is (0.4, 0.3, 0.3, 0.3).
| P1 | P2 | P3 | P4 | |
|---|---|---|---|---|
| C1 | 1 | 16 | 18 | 7 |
| C2 | 3 | 19 | 20 | 10 |
| C3 | 4 | 25 | 25 | 11 |
| C0 | 2 | 18 | 20 | 8 |
Attribute values with regard to target case and historical cases
According to Eqs. (1) – (2) , the attribute distance d0gl and case similarity Simg are gained, and the results can be found in Table 2.
| d0g1 | d0g2 | d0g3 | d0g4 | Simg | |
|---|---|---|---|---|---|
| C1 | 0.3333 | 0.2222 | 0.2857 | 0.2500 | 0.7272 |
| C2 | 0.3333 | 0.1111 | 0.0000 | 0.5000 | 0.7639 |
| C3 | 0.6667 | 0.7778 | 0.7143 | 0.7500 | 0.3562 |
The computation result of attribute distance and case similarity using Euclidean distance
According to Eqs. (8) – (11) , the attribute similarity sim0gl and case similarity Sim″g are gained, and the results can be found in Table 3.
| sim0g1 | sim0g2 | sim0g3 | sim0g4 | Sim″g | |
|---|---|---|---|---|---|
| C1 | 0.6971 | 0.7996 | 0.7412 | 0.7741 | 0.7530 |
| C2 | 0.6971 | 0.9005 | 1.0000 | −1.1891 | 0.3521 |
| C3 | −0.8189 | −0.5639 | −0.7106 | −0.6285 | −0.6805 |
The computation result of attribute similarity and case similarity using similarity measurement based on CPT
In Table 2, historical case C2 is the most similar case with the target case C0, but the attribute distance d024 is very large. It means that the target case C0 and the historical case C2 have significant differences on attribute P4 and it would lead to different alternatives for the historical case C2 and the target case C0. So, DMs have their preference in the attribute distance. DMs prefer to choose the historical case with a lower similarity and lower attribute distance as the most similar case. The similarity measurement based on CPT can well express this kind of psychological behavior of DMs. The attribute similarity sim024 in the third row and fifth column of Table 3 is very small, because its attribute distance is larger than the DM preference attribute distance 0.3. The most similar case is C1. Therefore, the similarity measurement based on CPT is in accordance with the DMs’ behavior.
3.1.2. Classic similarity measurement
Classic similarity measurements are proved to be useful for the case retrieval, so we consider their effectiveness. We assemble ECBR, GCBR and RCBR to get the classic case similarity. When the ECBR is got using Eqs. (1) – (2) , GCBR is got using Eqs. (3) – (4) , RCBR is got using Eqs. (5) – (6) , we use weighted mean for aggregating three classic similarity measurements. Let Sim′g be the average similarity of the above three classic similarities. The aggregation formula is given by
In order to aggregate the advantages of these similarity measurements, it is necessary to mix the similarities based on the CPT and the average similarity based on three classic similarities measurements. Let Simg denote the hybrid similarity between the historical case Cg and the target case C0. The calculation of Simg is given by
Let ξ be the threshold for the similarity between target case and historical cases, such that ξ ∈ [min{Simg ∣ g ∈ {1, 2, …, h}}, max{Simg ∣ g ∈ {1, 2, …, h}}]. The bigger the value of ξ is, the higher requirement of the case similarity the DM has. The value of ξ usually is given by the DM according to his (her) experience and the realistic data. When Simg ≥ ξ, the historical case Cg would be extracted, and it would constitute the similar historical cases set ZSim, i.e., ZSim = {Ck∣k ∈ MSim}, where MSim = {g ∣ Simg≥ξ, g = 1, 2, …, h} = {1, 2, …, s}. If the similar case set has only one case, the case would be selected as the most suitable case. Otherwise, we would select the most suitable case by a DEA model.
3.2. Multi-criteria decision making
The DEA model proposed by Wang et al.20 can produce true weights for PCM. Here, we use this DEA model to evaluate the similar cases.
3.2.1. DEA model for alternatives priority
Based on the similar case set, the DM evaluates the alternatives by using a PCM denoted as A1 = (aij)s×s, which satisfies aii = 1 and aji = 1/aij for j ≠ i. Let W = (w1, w2, …, ws) be the priority vector of the matrix A1.
We use a DEA model to get the priority vector of the matrix A1 and get the most suitable historical case. According to [20], we view each row of the matrix A1 as a decision making unit (DMU), each column as an output and assume a dummy input value of one for all the DUMs. Each DMU has s outputs and one dummy constant input, based on which the DEA model for relative score can be formulates as
3.2.2. DEA model for alternatives priority concerning group decision making
In decision analysis, group decision making is usually used to assemble several experts’ wisdom. In order to select the most effective alternative, sometimes DMs use group decision making. We consider several DMs to give their preference on the similar case set ZSim by PCM. Let
First, we use SAW method to aggregate several DMs’ preferences, which means that we integrate the k A(k) into a PCM B = (bij)s×s. The formula is given as follows:
Second, we use the following DEA model20 to gain the priority vector:
By solving the above model (16) for each wi (i = 1, …, s), we will get the best priority vector W*.
3.2.3. DEA model for alternative priority concerning multi-criteria evaluation
In decision making, the DM cannot evaluate the alternative directly sometimes, and what she/he can do is to evaluate the alternative from a few criteria. In this situation, a hierarchical structure often exists as shown in Fig. 3. In order to select the most suitable historical case, we can evaluate the similar historical cases set from different criteria. Between the historical case selection level and the p decision criteria level, we can get a priority vector {v1, v2, …, vp} by solving the model (14) and between the p criteria level and s similar historical cases level, we can get p priority vectors {v1j, v2j, …, vsj} (j = 1, …, p) by solving the model (14). Based on the above priority vectors, we use the SAW to aggregate them and get a global priority vector {w1, w2, …, ws} as follows:
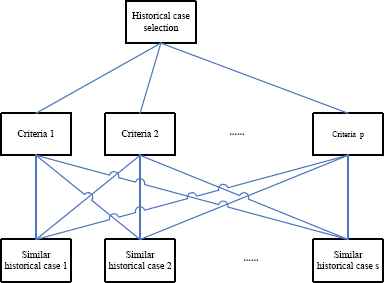
A hierarchical structure for multi-criteria historical case selection
3.3. Comprehensive coefficient
A comprehensive coefficient (CC) is defined to determine the ranking order of the similar historical cases when wi of each similar historical case has been calculated. The case similarity is a very important indicator for selecting the most suitable historical case. So, we should consider the case similarity and the alternative evaluation simultaneously. Let Di denote the CC of the historical case Ci. The calculation formula of Di is given by:
According to Di, we can determine the ranking order of all similar historical cases and select the best cases from the similar historical cases set to generate the alternative of the target case.
In summary, the steps of the proposed method for case retrieval are given as follows:
Step 1. For attribute Pl, calculate the case similarities
Step 2. Calculate the average similarity of the three classic similarities, Sim′g, using Eq. (12) , and the hybrid similarity, Simg, using Eq. (13) .
Step 3. When there is only one DM who gives the evaluation for the similar historical cases, the alternative priority vector W* is determined by model (14); otherwise, by using Eq. (15) and model (16). When the DM evaluates the alternatives from a few criteria, the alternative priority vector W* is determined by model (17).
Step 4. Calculate the comprehensive coefficient Di using Eq. (18) , based on which all the similar historical cases can be ranked and the best historical case(s) can be selected.
4. Example
In this section, we provide a numerical example from three aspects to illustrate the advantages of the proposed method and its potential applications in case retrieval. Consider an application of the proposed method to parametric car design. A car design company E constructs a data base which includes 15 historical cases (C1, C2, …, C15) concerning parametric car design. According to parametric car design, the car design company considers four attributes mainly, namely, hundred kilometers acceleration (P1, unit: second), braking distance (P2, unit: m), horsepower (P3, unit: hp) and hundred kilometers fuel consumption (P4, unit: 1). Now, a new kind of car needs to be designed, and it is regarded as the target case C0. Table 4 shows the values of the attributes with regard to the historical cases Ci and the target case C0. Then we use the case retrieval method combined with similarity measurement and DEA model to generate an alternative. The computation processes and results are presented as follows.
| Cases | P1 | P2 | P3 | P4 |
|---|---|---|---|---|
| C1 | 12 | 42 | 105 | 12 |
| C2 | 11 | 43 | 101 | 12 |
| C3 | 8 | 39 | 110 | 18 |
| C4 | 11 | 41 | 110 | 16 |
| C5 | 10 | 40 | 123 | 17 |
| C6 | 7 | 38 | 128 | 20 |
| C7 | 9 | 43 | 125 | 18 |
| C8 | 6 | 37 | 130 | 20 |
| C9 | 5 | 36 | 130 | 25 |
| C10 | 12 | 45 | 125 | 13 |
| C11 | 10 | 41 | 123 | 14 |
| C12 | 11 | 43 | 121 | 13 |
| C13 | 9 | 40 | 117 | 14 |
| C14 | 7 | 39 | 120 | 17 |
| C15 | 6 | 37 | 117 | 16 |
| C0 | 10 | 42 | 120 | 12 |
The attribute values of the historical cases and the target case
Step 1: The case similarity based on CPT Sim″g can be calculated by using Eqs. (8) – (11) , and the computation results are shown in Table 5.
| Cases | Sim′g | Sim″g | Simg | |||
|---|---|---|---|---|---|---|
| C1 | 0.8328 | 0.7238 | 0.7358 | 0.7642 | 0.2345 | 0.4993 |
| C2 | 0.8148 | 0.6967 | 0.6994 | 0.7370 | 0.3063 | 0.5216 |
| C3 | 0.7373 | 0.5142 | 0.5157 | 0.5890 | 0.2215 | 0.4053 |
| C4 | 0.8152 | 0.6665 | 0.6426 | 0.7081 | 0.2330 | 0.4705 |
| C5 | 0.8492 | 0.7511 | 0.7313 | 0.7772 | 0.3112 | 0.5442 |
| C6 | 0.6939 | 0.4469 | 0.4686 | 0.5365 | −0.4827 | 0.0269 |
| C7 | 0.8183 | 0.6884 | 0.6599 | 0.7222 | 0.3190 | 0.5206 |
| C8 | 0.6571 | 0.3811 | 0.4238 | 0.4873 | −0.3920 | 0.0477 |
| C9 | 0.5947 | 0.3011 | 0.3718 | 0.4225 | −0.1394 | 0.1416 |
| C10 | 0.8216 | 0.6618 | 0.6443 | 0.7093 | 0.5994 | 0.6543 |
| C11 | 0.9157 | 0.8486 | 0.8187 | 0.8610 | 0.6891 | 0.7750 |
| C12 | 0.9163 | 0.8422 | 0.8089 | 0.8558 | 0.6895 | 0.7727 |
| C13 | 0.8654 | 0.7455 | 0.7097 | 0.7735 | 0.6460 | 0.7098 |
| C14 | 0.7772 | 0.6254 | 0.6299 | 0.6775 | –0.1242 | 0.2767 |
| C15 | 0.7223 | 0.5193 | 0.5347 | 0.5921 | –0.4484 | 0.0718 |
The case similarities by five methods
Step 2: The case similarities by using three classic similarity measurements are calculated. The case similaritiy
Step 3: The DMs give the threshold of the case similarity according to his (her) experience, i.e., ξ = 0.5, and we gain the similar cases set, i.e.,
Step 4: The DM gives a PCM A concerning the similar cases set according to his (her) experience as follows:
Step 5: The priority of the similar cases set can be gained by solving model (14), the result is w = (0.0304, 0.0261, 0.0609, 0.0609, 0.5478, 0.1826, 0.0913).
Step 6: Finally, the comprehensive coefficient CC of the similar cases set can be got by using Eq. (18) , the result is Sim = (0.0159, 0.0142, 0.0317, 0.0398, 0.4246, 0.1411, 0.0648). The most suitable historical case is got by ranking CCs and is determined to be C11.
It is indicated from the computational results obtained by using the proposed case retrieval method that the retrieved historical case C11 is the most suitable one to the target case C0. Thus, the design plan for the case C11 can be considered as that for the target case C0. Further, designer of company E can make improvements based on the design plan of C11.
In order to further illustrate the proposed method, alternative selection based on group decision making is described below. Three experts from three different departments are invited to make comparisons about the eight similar historical cases, and the three PCMs provided by them are as follows:
Suppose the relative importance weights of the three DMs are (0.5, 0.3, 0.2), and we use Eq. (15) to transform the three matrices into a matrix B. Then, by solving model (16) for each similar historical case, we get the best priorities shown in the first row of Table 6. If the weights of the three DMs are different, it would get a different matrix B. Then a different priority vector can be derived by model (16). Table 6 shows the best priority vectors derived under different weights of the three DMs. Furthermore, we get the comprehensive coefficient CC of the similar cases set by using Eq. (18) , and the results are shown in Table 7, from which we can see that the most suitable historical case is C11. So we select the alternative of C11 as the finally alternative.
| W1 | W2 | W3 | W4 | W5 | W6 | W7 | |
|---|---|---|---|---|---|---|---|
| (0.5, 0.3, 0.2) | 0.0332 | 0.0468 | 0.0924 | 0.0591 | 0.4188 | 0.2293 | 0.1526 |
| (0.5, 0.25, 0.25) | 0.0329 | 0.0471 | 0.0922 | 0.0590 | 0.4207 | 0.2294 | 0.1529 |
| (0.33, 0.33, 0.33) | 0.0330 | 0.0477 | 0.0894 | 0.0573 | 0.4184 | 0.2302 | 0.1528 |
| (1, 0, 0) | 0.0327 | 0.0445 | 0.0991 | 0.0634 | 0.4223 | 0.2227 | 0.1488 |
| (0,1,0) | 0.0371 | 0.0458 | 0.0880 | 0.0561 | 0.4003 | 0.2362 | 0.1541 |
| (0,0,1) | 0.0300 | 0.0536 | 0.0851 | 0.0549 | 0.4358 | 0.2364 | 0.1587 |
The best priorities of the eight similar historical cases in a group decision making problem
| Sim2 | Sim5 | Sim7 | Sim10 | Sim11 | Sim12 | Sim13 | |
|---|---|---|---|---|---|---|---|
| (0.5, 0.3, 0.2) | 0.0173 | 0.0254 | 0.0481 | 0.0382 | 0.3246 | 0.1772 | 0.1083 |
| (0.5, 0.25, 0.25) | 0.0171 | 0.0256 | 0.0480 | 0.0380 | 0.3260 | 0.1772 | 0.1085 |
| (0.33, 0.33, 0.33) | 0.0172 | 0.0260 | 0.0466 | 0.0371 | 0.3242 | 0.1779 | 0.1085 |
| (1, 0, 0) | 0.0171 | 0.0242 | 0.0516 | 0.0409 | 0.3273 | 0.1721 | 0.1056 |
| (0, 1, 0) | 0.0194 | 0.0249 | 0.0458 | 0.0371 | 0.3102 | 0.1825 | 0.1094 |
| (0, 0, 1) | 0.0157 | 0.0292 | 0.0443 | 0.0341 | 0.3377 | 0.1827 | 0.1126 |
The comprehensive coefficients of the eights similar historical cases
According to the study of [26], we evaluate the alternatives of the similar historical cases from three criteria, such as safety (G1), cost (G2) and accident loss (G3). In order to improve the requirement of similarity, we set the threshold of the similarity as ξ = 0.54, and the similar historical cases set is (C5, C10, C11, C12, C13). Fig 4 shows the hierarchical structure for this alternative selection problem. Table 8 shows the PCM for three criteria. We get the priority weights by solving Eq. (14) , the results are shown in Table 8. Table 9 shows the PCM for the five alternatives with respect to the three criteria. The priority weights are gained by solving Eq. (14) , respectively the results are shown in Table 9. Based on the above results, we get the global priority using Eq.(17) , that is wg = (0.0973, 0.0639, 0.4072, 0.2695, 0.1700). Finally we use Eq. (18) to get the comprehensive coefficient, and the result is that Sim = (0.0530, 0.0418, 0.3156, 0.2083, 0.1207), based on which, we select alternative C11 as the response alternative.

Hierarchy of selection for the most suitable historical case
| G1 | G2 | G3 | Priority | |
|---|---|---|---|---|
| G1 | 1 | 3 | 2 | 0.5294 |
| G2 | 1/3 | 1 | 1/3 | 0.1404 |
| G3 | 1/2 | 3 | 1 | 0.3333 |
PCM for three criteria and its priorities
| C5 | C10 | C11 | C12 | C13 | Priority | ||
|---|---|---|---|---|---|---|---|
| Pairwise comparisons of five historical cases with respect to safety | |||||||
| C5 | 1 | 2 | 1/5 | 1/4 | 1/3 | 0.0792 | |
| C10 | 0.5 | 1 | 1/5 | 1/5 | 1/3 | 0.0574 | |
| C11 | 5 | 5 | 1 | 2 | 3 | 0.4230 | |
| C12 | 4 | 5 | 0.5 | 1 | 2 | 0.2785 | |
| C13 | 3 | 3 | 1/3 | 0.5 | 1 | 0.1675 | |
| Pairwise comparisons of five historical cases with respect to cost | |||||||
| C5 | 1 | 2 | 1/3 | 0.5 | 1 | 0.1294 | |
| C10 | 1/2 | 1 | 1/7 | 1/6 | 1/4 | 0.0506 | |
| C11 | 3 | 7 | 1 | 2 | 3 | 0.4204 | |
| C12 | 2 | 6 | 1/2 | 1 | 1 | 0.2314 | |
| C13 | 1 | 4 | 1/3 | 1 | 1 | 0.1719 | |
| Pairwise comparisons of five historical cases with respect to accident loss | |||||||
| C5 | 1 | 2 | 1/3 | 1/3 | 1/2 | 0.1118 | |
| C10 | 1/2 | 1 | 1/4 | 1/3 | 1/2 | 0.0793 | |
| C11 | 3 | 4 | 1 | 2 | 2 | 0.3729 | |
| C12 | 3 | 3 | 1/2 | 1 | 2 | 0.2689 | |
| C13 | 2 | 2 | 1/2 | 1/2 | 1 | 0.1717 | |
PCMs for five historical cases with regard to three criteria and their priority
5. Comparative analysis and discussion
To further verify the validity of the proposed method, the results derived from the proposed method are further compared with other existing case retrieval methods.
First, PCBR is compared with the classic case similarity measurements, such as, ECBR, GCBR RCBR. As can be seen from Example 1, the similarity measurement based on CPT can express the psychological behavior of DM’s preference on distance well. From Table 5, the case similarities and the historical ranking based on CPT is a little different from the three classic case similarity measurements, because it considers the DM’s psychological behavior and can distinguish the DM’s preference strictly. This is more in line with the actual decision situations.
Furthermore, from Table 5, the classic case similarity measurements and PCBR are different, because ECBR considers the distance between two points, GCBR uses the Gaussian function to change the Euclidean distance into nonlinear form, RCBR represents the case similarity using the case correlation, PCBR considers the DM’s psychological behavior. The proposed method aggregates all the advantages of these methods.
The case retrieval method combined with similarity measurement and MCDM has been proposed by Qi et al.12 and Li et al.13 They used the technique for TOPSIS to evaluate the similar historical case set. But [13] pointed out that the TOPSIS has a drawback that the number of cases under evaluation is limited. However, DEA has no limit on the number of DMU and the DEA model has no such restriction. Furthermore, the DEA model not only can solve the situation where one DM gives his/her evaluation for the alternatives by using PCM, but also can solve group decision making and hierarchical structure in the AHP. From Tables 6, 8 and 9, it can be seen that the DEA model can give a best priority vector from a PCM and can help DM to make more accurate decision making.
6. Conclusion
This paper develops a new case retrieval method from a comprehensive view of combining the similarity measurement and DEA model. The primary contributions are summarized as follows:
- (1)
A similarity measurement based on CPT is proposed. This method considers the DM’s psychological behavior and makes the decision result more realistic.
- (2)
The case similarity is gained through the aggregation of four case similarities. This can amplify the advantage of case similarity measurements and overcome the one-sidedness brought about by a single approach.
- (3)
In the case selection, a DEA model is constructed to get the priority vector. It can produce true priority vector for PCM and the DEA model can deal with three formats of evaluations, such as a DM evaluates the alternatives, several DMs evaluate the alternatives and the DM evaluates the alternative from a few criteria. These evaluation formats are usually used very often. So, this DEA model has good usability.
An example about the high-rise fire has shown the necessity of the similarity measurement based on CPT, which considers the DM’s psychological behavior. In addition, the example about the car design has shown the feasibility and validity of the proposed method, which can help DM to find the suitable historical case and to make decision.
For future work, a promising research direction is the use of artificial intelligence method27,28 to improve the validity of the retrieval results. In addition, the case adaptation seems a promising and fruitful research line.
Acknowledgments
We thank two anonymous reviewers for their valuable comments and suggestions which have helped to improve the paper. This work was partly supported by the National Natural Science Foundation of China under the Grant Nos. 71371053 and 61773123, Humanities and Social Science Foundation of Chinese Ministry of Education under the Grant No. 16YJC630008, Fujian Natural Science Foundation of China, No. 2017J01513.
References
Cite this article
TY - JOUR AU - Jing ZHENG AU - Ying-Ming WANG AU - Kai ZHANG PY - 2018 DA - 2018/05/21 TI - A case retrieval method combined with similarity measurement and DEA model for alternative generation JO - International Journal of Computational Intelligence Systems SP - 1123 EP - 1141 VL - 11 IS - 1 SN - 1875-6883 UR - https://doi.org/10.2991/ijcis.11.1.85 DO - 10.2991/ijcis.11.1.85 ID - ZHENG2018 ER -
