2.1. Skill Primitives

We have derived the motion primitives which constitute tasks such as assembly and transport by analyzing a person’s behavior. The motion unit is defined as a “skill” [10–12]. Three basic skills, “move-to-touch,” “rotate-to-level,” and “rotate-to-insert,” are important (Figure 1). The representative person’s behavior can be composed of these three basic skills and similar ones. The units of machine motion can be considered to be similar to the rudiments of human behavior.

Figure 1

Three fundamental skills. (a) Move-to-touch skill. (b) Rotate-to-level skill. (c) Rotate-to-insert skill.

2.2. Stratification of Tasks

In general, it is possible to regard a task performed by a machine as following a hierarchical structure (Figure 2) [10–12]. One tier above the layer “task⁽ⁱ⁾” is the layer “task⁽ⁱ⁺¹⁾”. The “skill” layer is located in the lowest layer, “task⁽⁰⁾”.

Figure 2

Hierarchy of tasks.

3.1. Error Classification

Errors can be classified into several groups based on the possible causes. We consider four error groups: execution, planning, modeling, and sensing (Figure 3) [7–9].

Figure 3

Fundamental process flow with error recovery.

3.2. Error Recovery based on Classification

First, when the error occurs, the cause is estimated. Next, suitable correction of the system is performed based on the tentative cause. The process returns to the previous step, and the task is executed again from this step (Figure 3) [7–9]. The same error is less likely to occur because the corrected process has been executed.

If the scale of the error is small, the process returns to the previous step in the lowest layer of the hierarchy (Figures 3 and 4). Conversely, if the scale of the error is large, the process returns to the previous step in the highest-ranking layer of the hierarchy, and it is executed again from this step (Figure 4).

Figure 4

The expression of task stratification and the process flow of the error recovery.

4.1. Candidate Processes for Recovery

In the previous section, it was shown that the step to which the process returns after failure occurrences alters according to the scale of the error. However, it is possible to return further back than a single step of necessity minimum.

Figure 5 shows various possible error recovery processes for failure occurrences at Subtask_m in Task T [from Start S to Goal G], where Task T consists of sequence [Subtask₁, Subtask₂, Subtask₃, ..., Subtask_m, ..., Subtask_n] and Subtask_k (k = 1, 2, 3, ..., n) consists of sequence [Skill^k₁, Skill ^k₂, Skill ^k₃, ..., Skill ^k_{n_k(max)}]. Subtask_m indicates the minimum traceable unit described in Nakamura et al. [8], i.e., the smallest unit in which it is necessary to return to the first node of a skill primitive sequence if a failure occurs. A skill where a failure occurs is part of the sequence [Skill ^m₁, Skill ^m₂, Skill ^m₃, ..., Skill ^m_{n_k(max)}]. When no problems are encountered, there is possibility that the execution of several skills has continued within Subtask_m, without returning to the previous step immediately after the failure occurrence.

Figure 5

Various processes of error recovery considered for a failure occurred in Subtask_m.

When the process returns to the node before Subtask_j (j is one of 1, 2, 3, …, m), the process [Subtask_j, Subtask_j+1, ..., Subtask_n] is executed in the corrected system (the center bold arrows of Figure 5). However, re-execution using the same sequence of subtasks is not generally possible owing to several factors such as the transformation of the target object and the change of arrangement of the objects. In such a case, the rerun is performed by using an equivalent task of the original sequence of subtasks (the right-side arrows of Figure 5). The equivalent task is derived by large-scale re-planning.

4.2. Selection of the Lowest-cost Process

It is necessary to select one out of the multiple possible error recovery processes. Let us consider that it is most suitable to choose the process with minimum practical costs, where costs include material charges, parts charges, electricity bills, and planning expenses. If failure occurs, error recovery is planned, several task sequences for recovery are derived, these costs are calculated, and the most suitable recovery sequence is then chosen.

5.1. Candidate Processes for Recovery

Let us consider an assembly task in which a nameplate is stuck to a product by four precision screws. Figure 6 shows a sequence of the task. First, a tacking task is performed (Figure 6a–6d) in which these four screws are fastened temporarily to the nameplate, placed levelly; second, an erecting task is performed (Figure 6e and 6f) in which the nameplate with four screws stands up; third, a touching task is performed (Figure 6g and 6h) in which the nameplate is moved to the fixing location; and finally, an installation task is performed (Figure 6i–6m) in which the nameplate is fixed on a plane of the product.

Figure 6

An assembly task in which a nameplate is stuck to a product by four precision screws. (a–d) a tacking task, (e–f) an erecting task, (g–h) a touching task, (i–m) an installation task.

Next, we will consider an error, as shown in Figure 7, in which a precision screw is dropped when a failure occurs at Figure 6h. It is possible to derive various processes for error recovery of this failure. In this example, we consider three types of recovery courses as follows.

Figure 7

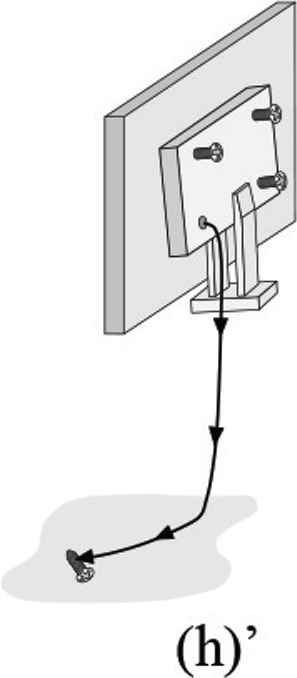
An error in which a screw is dropped at (h) in Figure 6.

• •

  [ER-I] Error Recovery I

  First, we will consider a recovery process that it is easy to understand. The method is rerun from Start S. The nameplate from which one screw in four screws was omitted is discarded, and the re-start is executed using a new nameplate and four new screws, that is, the tacking task (Figure 6a–6d) is performed using new parts.

• •

  [ER-II] Error Recovery II

  Now, we will consider a recovery process carried out by returning to the previous step of a skill primitive (Figure 6d) in the tacking task. Figure 8 shows the process with respect to recovery. The sequence from Figure 8p–8r is an additional process required to return to the previous step. The de-touching task (Figure 8h–8p) and leveling task (Figure 8q and 8r) are performed. It is noted that the sequence from Figure 8d–8m is essentially the same process as that from Figure 6d–6m.

  There are two types of methods for use of a precision screw at the hole of the fallen screw. One is the use of new screw from the parts box, and another is the reuse of the fallen screw by searching and lifting. The former is shown with [ER-II(N)] and the latter with [ER-II(F)].

• •

  [ER-III] Error Recovery III

  For the third process, we will consider the method for a very small scale of return, that is, a recovery process carried out by returning to a skill primitive in Subtask_m of the failure occurrence. The method to immediately rerun the tacking task of a screw at the hole for the fallen screw (Figure 7) in order to regenerate the state of Figure 6h is the easiest to understand. However, we will consider the steady method in which the process of error recovery is carried out after a section Subtask_m of the installation task (Figure 6i–6k) is finished. Figure 9 shows the process with respect to recovery after failure occurrence (Figure 7). Figure 9i–9m corresponds to Figure 7i–7m, respectively. The sequence from Figure 9u and 9v is an additional process to tack a screw into the hole of the nameplate and is performed after the sequence from Figure 9i–9k because of task reliability. In particular, the task to temporarily fasten a screw to the hole of the nameplate is more difficult when the nameplate is fixed perpendicularly than when it is placed levelly.

  There are two types of methods for use of a screw at the hole intended for the fallen screw similar to [ER-II]; [ER-III(N)] and [ER-II(F)] show the methods using a new screw and reusing the fallen screw, respectively.

Figure 8

[ER-II] Error recovery II.

Figure 9

[ER-III] Error recovery III.

5.2. Selection of Recovery Process based on Cost

Next, the calculation of cost is performed for each recovery process. We consider three types of cost: recovery planning cost C(R), object searching cost C(S), and parts purchasing cost C(P). Here, a unit of cost is introduced for simplification; we assume that the fixed number “U” indicates a unit of cost. However, in practical terms, the cost cannot always be related to a fixed value.

First, we consider C(R), which represents the cost generated by the process added with a recovery. The C(R) value of [ER-I] is smaller because it follows the same sequence to the original, and conversely, that of [ER-III] is larger because it follows a sequence with a difficult skill primitive. We suppose that C(R) of [ER-I] = U, C(R) of [ER-II] = 2U, and C(R) of [ER-III] = 3U.

Second, we consider C(S), which represents the cost generated by the process added for finding a screw. Then, let us assume that [Sch-N] indicates the process of finding a new screw in the parts box, and [Sch-F] indicates the process of finding the fallen screw in the working environment. The C(S) value of [Sch-N] is smaller than that of [Sch-F], and thus, we suppose that C(S) of [Sch-N] = 2U, and C(S) of [Sch-F] = 5U.

Third, we consider C(P), which represents the cost generated by the purchase of parts. Then, let us assume that [Pch-S] indicates the purchase expense of a new screw, and [Pch-P] indicates the purchase expense of a new nameplate with four new screws. The C(P) value of [Pch-P] is significantly larger than that of [Pch-S], and thus, we suppose that C(P) of [Pch-S] = U, and C(P) of [Pch-P] = 8U.

We now calculate a cost for each case, considering the total cost TC = C(R) + C(S) + C(P).

The following relation is derived from Equations (1) by (5).

Thus, TC [ER-II (N)] will have the smallest price, indicating that the case of [ER-II] Error Recovery II with use of a new screw instead of the dropped screw has the lowest cost.