X-means Clustering for Wireless Sensor Networks
- DOI
- 10.2991/jrnal.k.200528.008How to use a DOI?
- Keywords
- K-means; X-means; clustering; wireless; sensors; networks
- Abstract
K-means clustering algorithms of wireless sensor networks are potential solutions that prolong the network lifetime. However, limitations hamper these algorithms, where they depend on a deterministic K-value and random centroids to cluster their networks. But, a bad choice of the K-value and centroid locations leads to unbalanced clusters, thus unbalanced energy consumption. This paper proposes X-means algorithm as a new clustering technique that overcomes K-means limitations; clusters constructed using tentative centroids called parents in an initial phase. After that, parent centroids split into a range of positions called children, and children compete in a recursive process to construct clusters. Results show that X-means outperformed the traditional K-means algorithm and optimized the energy consumption.
- Copyright
- © 2020 The Authors. Published by Atlantis Press SARL.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
Machine-to-machine communication and internet of things require low power communication networks [1]. Wireless Sensor Network (WSN) is a potential candidate that provides an infrastructure for these technologies. WSN is a group of wireless nodes that are equipped with sensors and actuators; the network is designed as an application specific and performs dedicated tasks. Wireless nodes depend on batteries as a source of energy and the wireless unit drains nodes batteries [2]; therefore, routing data considered an expensive and complex task. In the literature, clustering routing algorithms have shown promising enhancements of the WSN lifetime; classical algorithms such as LEACH [3], HEED [4], and EECS [5] divide their networks into random clusters, and each cluster comprises a Cluster Head (CH) and wireless nodes. Data collected from surroundings and relayed to CHs; then CHs have to forward the data after aggregating them to a central unit called Sink. CHs use long-range communications called backhauling to the sink. The role of CH is frequently rotated to distribute the energy consumption load among nodes and thus re-clustering initiated every round of operation. Due to the random clustering of wireless nodes, classical algorithms suffer from an unbalanced intra-cluster distance and unbalanced energy consumptions. Another clustering algorithms are K-means algorithms such as Periyasamy et al. [6], Park et al. [7], Sasikumar and Khara [8], Razzaq et al. [9] and Khan et al. [10]; these algorithms estimate the number of clusters and their initial centroids. In K-means, wireless nodes assigned to clusters based on the minimum distance to centroids, then average Euclidean distance to these centroids are determined and centroids repositioned. After that, wireless nodes re-clustered and assigned to the new centroids. Determining the mean distance and re-clustering the nodes are repeated until centroid positions fixed, and cluster members are static.
Unlike classical algorithms, K-means algorithms balance the intra-cluster distance of clusters; but still these algorithms construct unequal clusters because of random centroid positions; where a bad choice of initial centroids leads to unbalanced cluster sizes and unbalanced CHs consumption, thus premature CHs death at the early stage of the network lifetime. Therefore, this article proposes to construct initial clusters using K-means, then the X-mean algorithm splits each cluster centroid into multiple positions, and then searches for the best position and the best number of clusters.
The rest of the article is as follows, in Section 2 the system model is presented, then in Section 3 we propose X-mean algorithm and describe its two operation phases with mathematical equations, after that in Section 4 the simulation results and a discussion on how the proposed algorithm prolongs WSN lifetime, finally in Section 5, we conclude our work with future recommendations to further enhance the X-means algorithm.
2. SYSTEM MODEL
The system model obtained from Ref. [3], and it includes two parts; a transmitter model and a receiver model, as in Equations (1) and (2). The transmitter consumption model of Equation (1) consists of Eelec as the energy required to aggregate and process data, and the amplification energy required to transmit data (b) over (d) distance. Equation (1) describes two types of the amplification energies, where εfs describes the amplification energy required to transmit a single bit using the freespace model; and εmp describes the amplification energy required to transmit a single bit using the multipath fading model. d0 is the crossover distance between the freespace model and the multipath model, and it is described in Park et al. [7]. The total transmission energy (ETx) is proportional to the distance between a source node and a destination node, where it corresponds to d2 attenuation when d is less than d0 and corresponds to d4 attenuation when d is greater than or equal d0. The Receiving consumption (ERx) includes the energy required to process data packet (b) in bits as in Equation (2).
3. PROPOSED METHOD
In our previous work [11], X-means had a fixed number of children, but here the X-means provides a dynamic range of centroids. The concept of the X-means clustering summarized into two phases; the first phase is constructing random clusters with random centroids, then using K-means, optimize these positions as in Equation (3). The process repeated recursively until a final copy of centroids is determined and the final copy of centroids called parent centroids. In phase two, parents give birth to multiple children (Cj), the initial locations of the children determined as in Equation (4); where θ = 2π/j and (dm) is the average Euclidean distance between the parent and nodes in the cluster as in Equation (5).
Pn: Parent (n) centroid.
αn–1(x, y): x and y position of previous (n − 1) parent centroid.
Sn: Set of nodes assigned to Pn.
βi(x, y): the x and y position of node (i).
dm: the average distance between parent centroid and nodes in the cluster.
Cj: the location of the child (j) of parent (Pn).
After that, new children Cj are set as cluster centroids, then nodes re-clustered and assigned using a minimization technique, where nodes grouped by the minimum average some of their distance from the sink and children (Cj) as in Equations (6) and (7). The X-means algorithm recursively executes Equation (8) until children centroid positions are fixed. The recursive run has three outcomes; children form their own clusters and parents collapsed, second some children and parents diminished, and third, children collapsed, and parents repositioned to best locations.
CCnj: final position of child (j) of parent (n).
∅(x, y): position of the sink.
ADij: average distance to the child (j) and the sink.
ADi: minimum average distance of node (i) to child (j).
dij: node (i) Euclidean distance to child (j).
Disink: node (i) Euclidean distance to the sink.
Figure 1 shows an example of the algorithm run in an area of 100 × 100, where parents set to three and children to two. The first generation is parents generated by K-means as in Figure 1a, and the number of generated parents is three, then parents split and each gives birth to two children as in Figure 1b (marked with triangle and circles), the total of children and parents becomes nine centroids, finally X-means diminishes the parents, and some children, and repositioned the remaining children as in Figure 1c. Remaining centroids form static clusters of the network. In X-means, nodes with minimum distance to centroids and highest energy selected as CHs, then if the CH energy dropped below an energy threshold, it steps down and the next closest and highest energy node becomes the CH. In our implementation, the energy threshold is a predefined value, but this value is not static, where once a node energy dropped below the threshold the node determines a new threshold, the new threshold is a step down from the original threshold by (σ ) as in Equation (9).
Eth(n): the new energy threshold.
Eth(n − 1): the previous energy threshold.
This step down ensures that all cluster members can participate as CHs until they are depleted.
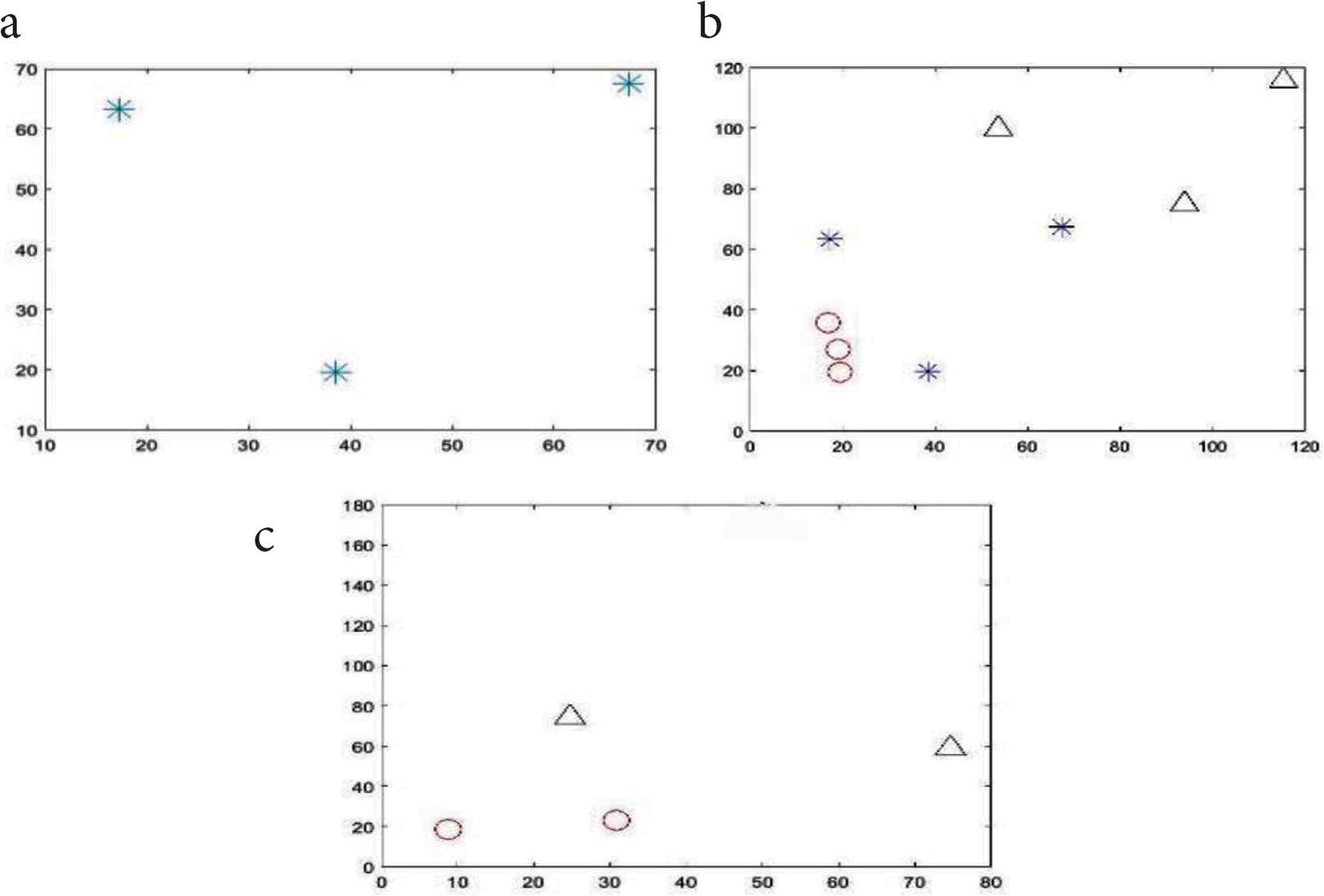
X-means two phase of centroid generation. (a) Parent centroids generated after running K-means. (b) Parents give birth to new children centroids. (c) Remaining centroids after running X-means.
4. RESULTS AND DISCUSSION
The proposed algorithm simulated with MATLAB and the simulation parameters in Table 1. There are extensive simulations done to test the algorithm. Figure 2 depicts the result of an area 220 × 220 that contains 220 nodes, nodes deployment is random, but nodes density is uniform. In X-means the number of centroids is not determined, but only initial centroids are set. Assuming the maximum allowed clusters is 5% of the total network nodes [3], then the total clusters are 11, thus the X-means initialized for two scenarios; when the number of parents (P) is two and give birth to five children (C), and when P is five and give birth to two C; also, K-means [7] initialized for ten centroids. During the simulation, the adopted data paradigm is continuous, where CHs always have data to send to the sink. Results measure the network lifetime in round, where a single round is a single packet received from CHs at the sink.
| Parameter | Description | Value |
|---|---|---|
| d0 | Crossover distance | 87 m |
| εfs | Freespace model amplification energy | 10 pJ/bit/m2 |
| εmp | Multipath amplification energy | 0.0013 pJ/bit/m4 |
| Eelec | Single bit processing energy | Tx or Rx = 50 nJ/bit |
| Aggregation = 5 nJ/bit | ||
| Einit | Initial energy | 0.5 J |
| Eth | Energy threshold | 0.2 J |
| σ | Eth step down | 5% |
| Packet size | Data size | 4.2 Kb/packet |
| Control packet | Packet headers | 0.2 Kb/packet |
X-means simulation parameters
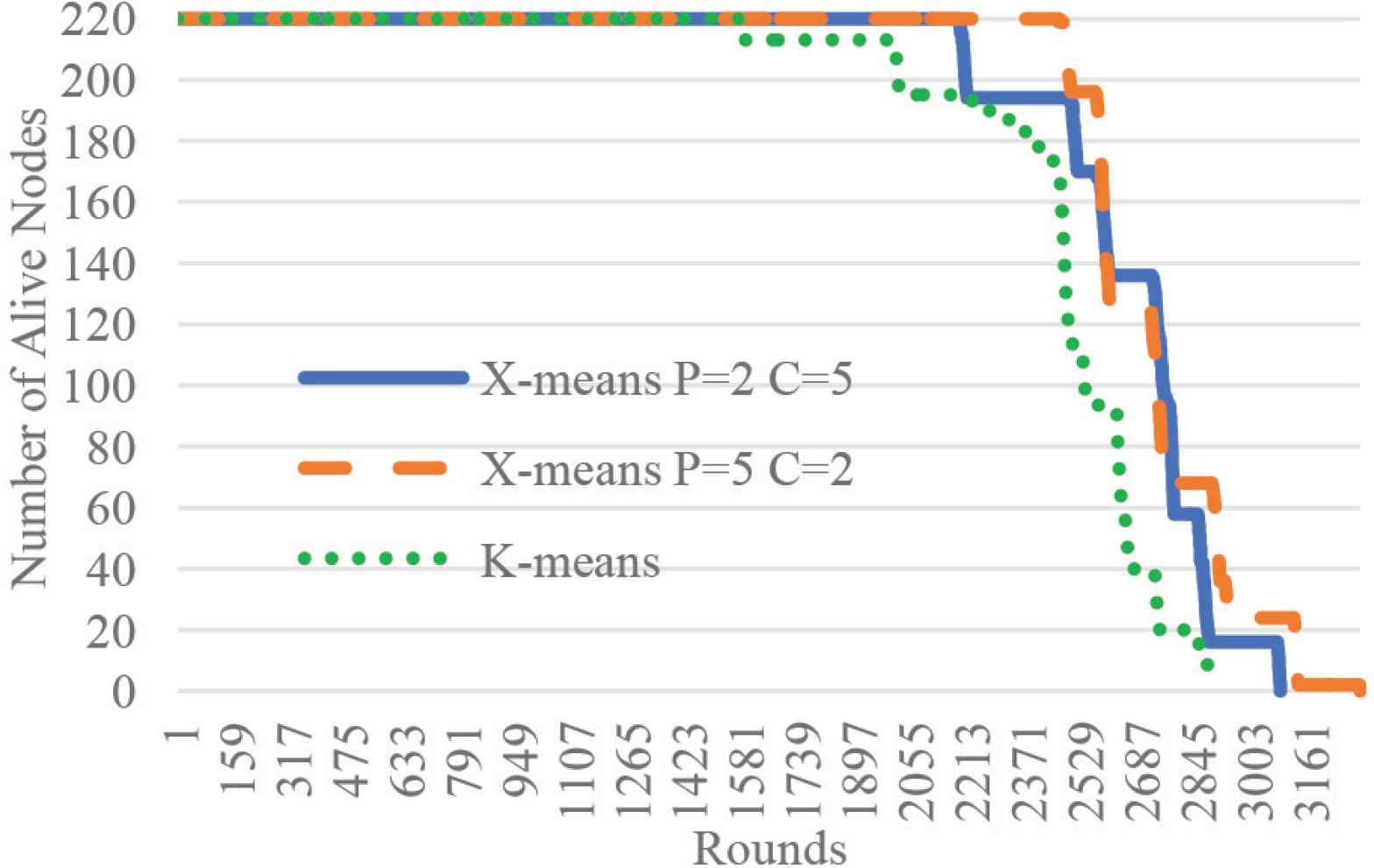
X-means simulation when the number of parents is two and five and children two and five.
Results show that X-means prolongs the network life in term of First Node Death (FND). The positions of centroids minimized nodes consumption per round by reducing the intra-cluster distance. The result in Figure 2, shows FND enhancement of 39% when P = 2 and 57% when P = 5 over the K-means algorithm. We extended the simulation to include variations of the network areas and combinations of parents and children, the results depicted in Figure 3. The result shows that whenever the number of parents is greater than the number of children, X-means achieves a smaller intra-cluster distance. This phenomenon occurs because of dividing the area into small search spaces at phase one of the algorithm, which makes it easier to find the best position at phase two. During the simulation we also monitored the average energy consumption as in Figure 4. The result shows that the X-means in its all variation consumed energy less than K-means. The highest X-means consumption occurred when the area was 370 × 370, where increasing the area increased the backhaul distance and thus increased the overall energy consumption of the cluster.
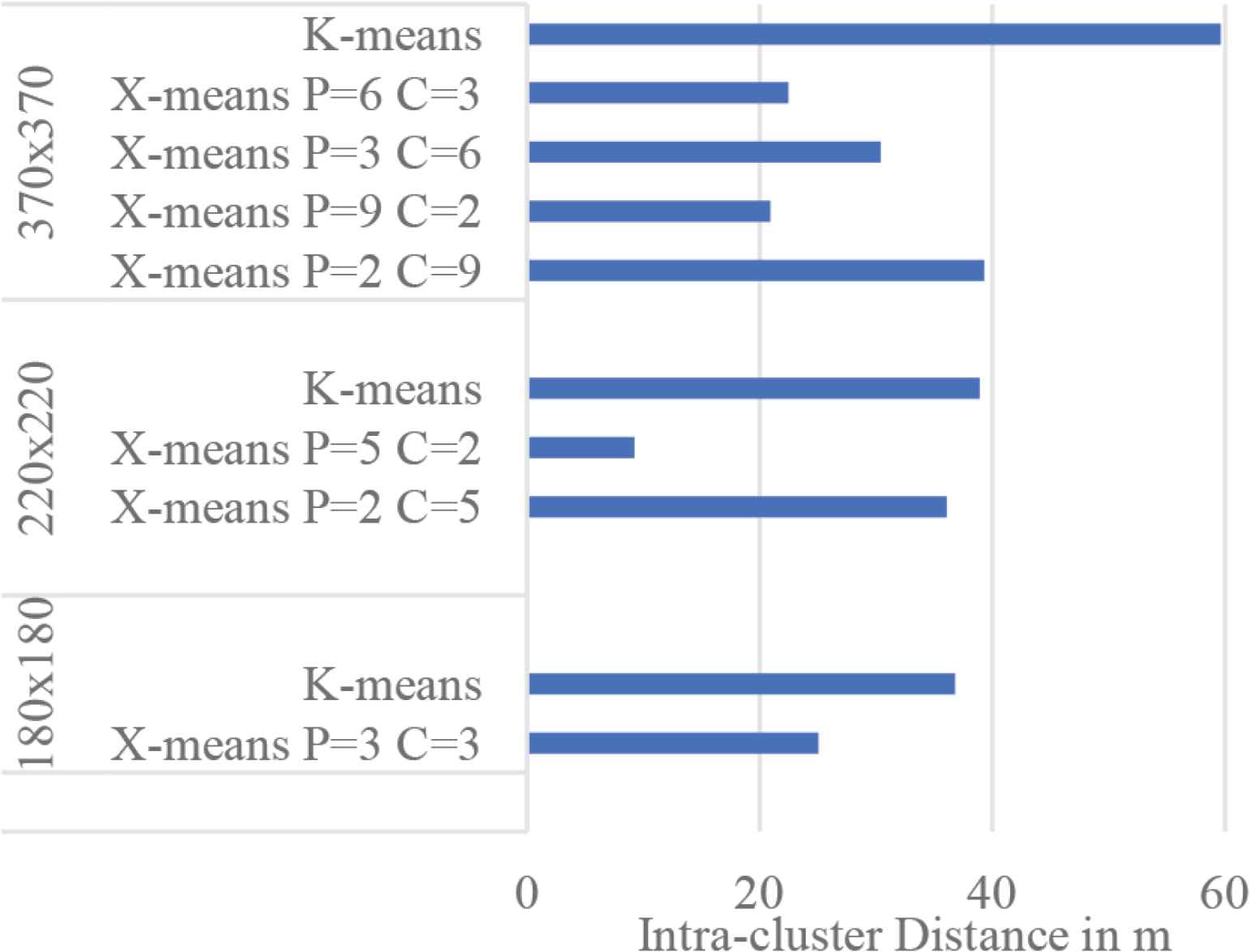
Intra-cluster distance for variations of the network areas.

Average energy consumption for the cluster per round of the simulation.
5. CONCLUSION
In this article we proposed the X-means with multiple children as a solution for K-means shortcomings. The algorithm depends on the initial values of parents and children. Then parents and children evaluated to generate a final copy of centroids that is less than the maximum number of the allowed network centroids. X-means selects centroid locations that optimize the intra-cluster distance and prolong the network lifetime. The simulation scenarios were limited to 180, 220 and 370 nodes. Thus, the performance is not checked for large scale deployment such as 1000 nodes.
CONFLICTS OF INTEREST
The authors declare they have no conflicts of interest.
ACKNOWLEDGMENTS
The authors thank UCSI University Trust Fund and Centre of Excellence for Research, Value Innovation and Entrepreneurship (CERVIE) for supporting this work.
AUTHORS INTRODUCTION
Abdelrahman Radwan
 He obtained a BEE (2007) and M.Sc (2009) from Northumbria University, UK. From 2010 to 2016, he worked as a senior wireless development engineer. Currently, he is a PhD student in Engineering Department at UCSI University, Malaysia. His research interests are wireless systems and embedded systems.
He obtained a BEE (2007) and M.Sc (2009) from Northumbria University, UK. From 2010 to 2016, he worked as a senior wireless development engineer. Currently, he is a PhD student in Engineering Department at UCSI University, Malaysia. His research interests are wireless systems and embedded systems.
Dr. Nazhatul Hafizah Kamarudin
 She is currently a lecturer in Department of Electrical and Electronic in UCSI University in Malaysia. She is also the UCSI Internship Coordinator. She graduated with a bachelor degree and master degree in Electrical Engineering with honour from Stevens Institute of Technology, NJ, USA. She received her PhD in Electrical Engineering at UiTM Shah Alam, Malaysia. Her research works focus on Cybersecurity, Wireless Sensor Network and the applications of Artificial Intelligence (AI). Her research on Mobile E-Health Authentication Scheme for EHEART Application is chosen to be among the top three selected researches in Asia-Pacific Economic Cooperation (APEC) Policy Partnership on Science, Technology and Innovation in 2017.
She is currently a lecturer in Department of Electrical and Electronic in UCSI University in Malaysia. She is also the UCSI Internship Coordinator. She graduated with a bachelor degree and master degree in Electrical Engineering with honour from Stevens Institute of Technology, NJ, USA. She received her PhD in Electrical Engineering at UiTM Shah Alam, Malaysia. Her research works focus on Cybersecurity, Wireless Sensor Network and the applications of Artificial Intelligence (AI). Her research on Mobile E-Health Authentication Scheme for EHEART Application is chosen to be among the top three selected researches in Asia-Pacific Economic Cooperation (APEC) Policy Partnership on Science, Technology and Innovation in 2017.
Dr. Mahmud Iwan Solihin
 He is an Assistant Professor in Mechatronics Engineering Department, specialized in applications of artificial intelligence/machine learning, optimizations, control systems, robotics and automation. His current research interest is mainly on applications of artificial intelligence (AI) and optimization algorithms in various field including robotics, control systems, spectroscopy applications, sensor networks, etc., toward sustainable Engineering development in the future.
He is an Assistant Professor in Mechatronics Engineering Department, specialized in applications of artificial intelligence/machine learning, optimizations, control systems, robotics and automation. His current research interest is mainly on applications of artificial intelligence (AI) and optimization algorithms in various field including robotics, control systems, spectroscopy applications, sensor networks, etc., toward sustainable Engineering development in the future.
Dr. Emily Leong Hung Yang
 She is currently a Lecturer in Department of Electrical and Electronic in UCSI University in Malaysia. She is the Honorary Secretary of IET Malaysia Local Network for 2018–2020. She graduated with a degree in Electrical Engineering with first class honour from University Malaya and subsequently received her PhD in Engineering at UNITEN, Malaysia. Her research works focus on IC microelectronics enhance packaging, IR 4.0, wireless sensor network and image processing. She also has over 9 years of experience in multinational semiconductor companies before joining academic line.
She is currently a Lecturer in Department of Electrical and Electronic in UCSI University in Malaysia. She is the Honorary Secretary of IET Malaysia Local Network for 2018–2020. She graduated with a degree in Electrical Engineering with first class honour from University Malaya and subsequently received her PhD in Engineering at UNITEN, Malaysia. Her research works focus on IC microelectronics enhance packaging, IR 4.0, wireless sensor network and image processing. She also has over 9 years of experience in multinational semiconductor companies before joining academic line.
Dr. M. Rizon
 He graduated Doctor of Engineering at Department of Computer Science and Intelligence System in Oita University, Japan. He was a Professor of Biomedical Technology in King Saud University, Saudi Arabia in 2010. He served at MIEC, Fuzhou University, China in 2019. Currently, he is a Professor at Department of Electrical and Electronics, UCSI University, Malaysia. He is a member of MIET and MIEM.
He graduated Doctor of Engineering at Department of Computer Science and Intelligence System in Oita University, Japan. He was a Professor of Biomedical Technology in King Saud University, Saudi Arabia in 2010. He served at MIEC, Fuzhou University, China in 2019. Currently, he is a Professor at Department of Electrical and Electronics, UCSI University, Malaysia. He is a member of MIET and MIEM.
Dr. Hazry Desa
 He received his Bachelor of Mechanical Engineering from Tokushima University, Japan. He was a Senior Design Mechanical Engineer in R&D Sony Technology Malaysia in 1997. In 2001 he was employed by Tamura Electronics Malaysia. He pursued his PhD at the Artificial Life and Robotics Laboratory, Oita University, Japan in 2003. He is a Professor, Director of Center of Excellence for Unmanned Aerial System at University of Perlis. He is a SMIEEE, MIET and registered as Professional Technologist.
He received his Bachelor of Mechanical Engineering from Tokushima University, Japan. He was a Senior Design Mechanical Engineer in R&D Sony Technology Malaysia in 1997. In 2001 he was employed by Tamura Electronics Malaysia. He pursued his PhD at the Artificial Life and Robotics Laboratory, Oita University, Japan in 2003. He is a Professor, Director of Center of Excellence for Unmanned Aerial System at University of Perlis. He is a SMIEEE, MIET and registered as Professional Technologist.
Dr. Muhammad Azizi Bin Azizan
 He is a Lecturer in Faculty of Engineering Technology at uniMAP. He holds B.Sc and M.Sc degree from UiTM. He is a member of (CIOB), (RISM), (MBOT) and certified trainer of HRDF. His research and teaching interests are management issues in built environment/engineering projects, sustainable and development. He is Co-Founder of Haas Solutions Sdn Bhd and holds the equity in Haas Engineering Sdn Bhd and Braintree Scientific Resources where the companies run the technology development activities eg. Drones, Data Processing, Data Mining and Laboratory Testing.
He is a Lecturer in Faculty of Engineering Technology at uniMAP. He holds B.Sc and M.Sc degree from UiTM. He is a member of (CIOB), (RISM), (MBOT) and certified trainer of HRDF. His research and teaching interests are management issues in built environment/engineering projects, sustainable and development. He is Co-Founder of Haas Solutions Sdn Bhd and holds the equity in Haas Engineering Sdn Bhd and Braintree Scientific Resources where the companies run the technology development activities eg. Drones, Data Processing, Data Mining and Laboratory Testing.
REFERENCES
Cite this article
TY - JOUR AU - Abdelrahman Radwan AU - Nazhatul Kamarudin AU - Mahmud Iwan Solihin AU - Hungyang Leong AU - Mohamed Rizon AU - Hazry Desa AU - Muhammad Azizi Bin Azizan PY - 2020 DA - 2020/06/02 TI - X-means Clustering for Wireless Sensor Networks JO - Journal of Robotics, Networking and Artificial Life SP - 111 EP - 115 VL - 7 IS - 2 SN - 2352-6386 UR - https://doi.org/10.2991/jrnal.k.200528.008 DO - 10.2991/jrnal.k.200528.008 ID - Radwan2020 ER -
