A Multi-agent Reinforcement Learning Method for Role Differentiation Using State Space Filters with Fluctuation Parameters
- DOI
- 10.2991/jrnal.k.210521.002How to use a DOI?
- Keywords
- Reinforcement learning; role differentiation; meta-parameter; waveform changing; state space filter
- Abstract
Recently, there have been many studies on Multi-agent Reinforcement Learning (MARL) in which each autonomous agent obtains its own control rule by RL. Here, we hypothesize that different agents having individuality is more effective than uniform agents in terms of role differentiation in MARL. We have previously proposed a promoting method of role differentiation using a waveform changing parameter in MARL. In this paper, we confirm the effectiveness of role differentiation by introducing the waveform changing parameter into a state space filter through computational examples using “Pursuit Game” as a multi-agent task.
- Copyright
- © 2021 The Authors. Published by Atlantis Press B.V.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
Engineers and researchers are paying more attention to Reinforcement Learning (RL) [1] as a key technique for realizing computational intelligence such as adaptive and autonomous decentralized systems. Recently, there have been many studies on Multi-agent Reinforcement Learning (MARL) in which each autonomous agent obtains its own control rule by RL. We hypothesize that different agents having individuality is more effective than uniform agents in terms of role differentiation in MARL. Here, we define “individuality” in this paper as being able to be externally observed, but not a difference that we are incapable observing, such as a difference of internal construction.
We have been exploring the assertion that differences in interpretations of experiences in the early stages of learning have a great effect on the creation of individuality of autonomous agents. To produce differences in interpretations of the agents’ experiences, we have utilized Beck’s “Cognitive distortions” [2], which is a form of cognitive therapy.
We then proposed a “fluctuation parameter” which is a wave-form changing meta-parameter to realize “Disqualifying the positive” which is one of the “Cognitive distortions”, and a promoting method of role differentiation using the fluctuation parameter in MARL [3].
In this paper, we introduce the “fluctuation parameter” into a state space filter [4] to realize “Overgeneralizing” which is one of the “Cognitive distortions”, and confirm the effectiveness of role differentiation by introducing the fluctuation parameter into the state space filter through computational examples using “Pursuit Game” as a multi-agent task.
2. Q-LEARNING
In this section, we introduce Q-Learning (QL) [5] which is one of the most popular RL methods. QL works by calculating the quality of a state-action combination, namely the Q-value, that gives the expected utility of performing a given action in a given state. By performing an action a ∈ AQ, where AQ ⊂ A is the set of available actions in QL and A is the action space of the RL agent, the agent can move from state to state. Each state provides the agent with a reward r. The goal of the agent is to maximize its total reward.
The Q-value is updated according to the following Equation (1), when the agent is provided with the reward:
The agent selects an action according to the stochastic policy π(a|s), which is based on the Q-value. π(a|s) specifies the probabilities of taking each action a in each state s. Boltzmann selection, which is one of the typical action selection methods, is used in this research. Therefore, the policy π(a|s) is calculated as
3. STATE SPACE FILTER FOR REINFORCEMENT LEARNING
We have proposed a state space filter based on the entropy which is defined by action selection probability distributions in a state [4].
The entropy of action selection probability distributions using Boltzmann selection in a state H(s) is defined by
The state space filter is adjusted by treating this entropy H(s) as an index of a correctness of state aggregation in the state s. In particular, in case of mapping the input state space roughly to the state space, a perceptual aliasing problem can occur. That is, the action which an agent should select cannot be identified clearly. Thus, the entropy may not be small enough in a state and state space should be divided. In this paper, sufficiency of the number of learning opportunities is judged using a threshold value θL.
Therefore, due to a perceptual aliasing problem having occurred, if the entropy does not get smaller than a threshold value θH despite the number of learning opportunities being sufficient, the state space filter is adjusted by dividing the state.
Similarly, due to the states being too divided, if the entropy is smaller than θH in a state s and a different state mapping from a transited input state s′, and representative actions in each other’s states are the same, the state space filter is adjusted by integrating the states.
4. FLUCTUATION PARAMETER
Reinforcement learning has meta-parameters κ to determine how RL agents learn control rules. The meta-parameters κ include the learning rate α, the discount factor β, ε of ε -greedy which is one of the action selection methods, and the temperature τ of Boltzmann action selection method.
In this paper, the following fluctuation parameter using damped vibration function is introduced into this κ.
5. COMPUTATIONAL EXAMPLES
5.1. Pursuit Game
The effectiveness of the proposed approach is investigated in this section. It is applied to the so-called “Pursuit Game” where three RL agents move to capture a randomly moving target object in a discrete 10 × 10 globular grid space. Two or more agents or an agent and the target object cannot be located at the same cell. At each step, all agents simultaneously take one of the five possible actions: moving north, south, east, west or standing still. A target object is captured when all agents are located in cells adjacent to the target object and surrounding the target object in three directions.
The agent has a field of view, and the depth of view is set at 3. Therefore, the agent can observe the surrounding (3 × 2 + 1)2 − 1 cells. The agent determines the state by information within the field of view.
The positive reinforcement signal rt = 10 (reward) is given to all agents only when the target object is captured, and the positive reinforcement signal rt = 1 (sub reward) is given to the agent only when the agent is located in the cell adjacent to the target object, and the reinforcement signal rt = 0 is given at all other steps. The period from when all agents and the target object are randomly located at the start point to when the target object is captured and all agents are given a reward, or when 100,000 steps have passed is labeled 1 episode. The period is then repeated.
5.2. Setting of Reinforcement Learning Agents
All agents observe the target object only to confirm the effectiveness of role differentiation, e.g. moving east of the target object. Therefore, the state space is constructed with a 1-dimensional space.
Computational examples have been done with parameters as shown in Table 1. In addition, all initial Q-values are set at 5.0 as the optimistic initial values, and θH was set referring to about 0.288: the maximal value of the entropy when the highest selection probability for one action is 0.9.
| Parameter | Value |
|---|---|
| αQ | 0.1 |
| γ | 0.9 |
| τ | 0.1 |
| θH | 0.3 |
| θL | 1000 |
Parameter setting of Q-learning with a state space filter
5.3. Example (A): Introducing the Fluctuation Parameters into the Learning Rate
The effectiveness of role differentiation by introducing the three fluctuation parameters, in which the initial phase ϕ = 0, the amplitude A = 0.09, and the wavelength λ = {50, 100, 500}[episode], into the learning rate of QL with the state space filter (hereafter called “50”, “100”, and “500”, respectively) is investigated in comparison with an ordinary QL with the state space filter without fluctuation parameter (hereafter called “constant”). Here, the fluctuation parameters of all agents take the same value. The unit of the phase tp is set [episode] which is the same as the wavelength λ, the unit of the damped phase tpa is set [episode], and the initial phase of damping is set at tps = 250 [episode]. The range of values which the fluctuation parameter for αQ = 0.1 can take e.g. [0.01, 0.19] on the condition of A = 0.09.
The average numbers of steps and the average size of the state space required to capture the target object were observed during learning over 20 simulations with various wavelength parameters in the learning rate, as described in Figures 1 and 2, respectively.
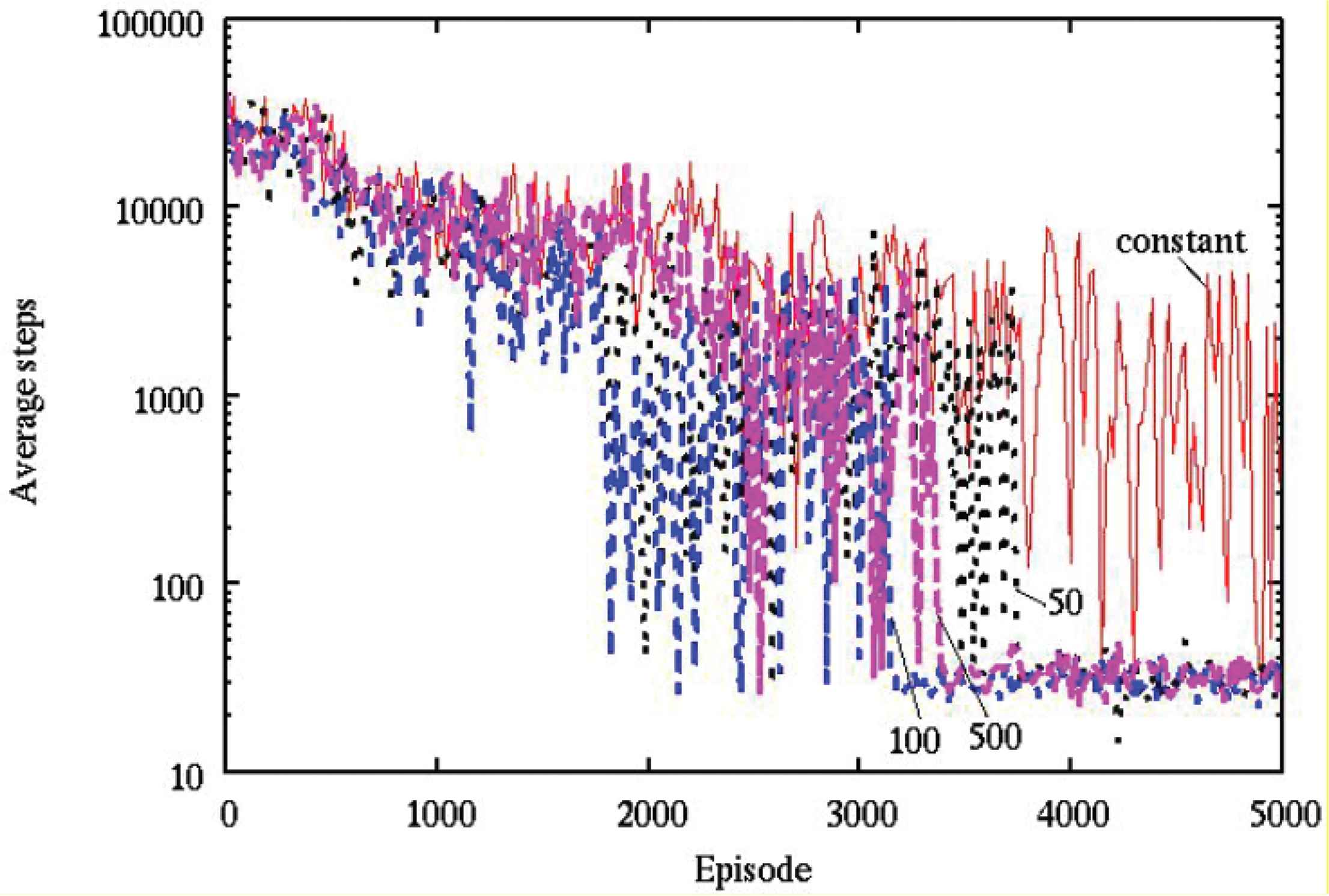
The average number of steps by various wavelength parameters in the learning rate (ϕ = 0 [rad]).
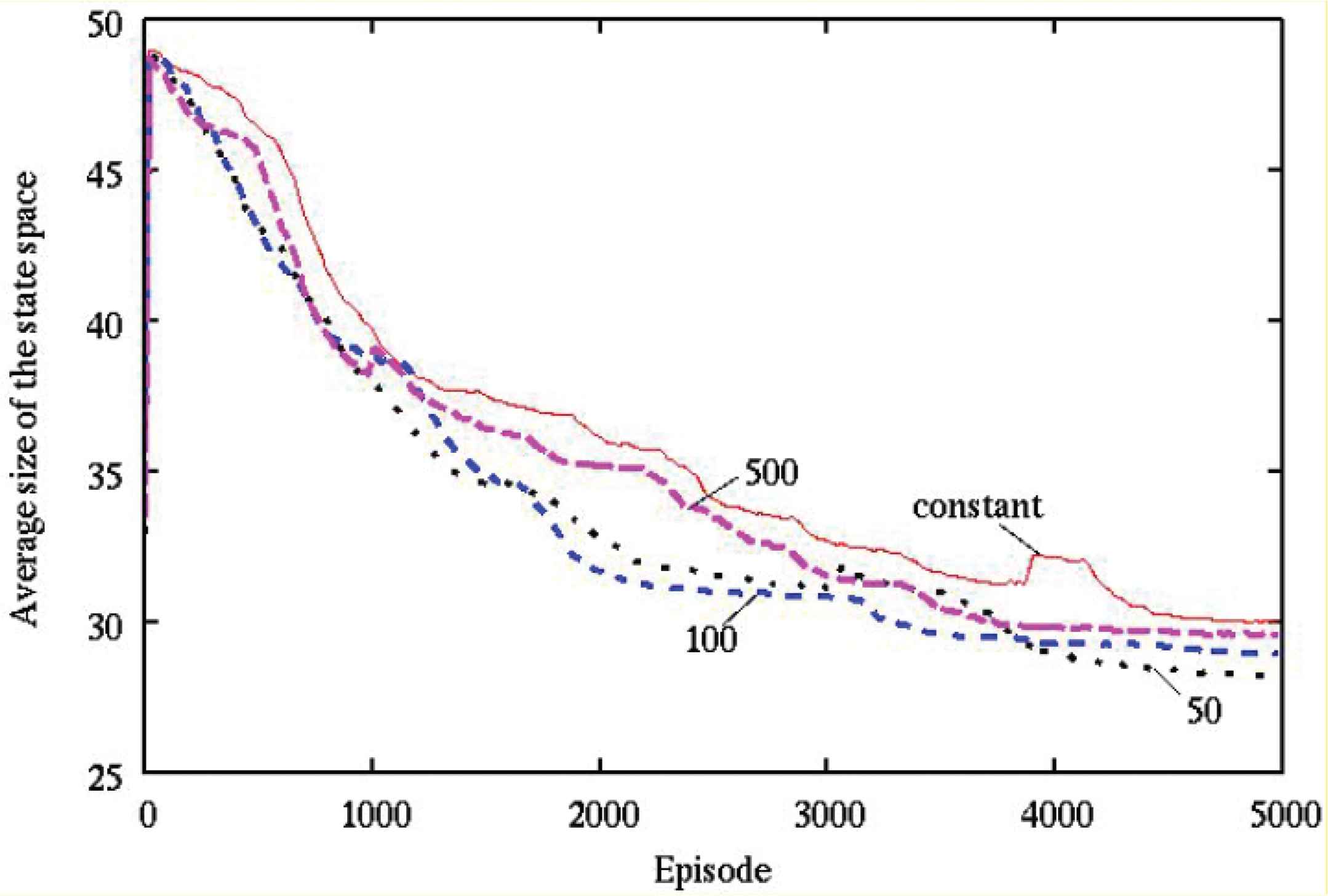
The average size of the state space by various wavelength parameters in the learning rate (ϕ = 0 [rad]).
It can be seen from Figures 1 and 2 that, (1) “50”, “100” and “500” show a better performance than “constant” with regard to the obtained control rule, (2) “50”, “100” and “500” are smaller than “constant” with regard to the size of the state space.
5.4. Example (B): Introducing the Fluctuation Parameters into the Temperature
The effectiveness of role differentiation by introducing the three fluctuation parameters, in which the initial phase ϕ = 0, the amplitude A = 0.09, and the wavelength λ = {50, 100, 500}[episode], into the temperature of Boltzmann action selection method (hereafter called “50”, “100”, and “500”, respectively) is investigated in comparison with an ordinary QL with the state space filter without fluctuation parameter (hereafter called “constant”). Here, the fluctuation parameters of all agents take the same value. The unit of the phase tp is set [episode] which is the same as the wavelength λ, the unit of the damped phase tpa is set [episode], and the initial phase of damping is set at tps = 250 [episode]. The range of values which the fluctuation parameter for τ = 0.1 can take e.g. [0.01, 0.19] on the condition of A = 0.09. If the temperature is zero, then action selection of the agent is greedy and situations where agents cannot capture the target object occur. Therefore, A is set at 0.09.
The average numbers of steps and the average size of the state space required to capture the target object were observed during learning over 20 simulations with various wavelength parameters in the temperature, as described in Figures 3 and 4, respectively.
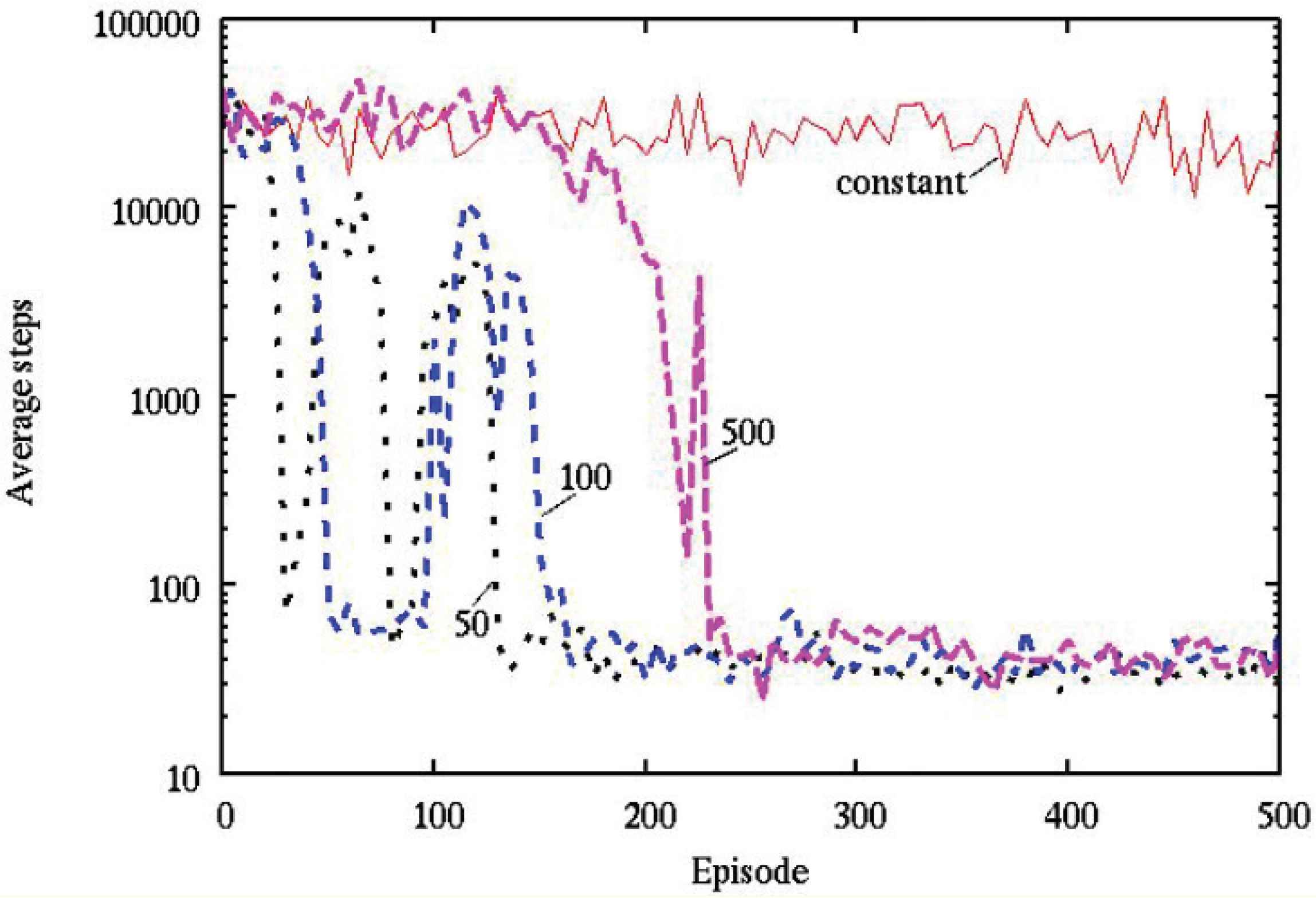
The average number of steps by various wavelength parameters in the temperature (ϕ = 0 [rad]).
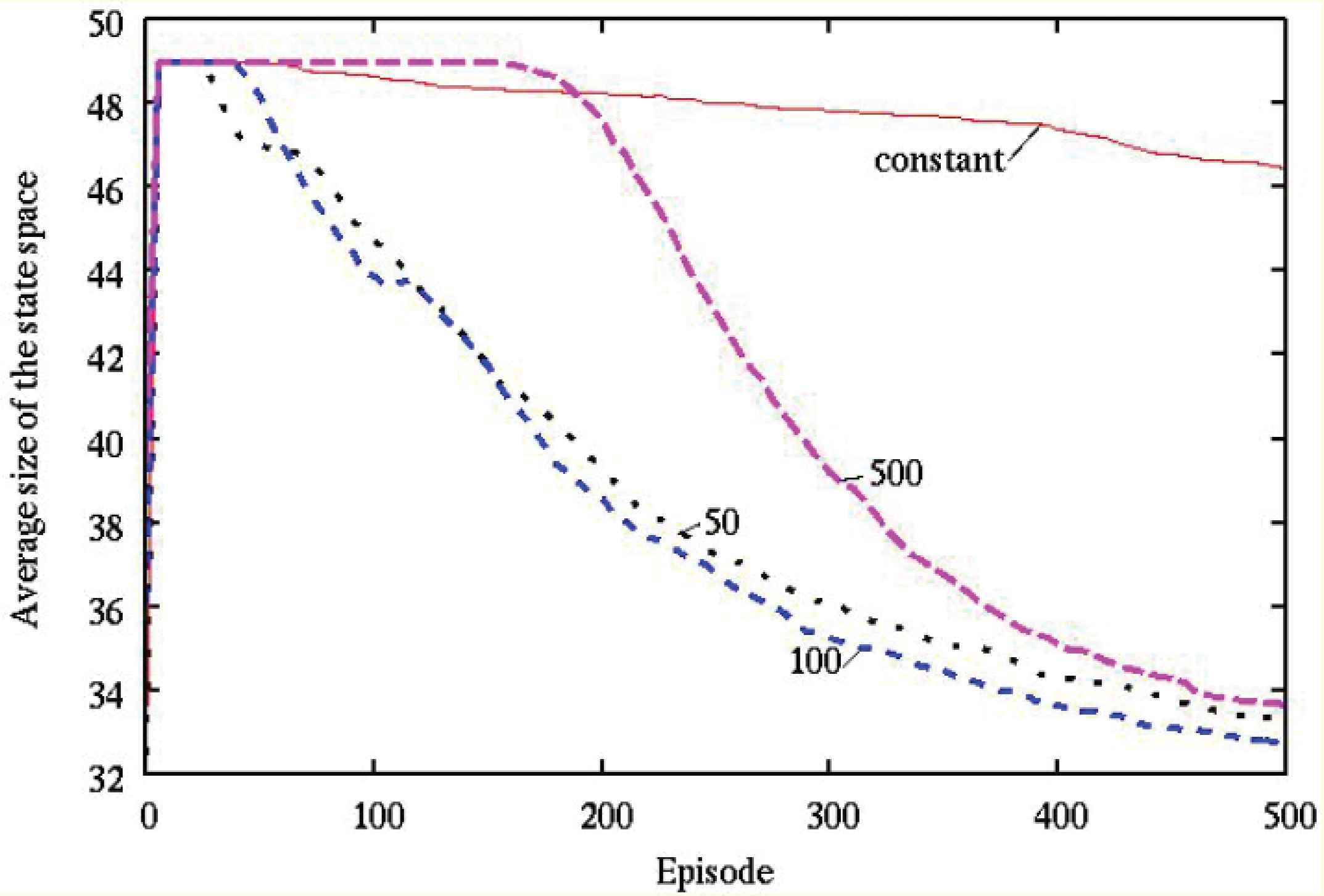
The average size of the state space by various wavelength parameters in the temperature (ϕ = 0 [rad]).
It can be seen from Figures 3 and 4 that, (1) “50”, “100” and “500” show a better performance than “constant” with regard to the obtained control rule, (2) “50”, “100” and “500” are smaller than “constant” with regard to the size of the state space.
An example of obtained state space filters where wavelength λ = 50 [episode] in 1000 episode is described in Figure 5. It can be seen from Figure 5 that each agent divided different respective area into smaller parts.
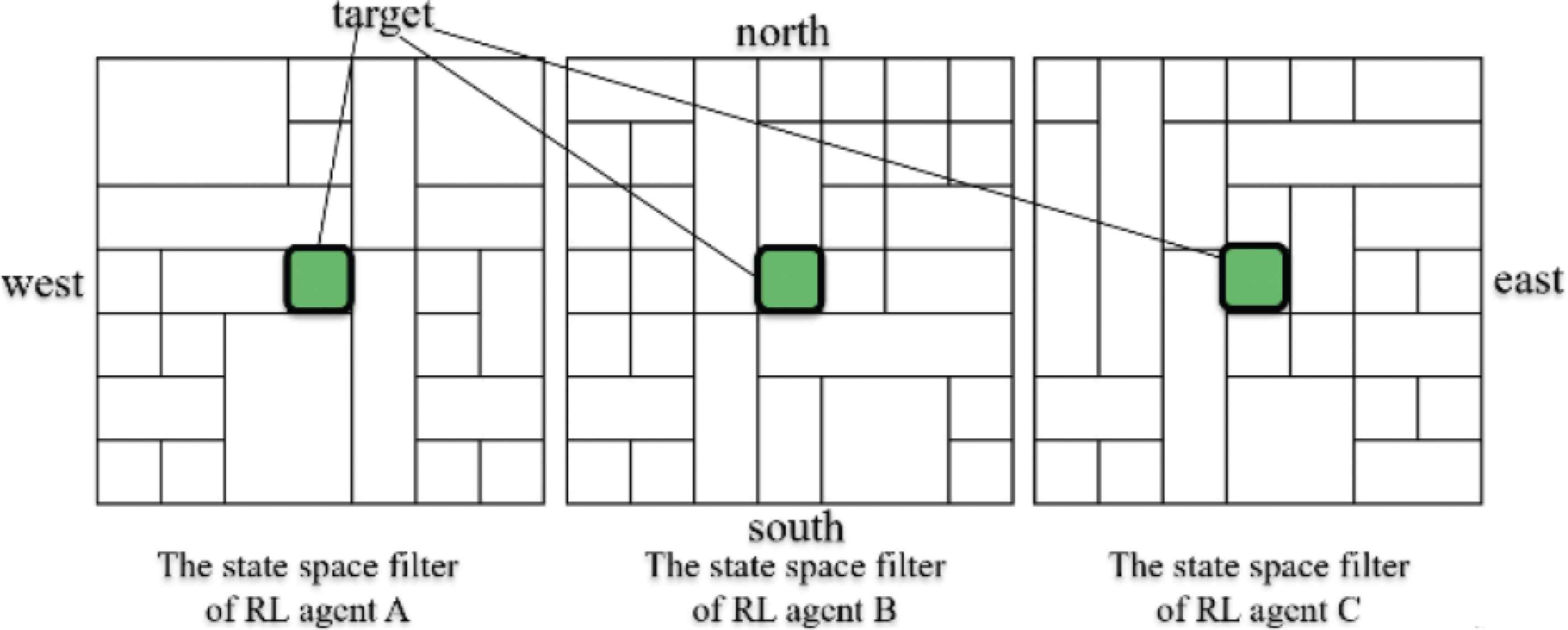
An example of obtained state space filters where wavelength λ = 50 [episode] in 1000 episode.
Thus, the effectiveness of role differentiation by introducing the fluctuation parameter into the state space filter is confirmed. We deem the effectiveness of role differentiation to be the result of “Overgeneralizing”.
6. CONCLUSION
In this paper, we introduced a “fluctuation parameter” into a state space filter in order to realize “Overgeneralizing” which is one of the “Cognitive distortions”. Through computational examples, we confirmed the effectiveness of role differentiation by introducing the fluctuation parameter into the state space filter. The effectiveness of role differentiation is deemed to be a result of “Overgeneralizing”.
Our future projects include applying the proposed method to real world problems, such as improving work allocation tables produced by head nurses. The use of this model may assist head nurses in defining rules for making work allocation tables, and taking account into the compatibility of different nurses and evolving working relationship between nurses, value-functions which are difficult to set beforehand.
CONFLICTS OF INTEREST
The authors declare they have no conflicts of interest.
ACKNOWLEDGMENT
This work was supported by JSPS KAKENHI Grant Number JP19K04906.
AUTHORS INTRODUCTION
Dr. Masato Nagayoshi
 He is an Associate Professor of Niigata College of Nursing. He graduated from Kobe University in 2002, and received Master of Engineering from Kobe University in 2004 and Doctor of Engineering from Kobe University in 2007. He is a member of IEEJ, SICE, and ISCIE.
He is an Associate Professor of Niigata College of Nursing. He graduated from Kobe University in 2002, and received Master of Engineering from Kobe University in 2004 and Doctor of Engineering from Kobe University in 2007. He is a member of IEEJ, SICE, and ISCIE.
Mr. Simon J. H. Elderton
 He is an Associate Professor of Niigata College of Nursing. He graduated from University of Auckland with an Honours Masters degree in Teaching English to Speakers of Other Languages in 2010. He is a member of JALT, Jpn. Soc. Genet. Nurs., and JACC.
He is an Associate Professor of Niigata College of Nursing. He graduated from University of Auckland with an Honours Masters degree in Teaching English to Speakers of Other Languages in 2010. He is a member of JALT, Jpn. Soc. Genet. Nurs., and JACC.
Dr. Hisashi Tamaki
 He is a Professor of Graduate School of Engineering, Kobe University. He graduated from Kyoto University in 1985, and received Master of Engineering from Kyoto University in 1987 and Doctor of Engineering from Kyoto University in 1993. He is a member of ISCIE, IEEJ, SICE, and ISIJ.
He is a Professor of Graduate School of Engineering, Kobe University. He graduated from Kyoto University in 1985, and received Master of Engineering from Kyoto University in 1987 and Doctor of Engineering from Kyoto University in 1993. He is a member of ISCIE, IEEJ, SICE, and ISIJ.
REFERENCES
Cite this article
TY - JOUR AU - Masato Nagayoshi AU - Simon J. H. Elderton AU - Hisashi Tamaki PY - 2021 DA - 2021/05/27 TI - A Multi-agent Reinforcement Learning Method for Role Differentiation Using State Space Filters with Fluctuation Parameters JO - Journal of Robotics, Networking and Artificial Life SP - 6 EP - 9 VL - 8 IS - 1 SN - 2352-6386 UR - https://doi.org/10.2991/jrnal.k.210521.002 DO - 10.2991/jrnal.k.210521.002 ID - Nagayoshi2021 ER -
