Design of a Nonlinear Generalized Predictive Controller based on Database-Driven Approach
- DOI
- 10.2991/jrnal.k.210922.015How to use a DOI?
- Keywords
- GPC; database-driven approach; nonlinear systems
- Abstract
This paper presents a Generalized Predictive Control (GPC) design scheme based on database-driven approach for nonlinear systems. In industrial systems, lots of controlled plants with unknown time-delay and strong nonlinearity, are difficult to be handled in terms of control performance. The databased-driven approach has been attracted attention to tackle non-linearity issue without system information. On the other hand, GPC is considered in cases where the time-delay is unknown. The proposed scheme is validated through a numerical simulation.
- Copyright
- © 2021 The Authors. Published by Atlantis Press International B.V.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
The tuning of controller for controlled processes is of increased attentions for industrial process. A variety of controllers are required to deal with broad range of applications to maintain the process performance. These controllers are either classical the Proportional-Integral-Derivative (PID) controller, or more advanced adaptive predictive controller. For simple processes, the conventional PID controller can achieve satisfied performance, however, it may degrade the performance in the case of some changes or uncertainties for some complex processes. Maintaining system performance becomes an essential issue in industrial processes. Unfortunately, it is typically complicated and expensive.
Predictive control is considered as an advanced control strategy since it uses a long-range prediction idea. As a result, the excellent performance can be achieved. One of popular in the family of long-range predictive controllers is the Generalized Predictive Control (GPC) algorithm [1] which adapts to process time-delay and model order based on the long-range prediction. Therefore, it is shown to be particularly effective for the self-tuning control of industrial processes [2], in which are widely applied. However, regarding to the existing GPC, the excellent control behavior can be achieved, provided that the number of parameters in the model are required. It is important to include a reasonable representation of disturbances and other unknown dynamics, such that the correct controller can be designed. In other words, the GPC is model-based technique, so good performance needs a high-quality process model. Unfortunately, as it is well known, modeling for an industrial process using first principles or identification is a difficult task. Further, even the mathematical model of the industrial process is established, it only approximates the process but not involves entire process dynamics. Moreover, it is time- and cost-consuming to build the relative accurate complicate model of industrial process. Therefore, some challenges have been addressed in the model-based technique.
The industrial processes have undergone significant changes along with the rapid development of information technology. It is possible to store and process huge amounts of process data with the help of computers. In recent years, it is a trend to design the controller by directly using online or offline Input/Output (I/O) data obtained from the controlled system or knowledge, instead of the explicit mathematical model of the controlled process [3]. Several methods [4,5] have been proposed by considering the above idea. Moreover, the data-oriented GPC controller [6] has been proposed, where the initial polynomials parameters are estimated from the I/O data, and then the polynomials are calculated based on the iterative calculation. However, the controller is operated in an offline manner, which the controller parameters are not modified during the operation. Consequently, it leads to an issue that the control performance may be degraded for some systems with strong non-linearity.
The database-driven approach [7,8] is one of control strategies applied in systems with strong non-linearity since it can tune the control parameters rapidly at each equilibrium point. Furthermore, the database-driven approach performs the tuning in on-line manner to cope with the operation condition along the time, such that the performance deterioration can be avoided. Successful implementations of the data-driven approach have been presented in the technical literatures [9–11].
Based on the above observation, this paper newly presents a nonlinear generalized predictive controller based on databased-driven approach. The main contributions lie in twofold. One is that the proposed controller can deal with time-delay involved in nonlinear systems. The other one is that the proposed controller is operated in on-line manner by exploiting the measured I/O data, which results in improving the performance.
The remainder of this paper is as follows. The Section 2 states the problem. The Section 3 gives the details of the proposed scheme. In Section 4, the numerical simulation and comparative study are conducted to verify the effectiveness, and Section 5 concludes the paper.
2. PROBLEM STATEMENT
Consider the following nonlinear system:
When considering regulation about a particular operation point, it is reasonable to assume that the nonlinear system can be described as a locally-linearized model by the following equation:
Based on the above statement, the problem to be addressed in this paper is as follows. The block diagram of proposed scheme is depicted in Figure 1. Use the batch of data, collected the historical data, to generate the initial database. Then the nonlinear predictive controller can be updated by exploiting the I/O data, and the controller generates u(t) to control the system Equation (1) based on database-driven approach aiming at tracking the reference signal w(t).
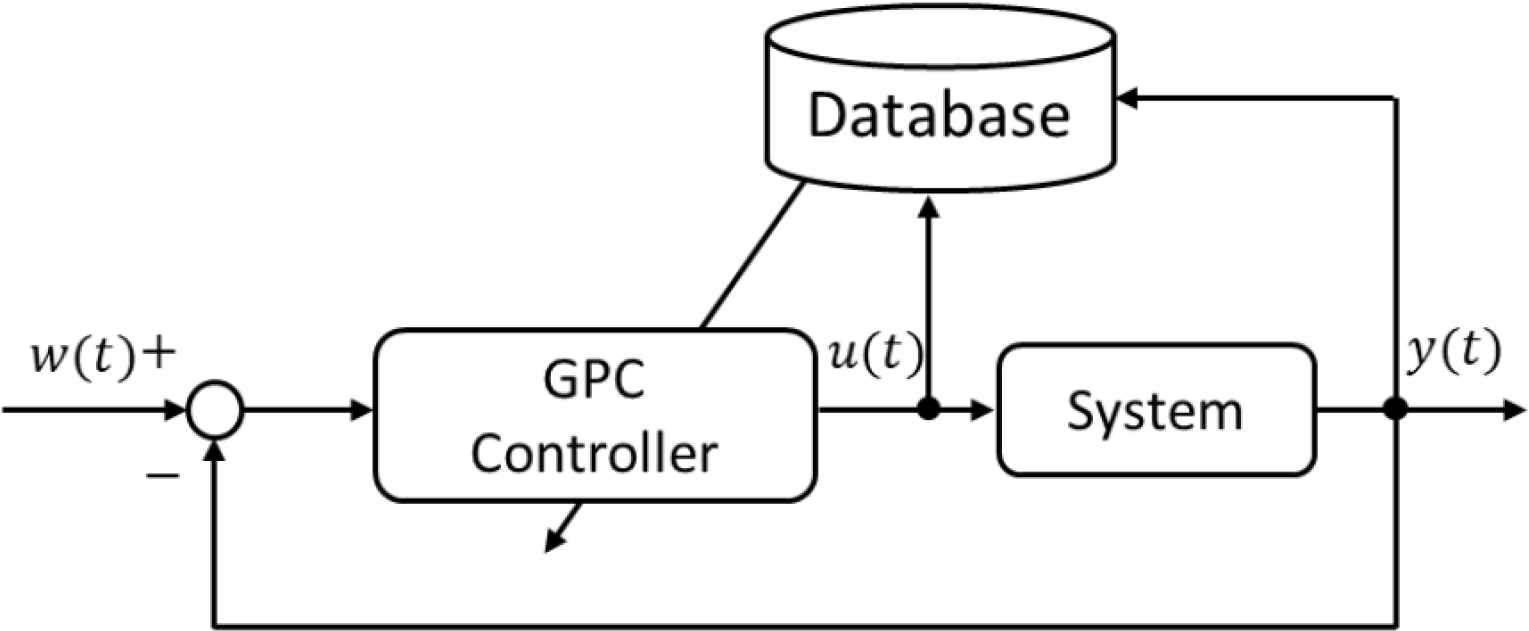
Block diagram of the proposed scheme.
3. PROPOSED SCHEME DESIGN
3.1. Generalized Predictive Control
The GPC law is derived based on the minimization of the criterion in the following equation:
To derive the j-step ahead predictive output y(t + j) based on system (3), the following Diophantine equations are introduced.
Multiplying the system (3) by Ej(z−1) and (7), and then obtain the following equation:
Consider the definition Ej(z−1) B(z−1) = Gj(z−1). And the future noise term is independent with current step. The above equation can be written as:
It can also be re-written through (7) by:
Then the above equations can be expressed in a vector form as follows.
The minimization of J by the partial derivative method with respect to ũ and obtain the control sequence.
It should be noted that the first element is the ∆u(t), then the current control u(t):
3.2. Derivation of Output by Control Parameters
Recall Equation (10) and for j = 1 to give the one-step ahead predictive output as:
Therefore, the database-driven approach is introduced to address this issue. The database-driven approach works in an on-line manner, which means the polynomials F1(z−1, t) and Gj(z−1, t) will be updated based on the database.
The following subsection will review the database-driven approach by involving the parameters F1(z−1, t) and Gj(z−1, t). The above Equation (17) is re-written in the form of information vector as:
3.3. Database-driven Approach
The detail of this approach will be reviewed in this subsection. The query
The procedure of the database-driven approach is summarized in the following.
[STEP 1] Generate the initial database
The historical data can be obtained by employing some conventional methods. The initial data set then is used to identify the polynomial parameters when j = 1, namely F1(z−1) and Gj(z−1). Then the input and output data, reference signal and F1(z−1) and Gj(z−1) are stored in the database.
[STEP 2] Calculate the distance and select the neighbors
The distance between the query and the information vector
[STEP 3] Re-calculate the initial polynomial parameters
In this step, the selected Ne-pieces neighbors’ data are used to re-calculate the parameters F1(z−1, t) and Gj(z−1, t) in an on-line manner by linearly weighted average [12] as follows:
[STEP 4] Parameters’ adjustment
The parameters obtained in the last STEP θold(t) are updated in an online manner to achieve satisfactory performance by the following steepest descent method.
4. NUMERICAL SIMULATION
In this section, we have conducted the simulation and illustrate the effectiveness of the proposed scheme. The Hammerstein model [13] is considered and is given in the following form:
The comparative study is firstly tested in the case where the polynomials F1(z−1) and Gj(z−1) at step j = 1 are the fixed value. The user-specified parameters are shown in Table 1.
| The orders of information vector | ny = 2 |
| nu = 5 | |
| Time-delay | d = 3 |
| Weighting factor | λ = 4 |
| Predictive horizon | 10 |
The user-specified parameters
The simulation results are shown in Figure 2, where shows the oscillation when the reference signal w(t) = 2. The tracking performance is suppressed in this area due to the strong nonlinearity.
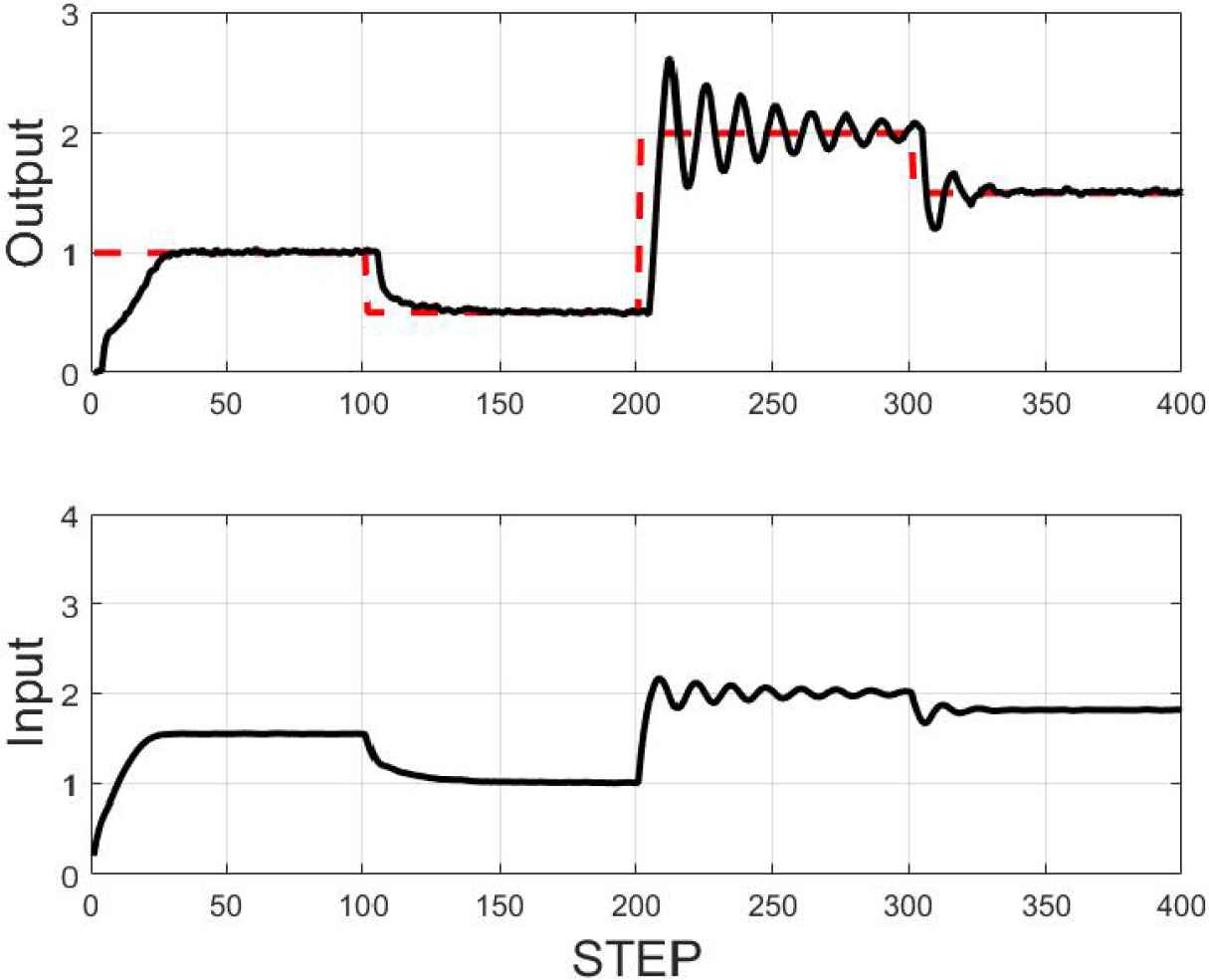
Control results using the data-oriented GPC.
The proposed scheme then is used, and the control results are shown in Figure 3. The user-specified are given in Table 2.
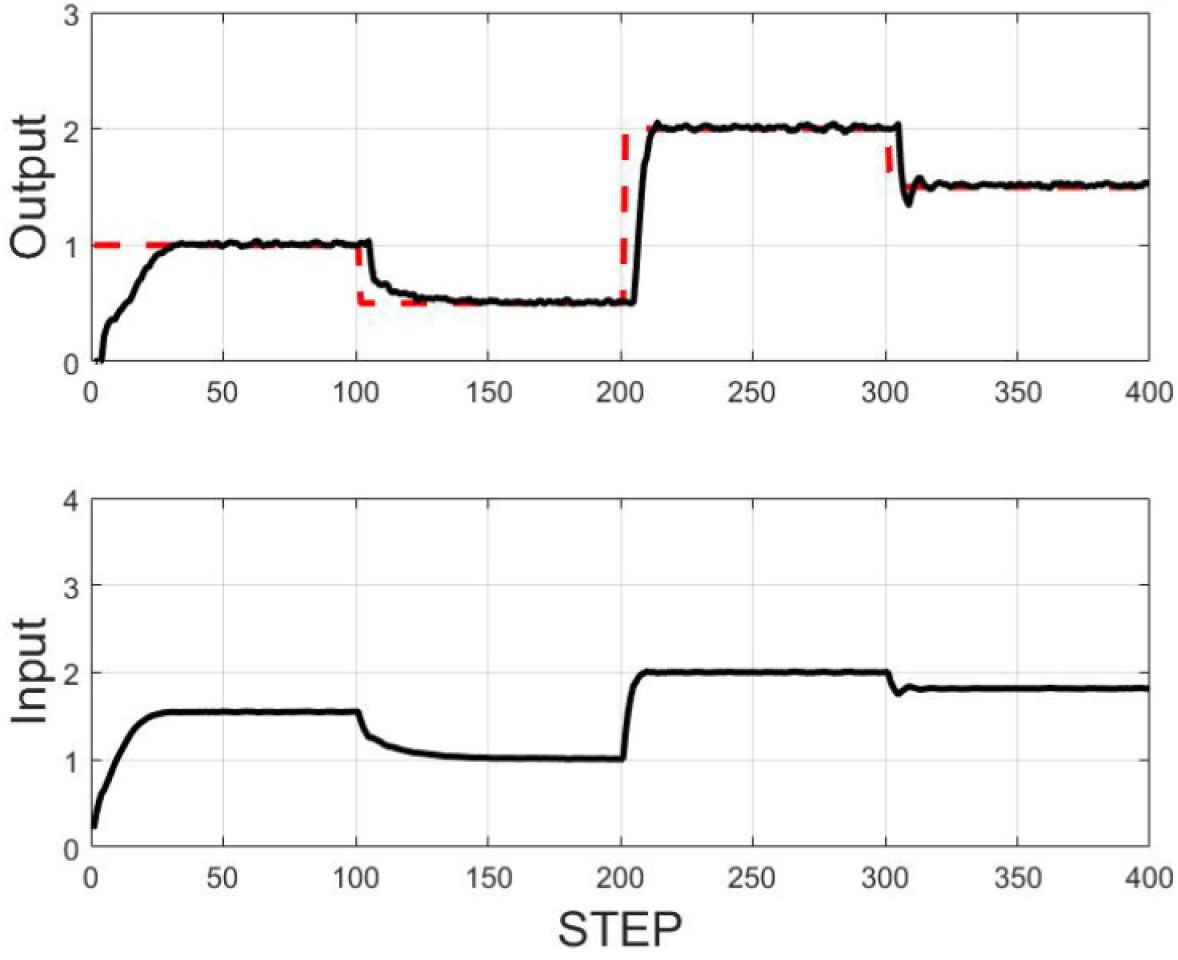
Control results using the proposed scheme.
| The orders of information vector | ny= 2 |
| nu= 5 | |
| Time-delay | d = 3 |
| Weighting factor | λ = 4 |
| Predictive horizon | 10 |
| Initial database | 150 |
| Learning rate for F1(z−1) | 0.0001 |
| Learning rate for Gj(z−1) | 0.1 |
The user-specified parameters
The control result is shown in Figure 3 where shows the stable tracking property, particularly when the reference signal w(t) = 2. The trajectories of polynomial F1(z−1, t) and Gj(z−1, t) are illustrated in Figures 4 and 5, respectively.
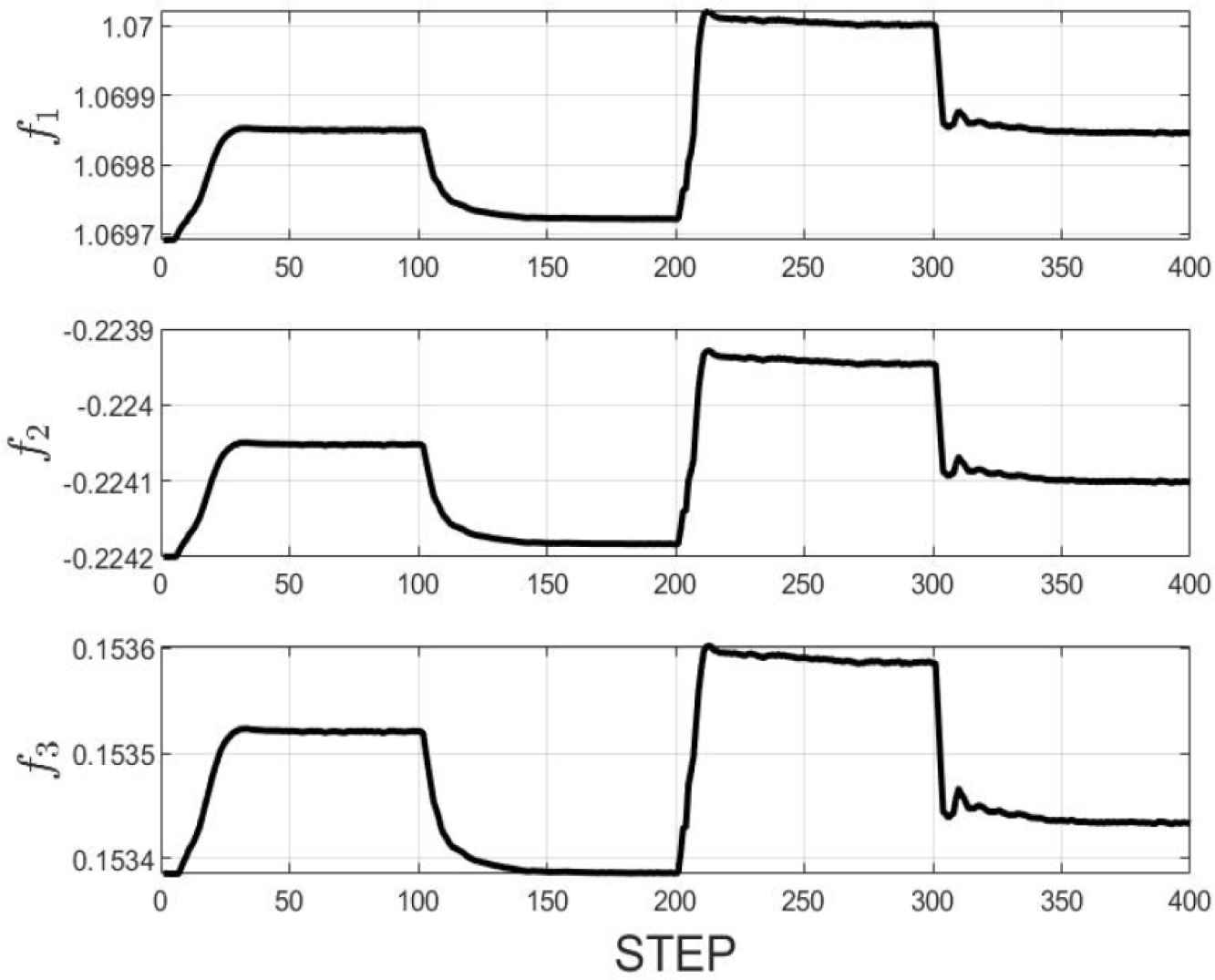
Trajectory of F1(z−1, t).
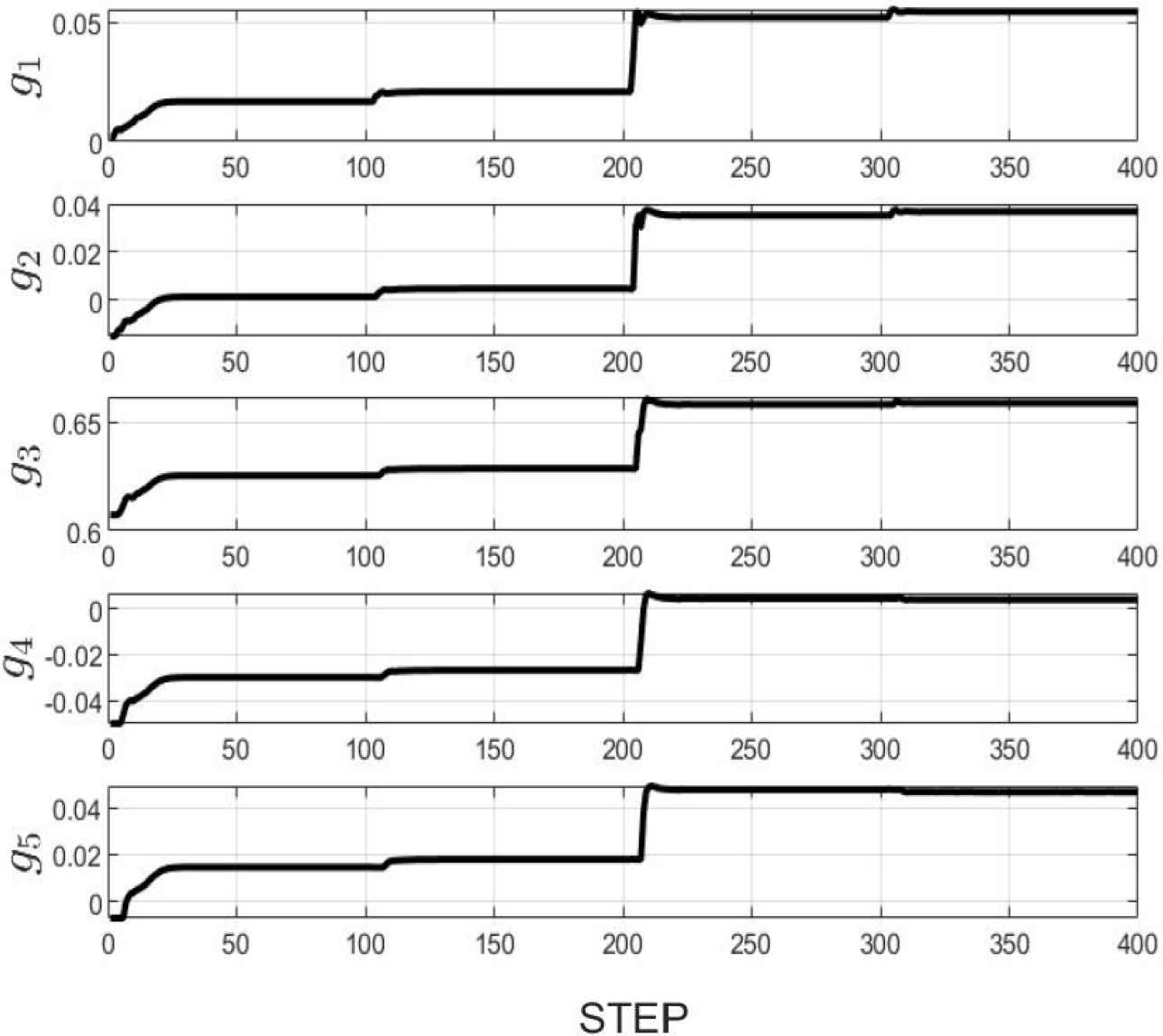
Trajectory of G1(z−1, t).
The control results from the proposed scheme outperform the ones in comparative study, which demonstrates the effectiveness of the proposed scheme.
5. CONCLUSION
In this paper, the design of a nonlinear GPC controller based on database-driven approach has been presented. First, according to the proposed scheme, the model information is not required in designing the controller. Then, the database-driven approach is considered to deal with systems with strong non-linearity and provides a way for the online utilization of the proposed scheme. Furthermore, the proposed scheme inherits the advantage of GPC algorithm such that good performance can be achieved regardless of time-delay. Finally, the effectiveness has been verified on a numerical simulation and comparative study. The experimental evaluation will be in our future work.
CONFLICTS OF INTEREST
The authors declare they have no conflicts of interest.
AUTHORS INTRODUCTION
Dr. Zhe Guan
 He received the M.S. degree and D. Eng. degree in Control System Engineering from the Hiroshima University, Japan, in 2015 and 2018, respectively. He is currently working in KOBELCO Construction Machinery Dream-Driven Co-Creation Research Center, Hiroshima University, Japan. He was a visiting postdoc with the Department of Electrical and Computer Engineering, University of Alberta from April to June in 2019. His current research interests are in area of adaptive control, data-driven control, Reinforcement Learning and their applications. He is a member of Society of Instrument and Control Engineers in Japan (SICE).
He received the M.S. degree and D. Eng. degree in Control System Engineering from the Hiroshima University, Japan, in 2015 and 2018, respectively. He is currently working in KOBELCO Construction Machinery Dream-Driven Co-Creation Research Center, Hiroshima University, Japan. He was a visiting postdoc with the Department of Electrical and Computer Engineering, University of Alberta from April to June in 2019. His current research interests are in area of adaptive control, data-driven control, Reinforcement Learning and their applications. He is a member of Society of Instrument and Control Engineers in Japan (SICE).
Prof. Toru Yamamoto
 He received the B. Eng. and M. Eng. degrees from the Tokushima University, Japan, in 1984 and 1987, respectively, and the D. Eng. degree from Osaka University, Japan, in 1994. He is currently a Professor with the Department of Smart Innovation, Graduate School of Advanced Science and Engineering, Hiroshima University, Japan, and a leader of the National Project on Regional Industry Innovation with support from the Cabinet Office, Government of Japan. He was a Visiting Researcher with the Department of Mathematical Engineering and Information Physics, University of Tokyo, Japan, in 1991, and an Overseas Research Fellow of the Japan Society for Promotion of Science (JSPS) with the Department of Chemical and Materials Engineering, University of Alberta for 6 months in 2006. His current research interests are in area of self-tuning & learning control, data-driven control, and their implementation for industrial systems. He was a National Organizing Committee Chair of 5th International Conference on Advanced Control of Industrial Processes (ADCONIP 2014) and General Chair of SICE (Society of Instrument and Control Engineers in Japan) Annual Conference 2019, both held in Hiroshima. He is a Fellow of SICE, Institute of Electrical Engineers of Japan (IEEJ) and Japan Society of Mechanical Engineers (JSME).
He received the B. Eng. and M. Eng. degrees from the Tokushima University, Japan, in 1984 and 1987, respectively, and the D. Eng. degree from Osaka University, Japan, in 1994. He is currently a Professor with the Department of Smart Innovation, Graduate School of Advanced Science and Engineering, Hiroshima University, Japan, and a leader of the National Project on Regional Industry Innovation with support from the Cabinet Office, Government of Japan. He was a Visiting Researcher with the Department of Mathematical Engineering and Information Physics, University of Tokyo, Japan, in 1991, and an Overseas Research Fellow of the Japan Society for Promotion of Science (JSPS) with the Department of Chemical and Materials Engineering, University of Alberta for 6 months in 2006. His current research interests are in area of self-tuning & learning control, data-driven control, and their implementation for industrial systems. He was a National Organizing Committee Chair of 5th International Conference on Advanced Control of Industrial Processes (ADCONIP 2014) and General Chair of SICE (Society of Instrument and Control Engineers in Japan) Annual Conference 2019, both held in Hiroshima. He is a Fellow of SICE, Institute of Electrical Engineers of Japan (IEEJ) and Japan Society of Mechanical Engineers (JSME).
REFERENCES
Cite this article
TY - JOUR AU - Zhe Guan AU - Toru Yamamoto PY - 2021 DA - 2021/10/11 TI - Design of a Nonlinear Generalized Predictive Controller based on Database-Driven Approach JO - Journal of Robotics, Networking and Artificial Life SP - 229 EP - 233 VL - 8 IS - 3 SN - 2352-6386 UR - https://doi.org/10.2991/jrnal.k.210922.015 DO - 10.2991/jrnal.k.210922.015 ID - Guan2021 ER -
