Analysis and Stability Control of a Novel 5D Hyperchaotic System
- DOI
- 10.2991/jrnal.k.211108.003How to use a DOI?
- Keywords
- Novel 5D hyperchaotic system; hyperchaos control; Lyapunov stability theory; global asymptotic stability
- Abstract
In this paper, a novel Five-Dimensional (5D) autonomous hyperchaotic system is presented, and the characteristics of the 5D system are given in brief. For stability control of the 5D hyperchaotic system, a linear feedback controller and its simplification are designed via the Lyapunov stability theory, so that the 5D system is no longer hyperchaotic but globally asymptotically converges to the equilibrium point at the origin. The numerical simulation results are given to illustrate the feasibility and effectiveness of the method.
- Copyright
- © 2021 The Author. Published by Atlantis Press International B.V.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
Hyperchaos was first proposed by Otto Rössler in 1979 [1]. Since then, many novel hyperchaotic systems have been formulated. To obtain hyperchaos, the system need to satisfy the following two important requisites. Firstly, the minimal dimension of the phase space that embeds a hyperchaotic attractor should be at least four, which requires the minimum number of coupled first-order autonomous ordinary differential equations to be four. Secondly, the number of terms in the coupled equations giving rise to instability should be at least two, of which at least one should have a nonlinear function [2]. Therefore, hyperchaos is much more complicated than chaos, and it has greater engineering significance and application prospect in signal processing, secure communication and so on.
In this paper, a novel 5D hyperchaotic system, which has been introduced in Wei and Niu [3], is reviewed. Stability control of the 5D system would be discussed, and some simulation results would be given to demonstrate the validity of the designed linear feedback controllers.
2. THE NOVEL 5D HYPERCHAOTIC SYSTEM
The dynamic equations of the novel 5D hyperchaotic system are formulated as
Let the initial values of the 5D system (1) be (x0, y0, z0, v0, w0) = (1, 1, 1, 1, 1), then the Lyapunov exponents respectively are λ1 = 0.8732 > 0, λ2 = 0.1282 > 0, λ3 = −0.0013 ≈ 0, λ4 = −0.5770 < 0 and λ5 = −8.4231 < 0. It indicates that the 5D system (1) is hyperchaotic. The attractors of the 5D hyperchaotic system (1) are shown in Figure 1.
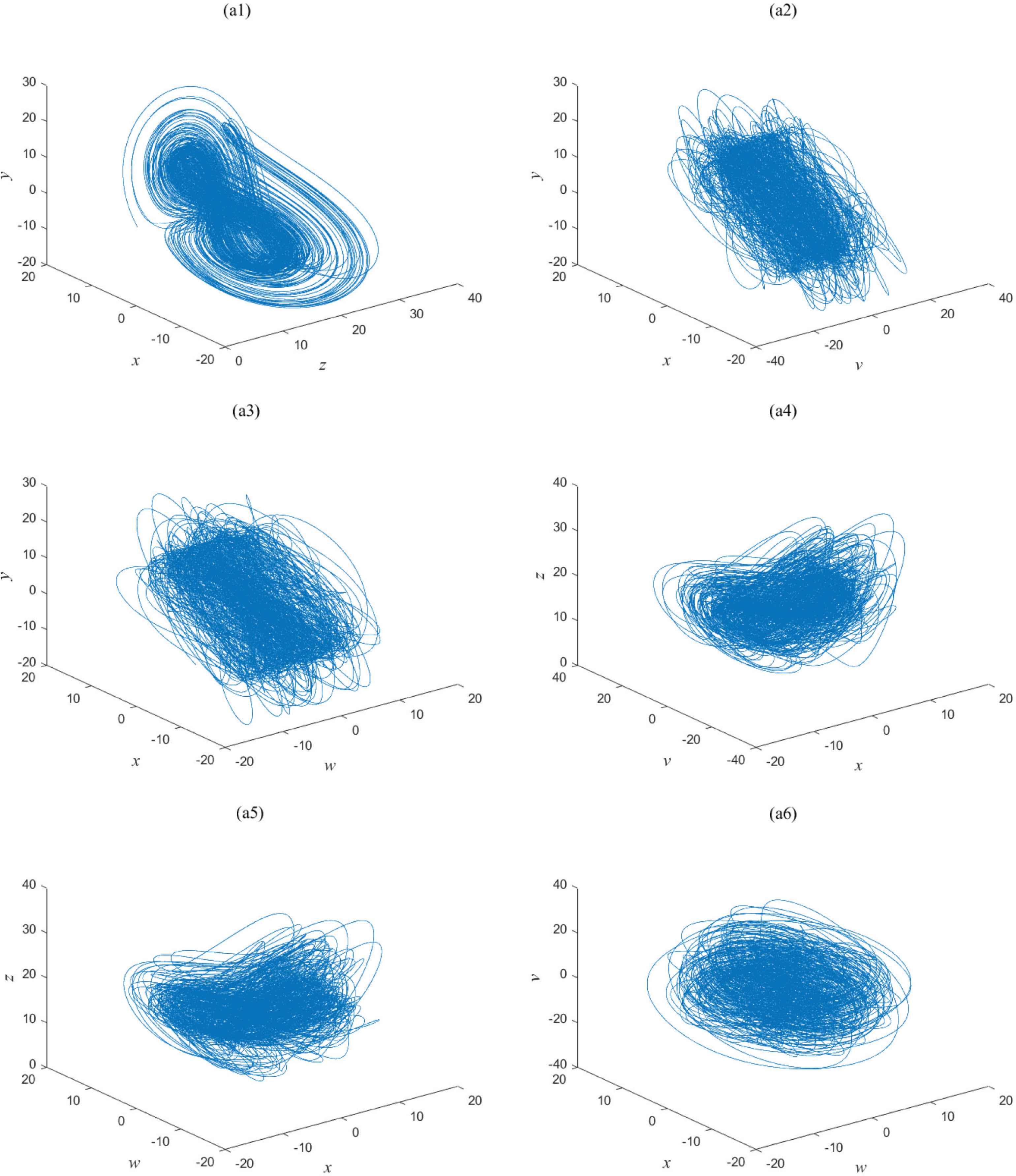
Attractors of the 5D hyperchaotic system: (a1) z-x-y; (a2) v-x-y; (a3) w-x-y; (a4) x-v-z; (a5) x-w-z; (a6) w-x-v.
3. HYPERCHAOS CONTROL OF THE 5D SYSTEM
3.1. Formulation of the Controlled System
The controlled system is represented as
3.2. Design of the Linear Feedback Controller
Theorem 1.
Let x = 0 be an equilibrium point for
then x = 0 is globally asymptotically stable [4].
From Theorem 1, take a continuously differentiable function
For
From Theorem 1, the controlled system (2) is globally asymptotically stable at the origin. Thus, the controller uc can be designed as
3.3. Numerical Simulation under the Controller uc
The curves of the state variables of the controlled system (2) before and after adding the controller uc are shown in Figures 2 and 3 respectively. Comparing Figure 3 with Figure 2, it can be found that the state variables x, y, z, v and w converge to zero asymptotically and rapidly. Meanwhile, the Lyapunov exponents of the controlled system (2) are λc1 = −1.0321, λc2 = −1.0327, λc3 = −3.0000, λc4 = −17.4666 and λc5 = −17.4687, which are all negative. It implies that the controlled system (2) is no longer hyperchaotic but asymptotically stable at the origin. It illustrates that the linear feedback controller uc is feasible and effective for hyperchaos control of the 5D system (2).
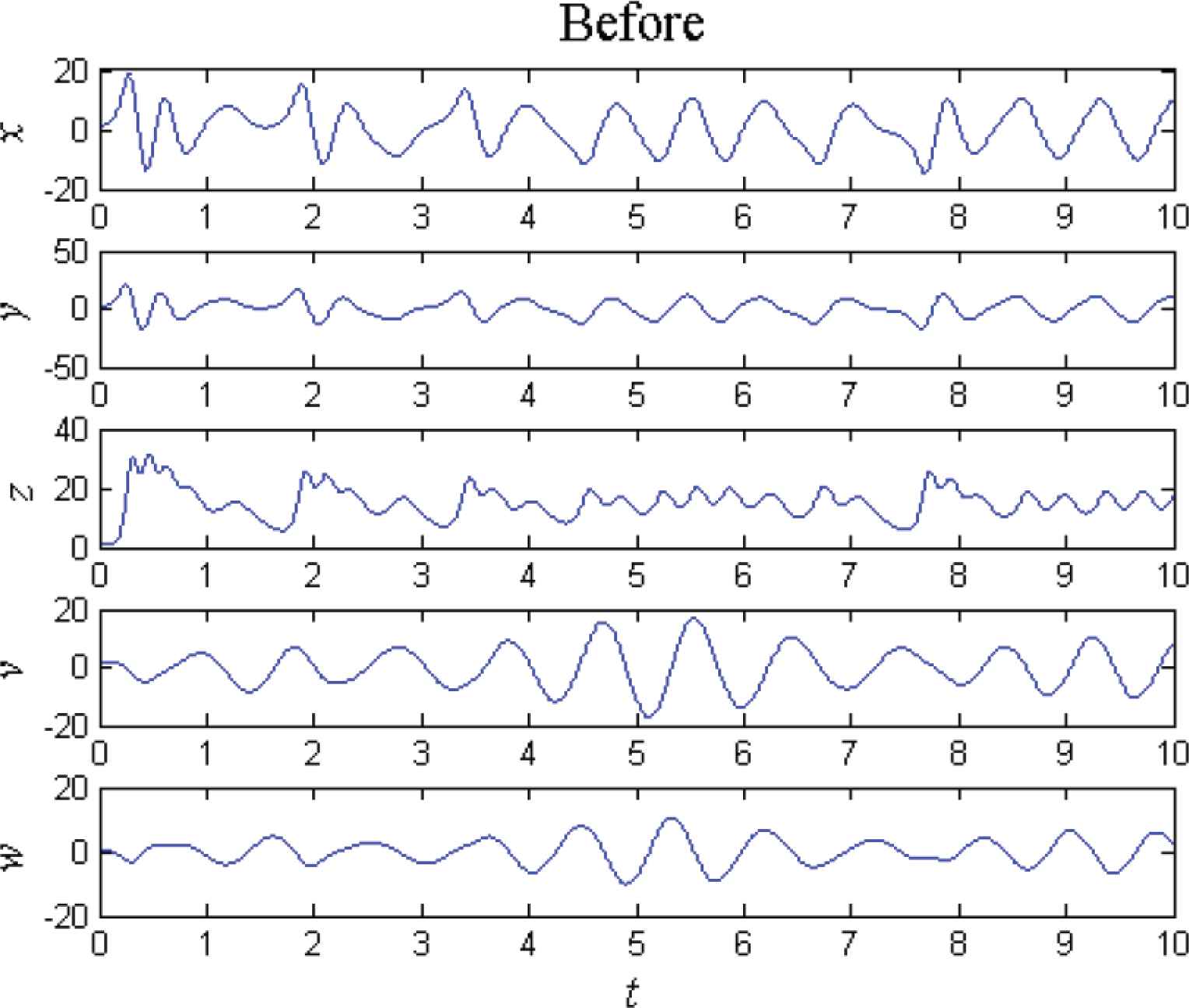
Curves of the state variables before adding uc.
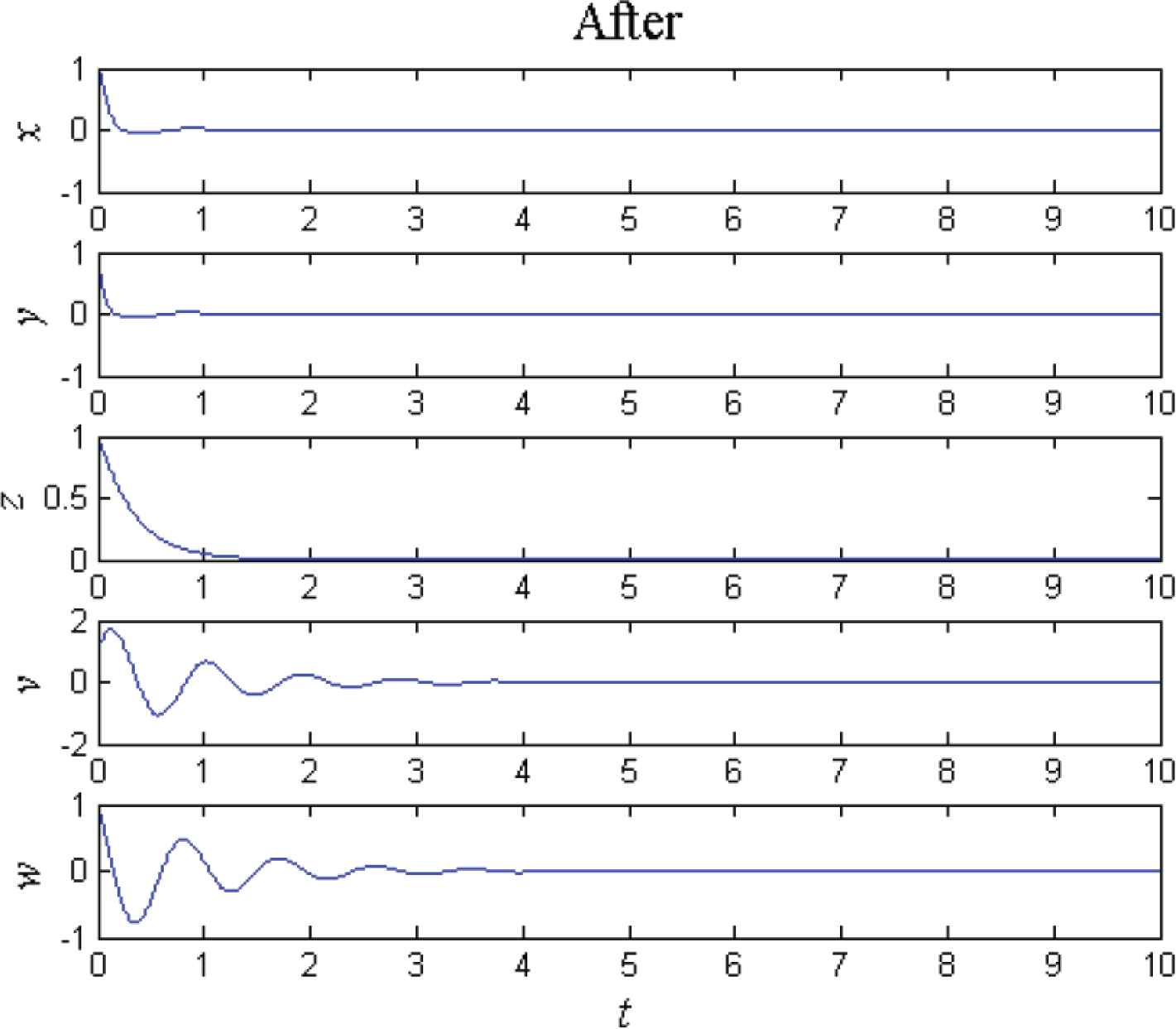
Curves of the state variables after adding uc.
3.4. Simplification of the Controller uc
Corollary 1.
Let x = 0 be an equilibrium point for
Assume that the minimum number of the feedback variables might be equal to the number of the positive Lyapunov exponents [5]. The 5D hyperchaotic system (1) has two positive Lyapunov exponents, but there are three feedback variables in Equation (5). Still take Equation (3) as a Lyapunov function candidate for the controlled system (2). Now let k4 = 0 and substitute k1 = k3 = k4 = 0 into Equation (4). Then, the derivative
For
From Corollary 1, to find
Hence, S = {x ∈ R5|x = y = z = w = 0}.
Let x(t) be a solution that belongs identically to S = {x ∈ R5|x = y = z = w = 0}, so that
Therefore, the only solution that can stay identically in
3.5. Numerical Simulation under the Simplified Controller ucs
Let the initial values still be (x0, y0, z0, v0, w0) = (1, 1, 1, 1, 1), then the curves of the state variables of the controlled system (2) before and after adding the simplified controller ucs are shown in Figures 2 and 4 respectively. Comparing Figure 4 with Figure 2, it can be found that the state variables x, y, z, v and w converge to zero asymptotically and rapidly. Meanwhile, the Lyapunov exponents of the controlled system (2) are λcs1 = −0.53246, λcs2 = −0.53248, λcs3 = −3.0000, λcs4 = −17.4664 and λcs5 = −17.4687, which are all negative. It implies that the controlled system (2) is no longer hyperchaotic but asymptotically stable at the origin. It illustrates that the simplified linear feedback controller ucs is also feasible and effective for hyperchaos control of the 5D system (2). Furthermore, the simplified controller ucs only has two feedback variables, such that it is easier to implement via circuit than the controller uc.
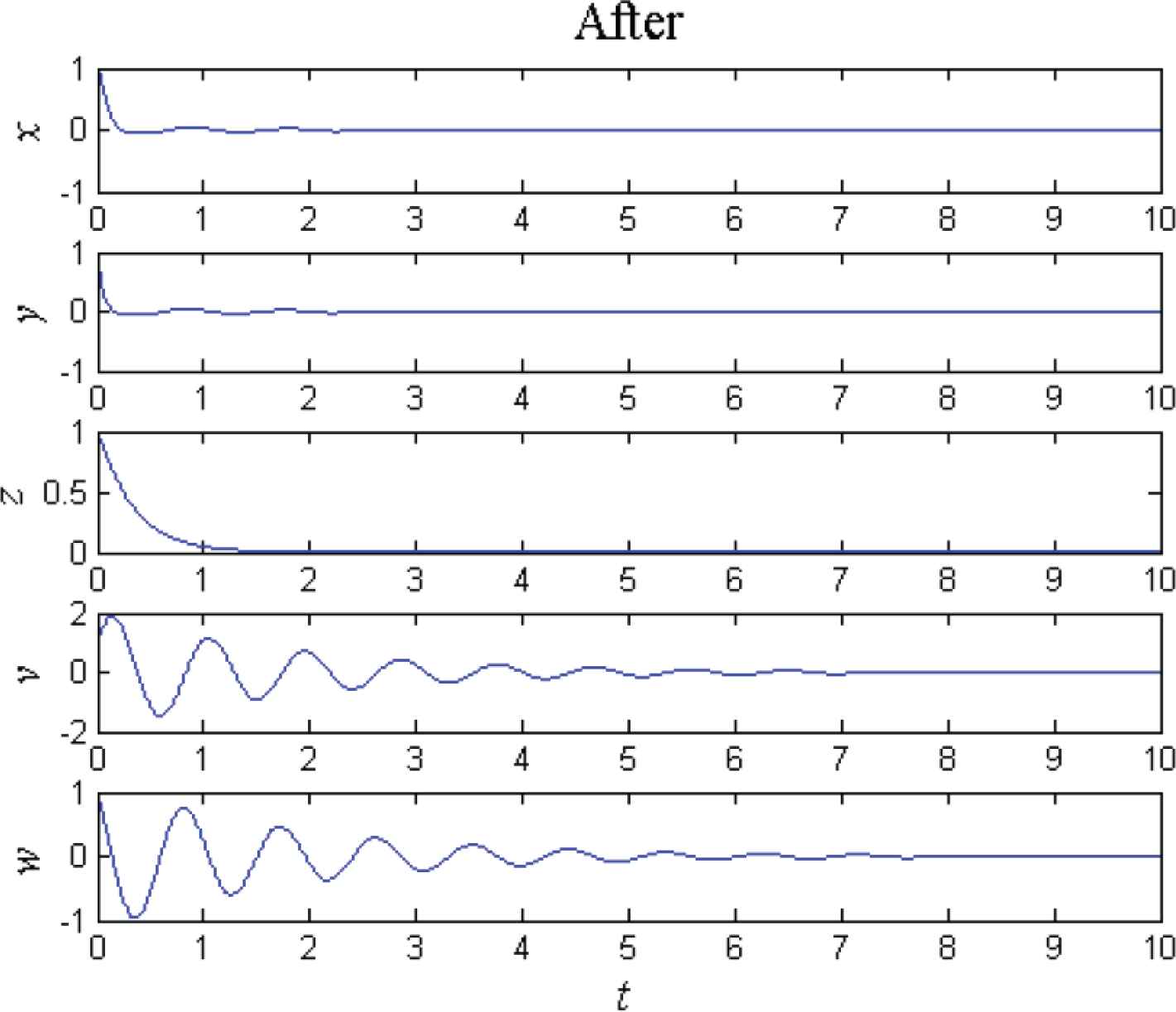
Curves of the state variables after adding ucs.
4. CONCLUSION
In this paper, a novel 5D hyperchaotic system is reviewed. For hyperchaos control of the 5D system, a linear feedback controller and its simplification are designed via the Lyapunov stability theory. The numerical simulation results demonstrate the validity of the controllers. The study in this paper has some engineering significance.
CONFLICTS OF INTEREST
The author declares no conflicts of interest.
AUTHOR INTRODUCTION
Dr. Hong Niu
 She received the PhD degree in control science and engineering from Tianjin University, China, in 2014. She is currently a lecturer with the College of Electronic Information and Automation, Tianjin University of Science & Technology, China. Her main research interests are analysis, control, synchronization and circuit implementation of chaotic and hyperchaotic systems.
She received the PhD degree in control science and engineering from Tianjin University, China, in 2014. She is currently a lecturer with the College of Electronic Information and Automation, Tianjin University of Science & Technology, China. Her main research interests are analysis, control, synchronization and circuit implementation of chaotic and hyperchaotic systems.
REFERENCES
Cite this article
TY - JOUR AU - Hong Niu PY - 2021 DA - 2021/12/27 TI - Analysis and Stability Control of a Novel 5D Hyperchaotic System JO - Journal of Robotics, Networking and Artificial Life SP - 245 EP - 248 VL - 8 IS - 4 SN - 2352-6386 UR - https://doi.org/10.2991/jrnal.k.211108.003 DO - 10.2991/jrnal.k.211108.003 ID - Niu2021 ER -
