Natural Computing Paradigm – A Concise Introduction
- DOI
- 10.2991/jrnal.2018.5.1.2How to use a DOI?
- Keywords
- Natural computing; molecular computing; self-assembly; chemical reaction computing
- Abstract
Natural computing (NC) is an emerging area of research that investigates computing techniques and models inspired by nature on one hand, and it also investigates phenomena taking place in nature in terms of computational methodologies on the other hand. Thus, research in NC congenitally has interdisciplinary flavor, which bridges between computer science and various disciplines of natural science. Because of its interdisciplinary nature, NC connects and covers a broad spectrum of fundamental research fields including biology, chemistry, physics, medical science, and so forth. In this article, we give a concise introduction to the new computing paradigm of NC. Specifically, we give an overview of selected topics of the fields from theory to experiments, where the stress is primarily put on theoretical achievements in computing paradigms called molecular computing and chemical reaction computing.
- Copyright
- Copyright © 2018, the Authors. Published by Atlantis Press.
- Open Access
- This is an open access article under the CC BY-NC license (http://creativecommons.org/licences/by-nc/4.0/).
1. Introduction
Natural computing (NC) is a novel computing paradigm inspired by nature in which NC concerns a variety of computational aspects and potential features found in natural phenomena. Also, NC has close relations to computational process inspired by those phenomena.
The goal of NC includes the following research themes. (i) From nature to information processing which means investigating computational mechanism and its implementation based on lessons from nature, and (ii) From information processing to nature which means computational analysis of nature in terms of designing new computing models and computer experiments (simulations). Further, NC also intends to exploit new applications in the fields of various disciplines involved. It is rather surprising that the conceptual source of the idea of NC has already appeared in an article of Biofizika in 1973 where an idea of cell molecular computers was discussed. Since 1974 Conrad has been conducting consistent research on the information processing capability using macro-molecules (such as proteins), and has edited a special issue in a journal entitled Molecular Computing Paradigms. His initial efforts in the early days of molecular computing have been succeeded by Head’s original work on Splicing Systems and Languages whose theoretical results on splicing phenomena should be highly appreciated, in that it was the first achievement by means of mathematical analysis on bio-chemical operations of DNA recombination. It is possible to discuss about new computing paradigms inspired by nature with a general schema of “Computing with X”, where X ranges from various sorts of materials to those of principles. Figure 1 illustrates a part of natural computing paradigms proposed so far within the “Computing with X” schema.
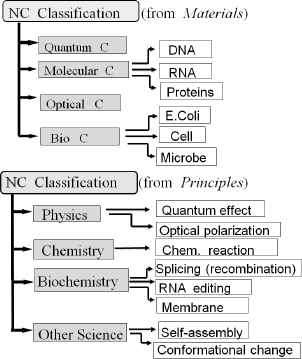
Natural Computing Paradigms Inspired by Nature (A part)
In this short article, among various computing paradigms we take up two computing paradigms “Molecular computing” (from materials), and “Chemical reaction computing” (from principles), and give an outline of fundamental results on computing capability of these new challenging ingenuity.
2. Molecular Computing Paradigm
In the early days, the goal of molecular computing seemed to replace silicon-based hardware with bio-molecular one. Unlike this intention of the early schema, however, by now it is commonly recognized that molecular computers should explore challenging applications unsuitable for existing computers.
In the theory of molecular computing, a variety of computation models have been proposed and investigated. Among others the models of computation based on self-assembly are well recognized to be of great importance in that they can provide one of the most basic frameworks for molecular computing paradigms. In fact, Adleman’s groundbreaking wet lab experiment [1] (solving a small instance of the Hamiltonian Path Problem) is a typical example of molecular computation based on the self-assembly principle.
When we make a brief revisit to the Adleman’s original work in 1994, it turns out that his algorithm may be formulated into the schema where component structures are sophisticatedly encoded into linear molecules. From these observations, a general schema of “one pot” self-assembly computation model is outlined as follows:
- 1.
design a finite set of basic units for assembly computation (one may take this finite set as a molecular program),
- 2.
put all those basic units with sufficiently high concentration into one pot, to create a random pool of a single pot (that is, leave the pot for a certain time period, resulting in producing all possible assembly of basic units),
- 3.
(if necessary) perform screening operations to extract only necessary (or unnecessary) assembly of basic units,
- 4.
detect whether or not there is an assembly with desired constraints, then answer yes if there is, and no otherwise.
Figure 2 illustrates the overview of computation schema based on self-assembly.
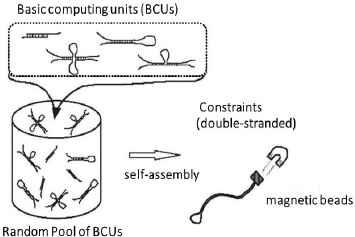
Computation Schema based on Self-assembly
In this section, we will briefly review one of the typical models based on self-assembly computation, called YAC model. Based on a unique normal form grammar G (proposed by Geffert) that can generate any recursively enumerable language, a computing model YAC has been proposed, in which an input string and every rule in G are translated(encoded) into specific forms of two-dimensional structural molecules. These basic blocks (units) of structural molecules with sticky ends are designed so that they may form a DNA complex linearly growing by self-assembly property. This means that YAC performs a simulation of computation (generation) by G, where the input string is accepted by YAC if and only if the final DNA complex forms a completely hybridized double-stranded (that is a desired constraint to be checked by screening mechanism).
It is shown that any recursively enumerable language can be recognized by YAC model. Thus, the following holds.
Proposition 1. ([2]) There effectively exists a computing model based on self-assembly principle whose computational power is Turing universal.
Other molecular computing models using high-dimensional structures have been proposed to solve NP-complete problems such as the satisfiability (SAT) problem by Jonoska et al., where 3-dimensional graph structures are used and the algorithm for SAT runs in time proportional to the number variables involved in a given formula. On the other hand, Yokomori investigated a self-assembly computing model in an abstract level, called Computing by Conformational Change (CCC), and proposes the following general schema that
(Computation)=(Self-Assembly)+(Screening Mechanism),
3. Chemical Reaction Paradigm
Inspired by the work of reaction systems (initiated by [3]), the notion of reaction automata has been introduced in [4] by extending sets in each reaction (of a reaction system) to multisets. We start this section by reviewing basic notions concerning reaction automata.
For a finite set S, a reaction in S is a 3-tuple a = (Ra, Ia, Pa) of finite multisets, such that Ra, Pa ∈ S#, Ia ⊆ S and Ra ∩ Ia =ϕ, where S# denotes the set of all finite multisets over S. The multisets Ra and Pa are called the reactant of a and the product of a, respectively, while the set Ia is called the inhibitor of a. These notations are extended to a multiset of reactions. A reaction a = (Ra, Ia, Pa) is applicable to a multiset D if Ra ⊆ D and Ia ∩ D=ϕ. As a result, D′ (=(D-Ra) ∪ Pa) is derived.
With a simple example, we introduce the notion of reaction automata. Let us consider a reaction automaton (RA) 𝒜 = (S, Σ, A, D0, f) defined as follows:
S = { p0, p1,a, b, a′, f} (symbols of objects),
Σ = {a, b} (input symbols),
A = {a0, a1, a2, a3, a4 } (reactions)}, where
a0 = ( p0, aba′, f ), a1 = ( p0a, b, p0a′ ), a2 = ( p0 a′b, ϕ, p1 ), a3 = ( p1, a′b, a, p1 ), a4 = (p1, aba′, f),
D0 = p0 (an initial multiset), and f is the final symbol.
Figure 3 illustrates an overall view of possible reaction processes in 𝒜 with inputs anbn for n ≧ 0, and we see that Lsq(𝒜) = {anbn | n ≧ 0 } which is a context-free language. We remark that this interactive process can be also performed by 𝒜 in maximally parallel manner, i.e. in the manner that every applicable reactions are performed exhaustively. That is, it holds that Lmp(𝒜)=Lsq(𝒜).
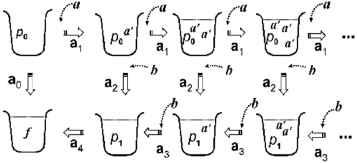
A graphic illustration of interactive processes for accepting strings in L={anbn | n ≧ 0}.
Besides both manners of applications in RAs, we often consider an extension of the sequential manner where RA allows a reaction without receiving any input symbol at each step, which is called sequential manner with λ-input mode.
We investigated the accepting powers of reaction automata with these manners of applying reactions, and obtained the following.
Proposition 2. ([4,5]) The computing power of reaction automata in maximally parallel manner coincides with that of reaction automata in sequential manner with λ-input mode. Further, both of those computing powers are Turing universal.
On the other hand, the equivalence may not hold for reaction automata in sequential manner with ordinary input mode (i.e., without the use of λ-input mode).
Proposition 3. ([5]) There exists a recursively enumerable language which cannot be accepted by any reaction automaton in sequential manner.
In order to study the role of inhibitors of reactions in the computing power of RAs, we introduced and studied a restricted RA called Chemical Reaction Automaton (CRA) in which no inhibitor is allowed ([6]).
Further, the space complexity issues of reaction automata (RAs) have been considered. By restricting the volume (i.e., the state of an RA) used in reaction process for a successful computation, some subclasses of RAs were introduced and investigated on relations between classes of languages accepted by those subclasses of RAs and language classes in the Chomsky hierarchy.
Let f(x) be a function defined on the set of natural numbers and X in {sq, mp}. The workspace of 𝒜 for w is intuitively defined as the mini-max size of multisets (appearing in all reaction sequences) necessary for accepting w. Then, an RA 𝒜 is said to be f(n)-bounded if for any w in LX(𝒜) with n=|w|, the workspace of 𝒜 for w is bounded by f(n). Then, four classes of RA languages have been investigated.
Suppose that an RA 𝒜 is f(n)-bounded. If a function f(n) is a constant k (linear, exponential), then 𝒜 is termed constant-(resp. linear-, exponential-) bounded. The class of languages accepted by constant-bounded RAs (linear-bounded RAs, exponential-bounded RAs, RAs, CRAs) in X manner is denoted by 𝒞oℛ𝒜X (resp., ℒℛ𝒜X, ℰℛ𝒜X, ℛ𝒜X, 𝒞ℛ𝒜X). The class of languages accepted by constant-bounded RAs (linear-bounded RAs, exponential-bounded RAs, RAs, CRAs) in X manner with λ-input mode is denoted by
The results on whole view of language class relations are summarized in Figure 4, where ℛℰ𝒢(𝒞ℱ, 𝒞𝒮, ℛℰ) denotes the class of regular (resp. context-free, context-sensitive, recursively enumerable) languages in Chomsky hierarchy. Further, 𝒫𝒩 denotes the class of languages generated by Petri net systems. Thus, except for the class 𝒞ℱ, each class in Chomsky hierarchy is exactly characterized by a subclass of RA languages. Further, the following result has been obtained.
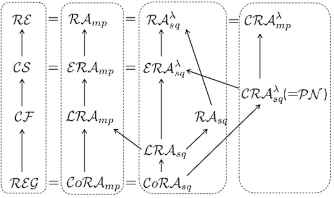
The diagram of the relations among RA language classes and Chomsky hierarchy. (A solid arrow denotes a proper inclusion.)
Proposition 4. ([6,7]) A language L is in
4. Broader Perspective
Natural computing, (NC) comprises a very broad range of computational principles that varies from well-established classical research areas to newly emerging dynamical research areas with great potentiality of many promising applications to interdisciplinary fields.
The former family may include Cellular computation, one of the oldest computing models studied since late 1940s. In Neural computation, artificial neural networks are proposed as computing systems inspired by the biological neural networks mimicking brain functions. Evolutionary computation provides a bunch of algorithms for global optimization strategy inspired by biological evolution. Further, Artificial life is a long-lasting research theme from which artificial immune algorithms have been lately developed. As for the latter family of research areas in NC, there are quite a few topics to be mentioned, while due to the space limit we can regretfully name only a part of those emergence of fascinating thoughts here: Membrane computation, Reaction-diffusion computation, Optical computation, Quantum computation, Swarm intelligence, etc.
Further, their applications to practical problems in the real world such as drug discovery in “nano-level engineering” and “medical/life science” are highly recommended to be tackled. For one example, one may refer to a medical application, lately reported, of the use of C. elegans for detecting cancer patients.
Finally, the reader interested in more details about topics discussed here and other many subjects in NC is cordially advised to consult reference papers or appropriate bibliographic sources (such as [8,9,10]).
Acknowledgements
The work partly supported by Partly supported by JSPS KAKENHI, Grant-in-Aid for Scientific Research (C) 17K00021 of The Ministry of Education, Culture, Sports, Science, and Technology, Japan, and by Waseda University grant for Special Research Project: 2017K-121.
References
Cite this article
TY - JOUR AU - Takashi Yokomori PY - 2018 DA - 2018/06/30 TI - Natural Computing Paradigm • A Concise Introduction JO - Journal of Robotics, Networking and Artificial Life SP - 6 EP - 9 VL - 5 IS - 1 SN - 2352-6386 UR - https://doi.org/10.2991/jrnal.2018.5.1.2 DO - 10.2991/jrnal.2018.5.1.2 ID - Yokomori2018 ER -
