Journal of Robotics, Networking and Artificial Life

<Previous Article In Issue
Download article (PDF)
Next Article In Issue>
Volume 5, Issue 2, September 2018, Pages 139 - 143

Reinforced Quantum-behaved Particle Swarm Optimization Based Neural Networks for Image Inspection

Authors
Li-Chun Lailclai@mail.nptu.edu.tw
Computer and Intelligent Robot Program for Bachelor Degree, National Pingtung University
Chia-Nan Kot105@nkut.edu.tw
Department of Automation Engineering, Nan Kai University of Technology
Available Online 30 September 2018.
DOI
10.2991/jrnal.2018.5.2.15How to use a DOI?
Keywords
Quantum-behaved particle swarm optimization; Niche particle; Support vector regression; Image inspection
Abstract

This paper combines the niche particle concept and quantum-behaved particle swarm optimization (QPSO) method with chaotic mutation to train neural networks for image inspection. When exploring the methodology of reinforced quantum-behaved particle swarm (RQPSO) to train neural networks (RQPSONNs) for image inspection, first, image clustering is adopted to capture feasible information. In this research, the use of support vector regression (SVR) method determines the initial architecture of the neural networks. After initialization, the neural network architecture can be optimized by RQPSO. Then the optimal neural networks can perform image inspection. In this paper, the program of RQPSONNs for image inspection will be built. The values of root mean square error (RMSE) and peak signal to noise ratio (PSNR) are calculated to evaluate the efficiency of the RQPSONNs. Moreover, the experiment results will verify the usability of the proposed RQPSONNs for inspecting image. This research can be used in industrial automation to improve product quality and production efficiency.

Copyright
Copyright © 2018, the Authors. Published by Atlantis Press.
Open Access
This is an open access article under the CC BY-NC license (http://creativecommons.org/licences/by-nc/4.0/).

1. Introduction

The application of image inspection is quite extensive including medical science, machine vision, and predicting analysis of patterns in smart automation production fields.1–5 The input images are first filtered by a high-pass filter, which is used to remove direct current and enhance high-frequency components. And then the filtered input images, which are overlapped rather than displaced from each other in the plane, serve as the input images.6 Neural networks have the capacities of learning, adaption, and nonlinear mapping of images.7

The PSO algorithm possesses the ability of high convergent speed, easily falling in some local optima is its fatal defect. Many researchers have presented revised PSO algorithms and obtained good results.8,9 Another improvement on traditional PSO algorithm is quantum-behaved particle swarm optimization (QPSO).10 However, in QPSO, particles fall into local optimal state in multimode optimization problems and cannot find any better state.11–13 To overcome the premature phenomenon in QPSO, a modified quantum-behaved particle swarm optimization (MQPSO) is proposed to identify nonlinear systems.14 Authors proposed niche particle swarm optimization (NPSO) for image segmentation.15 In NPSO algorithms, particles changing the place of the course to center the appropriate position (niche) of the particle will be absorbed. Then, particles amalgamate the small appropriate position (small niche) to become a large appropriate position (big niche).16

This paper combines the niche particle concept, quantum-behaved particle swarm optimization (QPSO) method with chaotic mutation to train neural networks for image inspection. Some experiment results verified the usability of the proposed RQPSONNs for inspecting image.

2. Modified Quantum Particle Swarm Optimization

From the view of classical dynamics, to avoid explosion and guarantee convergence, particles must be bounded and fly in an attractive potential field. Clerc and Kennedy8 have proved that if these coefficients are properly defined, the particle’s position pi will converge to the center of potential field, pfc=[pf1c,pf2c,…,pfnc] , and is defined as:

pfic=(c1⋅r1⋅pil+c2⋅r2⋅pg)(c1⋅r1+c2⋅r2),i=1,2,…,n.
where pil and pg are the best position of the ith particle and the global best position; c1 and c2 are cognitive and social constriction coefficients, respectively; r1 and r2 are random numbers between 0 and 1.

Inspired by the behavior that particles move in a bounded state and preserve the global search ability, Sun et al.13 proposed the QPSO algorithm. In the QPSO model, the solution of time-independent Schrödinger equation for this system in one dimensional space can be expressed as:11

pi=pfic±L2⋅ln(1λ),
where λ is a random number uniformly distributed on [0, 1] and L is the characteristic length of delta potential well (called "Creativity" of particles) which specifies the search scope of a particle. The mainstream thought point and can be expressed as the following forms:13
mbest=[∑i=1npi,1n,∑i=1npi,2n,…,∑i=1npi,nn],   i=1,2,…,n,
L=2⋅β|mbest−pi|,
The creative coefficient β with adaptive annealing learning mechanism according to the change rate of optimal estimation has the form:
β=βmax−Δβ⋅(Δfit)γ,
Δfit=|pg−pil|,
where Δβ is step length of β, Δfit is the change rate of optimal estimation so far. The mechanism of adaptive annealing learning can overcome the stagnation problem to accelerate the convergent speed.

3. Reinforced Quantum-Behaved Particle Swarm Optimization Neural Networks

3.1. Radial basis function neural networks

One can use a neural network to estimate the input–output relation of a dynamic system. In this paper, radial basis function neural networks (RBFNNs) are adopted because they have a simple structure, as shown in Figure 1. When the Gaussian function is chosen as the radial basis function, RBFNNs can be expressed in the form

y^j(t+1)=∑i=1LGiwij=∑i=1Lwijexp(−‖x^−mi‖22σi2)
where x^(t)=[x^1(t),x^2(t),…,x^m(t)]T is the input vector; ŷ(t) = [ŷ1(t), ŷ2(t), …, ŷm(t)]T is the output vector; wij is the synaptic weight; Gi is the Gaussian function; mi and σi is are the center and width of Gi respectively; and L is the number of the Gaussian functions, which is also equal to the number of hidden layer nodes.

Fig. 1.

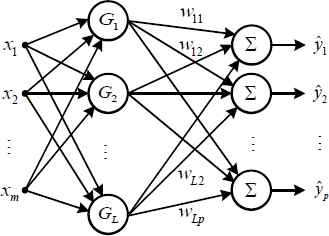
The structure of RBFNNs.

Given a set of training input–output pairs (x(k), y(k)), k = 1,2, …, N, the optimization problem of RBFNNs is to determine the values of wij, mi, and σi to minimize the index

J=∑k=1N‖y(k)−y^(k)‖2,
where ŷ(k) is the corresponding output of RBFNNs when the input x^ to the network is equal to x(k)

3.2. Niche evolution

The appropriate position evolves (niche evolution) can solve the multimodal function optimization problems effectively.17 Adopt the structure of appropriate position and search some local extreme values synchronously and avoid early convergence. It is difficult to determine the appropriate radius (niche radius) σshare. Define the niche radius as follows:18

σshare=σ0re(−λdavgR)
r=max1≤i≤N{|ui−vi|}
davg=2N(N−1)∑i=1N−1∑j=i+1Nd(φi,φj)
R=∑i=1N(ui−vi)2
where λ is an adjusting parameter, R is norm of [u, v], σ0 is the relative parameter of σshare. davg is the average distance of particles.

3.3. Chaotic mutation

The Chaos phenomenon in nonlinear science means a kind of definite but unpredictable motion state. It has already been applied to optimizing stochastic optimization problems efficiently. This study adopts chaotic mutation operation to avoid falling into some local extreme value. The logistic equation of Chaos iterating is expressed as follows:17

ηjk+1=μηjk(1−ηjk)      k=1,2,…

4. Simulation Results

In this paper, a work piece for image inspection is performed by the proposed RQPSONNs shown as Figure 2.

Fig. 2.

work piece on the conveyer belt for inspection.

The frame of image recognition is illustrated as Figure 3. Then, the experiment results of cracked work piece and perfect work piece are shown as Figures 4 and 5. Meanwhile, the values of PSNR and RMSE are shown in Table 1. The experiment results verified the usability of the proposed RQPSONNs for inspecting image.

Fig. 3.

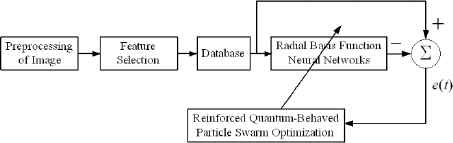
Frame of image inspection.

Fig. 4.

Cracked work piece.

Fig. 5.

Perfect work piece.

work piece PSNR RMSE
cracked work piece 18.216 13.127
perfect work piece 20.136 15.037
Table 1.

The values of PSNR and RMSE for cracked work piece and perfect work piece.

5. Conclusions

In the study, RQPSONNs combining the niche particle concept, quantum-behaved particle swarm optimization (QPSO) method with chaotic mutation to train neural networks is proposed to solve image inspection. Moreover, the experiment results have verified the usability of the proposed RQPSONNs for inspecting image.

Acknowledgements

This work was supported in part by the Ministry of Science and Technology, R.O.C., under grants MOST 106-2221-E-252-001.

References

1.LM Chen, Z Chen, and AS Feng, Image analysis algorithm and verification for on-line molecular sieve size and shape inspection, Advanced Powder Technology, Vol. 25, No. 2, 2014, pp. 508-513. https://doi.org/10.1016/j.apt.2013.08.004
2.GB Massoud, RR Denis, and D Carl, Multivariate image analysis for inspection of multilayer films, Polymer Testing, Vol. 40, 2014, pp. 196-206. https://doi.org/10.1016/j.polymertesting.2014.09.011
3.JH Chen, MC Su, R Cao, SC Hsu, and JC Lu, A self organizing map optimization based image recognition and processing model for bridge crack inspection, Automation in Construction, Vol. 73, 2017, pp. 58-66. https://doi.org/10.1016/j.autcon.2016.08.033
4.J Liu, Z Tang, W Gui, W Liu, P Xu, and J Zhu, Application of statistical modeling of image spatial structures to automated visual inspection of product quality, Journal of Process Control, Vol. 44, 2016, pp. 23-40. https://doi.org/10.1016/j.jprocont.2016.04.014
5.YG Cen, RZ Zhao, LH Cen, LH Cui, ZJ Miao, and Z Wei, Defect inspection for TFT-LCD images based on the low-rank matrix reconstruction, Neurocomputing, Vol. 149, No. Part C, 2015, pp. 1206-1215. https://doi.org/10.1016/j.neucom.2014.09.007
6.XP Deng and DM Zhao, High-pass filtering and frequency spectrum correlation for larger size image recoginition, Optik, Vol. 123, 2012, pp. 924-927.
7.P Banumathi, Artificial neural network techniques used for identifying defects in woven fabric images, International Journal of Latest Trends in Engineering and Technology, Vol. 3, No. 3, 2014, pp. 248-252.
8.A Ratnaweera, SK Halgamuge, and HC Watson, Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients, IEEE Transactions on Evolutionary Computation, Vol. 8, 2004, pp. 240-255.
9.DS Wang, DP Tan, and L Liu, Particle swarm optimization algorithm: an overview, Soft Computing, Vol. 22, No. 2, 2018, pp. 387-408. https://doi.org/10.1007/s00500-016-2474-6
10.M Clerc and J Kennedy, The particle swarm: explosion, stability, and convergence in a multidimensional complex space, IEEE Transactions on Evolutionary Computation, Vol. 1, 2002, pp. 68-73.
11.Y Fang, YD Zhao, M Ke, X Zhao, HH Iu, and KP Wong, Quantum-inspired particle swarm optimization for power system operations considering wind power uncertainty and carbon tax in australia, IEEE Transactions on Industrial Informatics, Vol. 8, No. 4, 2012, pp. 880-888.
12.SL Ho, SY Yang, GZ Ni, and J Huang, A quantum-based particle swarm optimization algorithm applied to inverse problems, IEEE Transactions on Magnetics, Vol. 49, No. 5, 2013, pp. 2069-2072.
13.J Sun, W Fang, X Wu, V Palade, and W Xu, Quantum-behaved particle swarm optimization: analysis of individual particle behavior and parameter selection, Evolutionary Computation, Vol. 20, No. 3, 2012, pp. 349-393.
14.CN Ko, YM Jau, and JT Jeng, Parameter estimation of chaotic dynamical systems using quantum-behaved particle swarm optimization bsed on hybrid evolution, Journal of Information Science and Engineering, Vol. 31, No. 2, 2015, pp. 675-689.
15.MM Bai, H Sun, and LY Wu, Method for image segmentation based on niche particle swarm optimization, Computer Engineering and Applications, Vol. 46, No. 3, 2010, pp. 183-185.
16.GJ Cheng, Y An, Z Wang, and K Zhu, Oil well placement optimization using niche particle swarm optimization, in Proceedings of 2012 Eighth International Conference on Computational Intelligence and Security (2012), pp. 61-64. (CIS),
17.H Li, Y Zhang, and A Wang, Medical image registration based on JS measure and niche chaotic mutation quantum-behaved particle swarm optimization, in Proceedings of 2010 6th International Conference on Wireless Communications Networking and Mobile Computing (2010), pp. 23-25.
18.OL Zhao, The research of the niche particle swarm optimization based on self-adaptive radius technology, in Proceeding of 2009 Asia Pacific Conference on Information Processing (2009), pp. 97-100.
<Previous Article In Issue
Download article (PDF)
Next Article In Issue>
Journal
Journal of Robotics, Networking and Artificial Life
Volume-Issue
5 - 2
Pages
139 - 143
Publication Date
2018/09/30
ISSN (Online)
2352-6386
ISSN (Print)
2405-9021
DOI
10.2991/jrnal.2018.5.2.15How to use a DOI?
Copyright
Copyright © 2018, the Authors. Published by Atlantis Press.
Open Access
This is an open access article under the CC BY-NC license (http://creativecommons.org/licences/by-nc/4.0/).

Cite this article

risenwbib
TY  - JOUR
AU  - Li-Chun Lai
AU  - Chia-Nan Ko
PY  - 2018
DA  - 2018/09/30
TI  - Reinforced Quantum-behaved Particle Swarm Optimization Based Neural Networks for Image Inspection
JO  - Journal of Robotics, Networking and Artificial Life
SP  - 139
EP  - 143
VL  - 5
IS  - 2
SN  - 2352-6386
UR  - https://doi.org/10.2991/jrnal.2018.5.2.15
DO  - 10.2991/jrnal.2018.5.2.15
ID  - Lai2018
ER  -