Quantum Clustering Ensemble
- DOI
- 10.2991/ijcis.d.201119.001How to use a DOI?
- Keywords
- Clustering ensemble; Quantum clustering ensemble; Base clustering
- Abstract
Clustering ensemble combines several base clustering results into a definitive clustering solution which has better robustness, accuracy, and stability, and it can also be used in knowledge reuse, distributed computing, and privacy preservation. In this paper, we propose a novel quantum clustering ensemble (QCE) technique derived from quantum mechanics. The idea is that basic labels are associated with a vector in Hilbert space, and a scale-space probability function can be constructed for clustering ensemble. In detail, an operator in Hilbert space is represented by the Schrodinger equation of the probability function as a solution. Firstly, the base clustering results are regarded as new features of the original dataset, and they can be transformed into Hilbert space as vectors. Secondly, a QCE model is designed and the corresponding objective function is illustrated in detail. Furthermore, the objective function is inferred and optimized to obtain the minimum result, which is then used to determine the centers. At last, 5 base clustering algorithms and 5 clustering ensemble algorithms are tested on 12 several datasets for comparing experiments, and the experimental results show that the QCE is very competitive and outperforms the state of the art algorithms.
- Copyright
- © 2021 The Authors. Published by Atlantis Press B.V.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
Ensemble learning can improve the performance of a single learning algorithm. And as a kind of unsupervised learning, unsupervised ensemble learning has a really considerable future. Cluster ensemble is a typical research direction among unsupervised learning, and it combines multiple results of base clusterings into a single consolidated clustering result. Commonly, it does not accept original data or algorithms that determined the initial results. Therefore, cluster ensemble can process the problems of knowledge reuse, privacy preservation, and distributed computing. Moreover, in the original article [1], it is viewed as a discovery of a median partition with respect to the given partitions thus it is proven to be a NP-complete problem [2,3].
The original motivation of cluster ensemble is to improve the robustness [4], accuracy, and stability [1], while a single learning algorithm has data selectivity, data adaptability, and data initialization. In most cases, the integration of multiple algorithms is more protective than a single algorithm, with better performance and higher accuracy. The other two motivations of distributed computing and knowledge reuse are discovered during the further research.
In cluster ensemble, distributed computing can be used for producing the base clustering results, and each base clustering algorithm can work independently and parallel, and then cluster ensemble just transfer all the labels of original data to a central location for aggregation. However, the cases of privacy preservation and knowledge reuse [1] are related to each other, and the reason is that the original dataset does not need to be accessed and base cluster labels are only used for cluster ensemble. In this case privacy preservation and knowledge reuse are reached. Moreover, we all know that there are some problems that causing the missing data or noise data, and when the case happens, cluster ensemble can be a choice for data analysis.
In the age of big data, privacy preserving and distributed computing are very important for governments, companies and personal users. For example, governments want to know the clusters of users, and companies just transfer the clusters or labels of users to the governments. Then, governments only recluster these results and can obtain the statistical results. Moreover, column and row-distributed cluster ensemble can be designed for the specific scenarios.
After the extensive literature surveys, it is found that quantum mechanics is not used in clustering ensemble, and the objective of cluster ensemble can be transformed into a quadratic function whose center lies among base clusterings results, furthermore, the quadratic function is known as the harmonic potential in quantum mechanics and the experimental results and a statistical test [5–8] shows the superiority of the proposed approach. Then, a quantum cluster ensemble model is proposed and the contributions of this paper are as follows:
It is the first time to apply quantum mechanism for cluster ensemble on the basis of extensive literature research, and it is also the motivation of this paper that quantum mechanism is tried to solve cluster ensemble problem.
Based on the idea of quantum, a quantum clustering ensemble (QCE) objective function is designed and the corresponding inference is illustrated in detail.
According to the inference of objective function, the corresponding algorithm is designed and stated step by step, furthermore, the extensive experiments are conducted to test the performance of the proposed model and a statistical test is conducted to ensure the superiority of the proposed approach.
The rest of this paper is organized as follows: Section 2 presents related work on cluster ensemble. Section 3 proposes QCE model. The experimental results are reported in Section 4, and then the paper concludes in Section 5 with some remarks and the future work.
2. OVERVIEW OF RELATED WORK
In this section, we present a brief overview of cluster ensemble models or algorithms. Besides, we will discuss three main categories of algorithms such as, graph-based, matrix-based and probabilistic models in detail, and other models are also introduced.
2.1. Graph-Based Models
In the original paper [1], cluster ensemble problem is transformed into a hypergraph, then a graph cut algorithm is applied to obtain the clustering ensemble result. Firstly, cluster-based similarity partitioning algorithm (CSPA) [1] is used to construct a graph according to the base clustering results, and the METIS algorithm [9] is applied to partition the graph to get final clusters. Secondly, hypergraph-partitioning algorithm (HGPA) [1] use hyperedges and nodes to represent each cluster and corresponding objects respectively and then minimal cut algorithm HMETIS [10] is applied for partitioning. Lastly, a meta-clustering algorithm (MCLA) [1] uses hyperedge collapsing operations to determine a soft cluster membership for each object. These three algorithms are very intuitive and interpretable, but they need large memory to run. Additionally, graph-based models [11,12] are proposed according to different ideas or theoretical methods. However, they all use graph-based ideas, thus convert the base clustering results to a hypergraph or a graph, and then utilize graph-partitioning algorithms to obtain ensemble clusters.
A bipartite graph-partitioning algorithm is proposed in [11], and it uses the base clustering to construct a bipartite graph, and then applies a reduction method to obtain the final clusters. The advantage is that the proposed graph models consider both objects and clusters of the ensemble as the vertices of the graph simultaneously. Furthermore, a weighted bipartite partitioning algorithm [12] is designed and it maps consensus partition to weighted bipartite graph partitioning, thus the method is more flexible than the original one. Liang et al.[13] propose a new algorithm for cluster ensemble to find nonlinear and separable clusters. They use a graph to represent the cluster relations, and then min-cut of graph is applied to obtain the final clusters. But in the proposed algorithm, the tag credibility of more clustering algorithms is not discussed.
Shi et al.[14] studied the relationship quality and diversity of base clusters, and they design a transfer cluster ensemble framework to obtain better final clusters, which is a good way to explore the clustering ensemble and transfer learning. The framework has achieved better clustering performance, but it also has a high-time complexity.
2.2. Probabilistic Models
In this subsection, cluster ensemble can be viewed as probabilistic models, and then cluster ensemble algorithms are designed according to corresponding probabilistic models. In fact, there are a lot of statistic properties of base clusterings results, so the models of cluster ensemble can take advantage of their properties to achieve a consensus clustering. Commonly, this kind of models views the base clustering labels as new feature of original data, and then Topchy et al.[3] think that base clustering labels follow an multinomial distribution, and a mixture model can generate the base clustering results. On the other hand, the hidden variable can be inferred to a final ensemble result. Due to the assumption that the data objects conform to a certain probability distribution in the algorithm, poor quality clustering results will be obtained when the assumption conditions do not match the real situation.
Yang and Jiang [15] used a hidden Markov model to design a hybrid meta-clustering ensemble, and they further used a bi-weighting scheme to solve the problems of model selection and parameters initialization. Thus, the proposed bi-weighting scheme can adaptively examine the partition process, so it can optimize the consensus functions, which improves the performance of cluster ensemble. However, the weakness of the algorithm are still existing in the algorithm, which is that generating input partitions is a time-consuming job when initial cluster analysis is done.
Punit et al.[16] proposed a new random projection, and cumulative agreement is used to aggregate fuzzy partitions. External and internal cluster validation indices are used to evaluate fuzzy partitions of random projections and then, the best partition in the ranked queue forms the base partition.
Yu et al.[17] investigated the problem of selecting the suitable cluster structures in the ensemble, which can be summarized to a more representative cluster structure. The cluster structure is first represented by mixture of Gaussian distributions, and then the parameters are estimated using the expectation maximization algorithm. Then, the similarity between two cluster structures is evaluated by several distribution-based distance functions. They propose a new approach called the distribution-based cluster structure ensemble (DCSE) framework based on this similarity comparison to find the most represented unified cluster structure. Since the algorithm assumes that every subset of data conforms to a Gaussian distribution, the results won’t be accurate when true data does not conform to a gaussian distribution, and as the dimension of data set increases, more parameters need to be estimated.
Li et al.[18] defined stability to quantify the stability of a sample, and two formulas is used to calculate samples stability. Then, clustering ensemble algorithm based on the samples stability are designed in detail. In practice, it is difficult to differentiate the stable or unstable samples.
2.3. Matrix-Based Models
The third category of algorithms is matrix-based models [19–22]. Their main idea is to form matrices such as consensus matrix, co-association matrix, or nonnegative matrix, and matrix operations from the base clustering result, which are then used to get the results of cluster ensemble. Therefore, several base clustering results are mapped into co-association matrix [19], where each entry denotes the strength of association between objects and clusters. Thus, a majority-voting algorithm is used to partition the co-association matrix to obtain the final clustering solution. The agreement among the results of base clustering is redefined in this paper [22] and the authors used a consensus matrix to represent and quantify the results. Matrix-based models are simple and easy to implement, but it is not suitable for large-scale data processing because storage and computation are quadratic.
Li et al. illustrated in the paper [20], that the problem of cluster ensemble can be formulated using the framework of nonnegative matrix factorization, which is the problem of factorizing a given nonnegative data matrix into two matrix factors under the constraint of the two matrices to be nonnegative matrices, in which there are fewer comparison algorithms.
Ye et al.[23] proposed a method for integrating dark knowledge and base clustering results, and then they convert them into a nonnegative matrix, finally, the matrix factorization operations are applied for cluster ensemble result. It uses more information of clusters, but there are more steps integrating into cluster ensemble.
Liu et al. put forward spectral ensemble clustering (SEC) in [24] to leverage the benefits of co-association matrix in information integration that run more efficiently. They disclose the theoretical similarity between SEC and weighted K-means clustering, which dramatically diminishes the algorithmic complexity. Furthermore, they derived a latent consensus function for SEC, which to our best knowledge is a novel technique to bridge co-association matrix- based algorithms to the algorithms with explicit global objective functions and further proving in theory that SEC has robustness, generalizability, and convergence properties. It is worth mentioning that SEC seems to be a promising big data clustering method.
Tao et al. [25] proposed a novel marginalized multiview ensemble clustering (
Huang et al. [26] proposed a large-scale spectral clustering (SC) algorithm based on sub-matrix construction and bipartite graph, and a large-scale ensemble algorithm, which can be used in big datasets. It is noteworthy that both of the proposed methods have linear time complexity and space complexity.
2.4. Other Models for Cluster Ensemble
There are several other models for cluster ensemble such as the evolutionary cluster-based oversampling ensemble framework proposed by Lim et al.[27]. They designed synthetic data generation method according to contemporary ideas, which can identify oversampling regions using clusters, and then an evolutionary algorithm is used to create the ensemble. Another ensemble technique using the evolutionary algorithm was proposed by Wang et al. [28]. The authors presented an improved chromosome coding proposing an improved genetic algorithm by improving the coding of chromosome where evolution rules are constructed to find the optimal chromosomes which then give the final ensemble clustering, but few data sets are used in the experiments.
Yu et al.[29] presented a technique to incorporate prior knowledge on the datasets into the ensemble framework. Their approach known as knowledge-based cluster ensemble (KCE) represents the prior knowledge on the data set in the form of pairwise constraints. Moreover, they adopted SC algorithm to generate a set of clustering solutions, but the data set used in the experiment was too small to exceed 400.
Yu et al.[30] proposed a concept to fuse multiple structures with main objective function to align individual labels obtained from different clustering solutions. The objective function is different from the traditional cluster ensemble approaches and it focuses on unifying the structures obtained from different data sources. Furthermore, an ensemble approach based on this framework called the probabilistic bagging-based structure ensemble approach (BSEA) has also been presented. Since the algorithm uses graph theory to find the most representative structure, its memory consumption may be large.
Yu et al.[31] presented double weighting semi-supervised ensemble clustering using selected constraint projection (DCECP) which utilizes constraint weighting and ensemble member weighting to address these limitations. DCECP adopts the random subspace method in combination with the constraint projection procedure to handle high-dimensional datasets. Then, it treats prior knowledge of experts as pairwise constraints, and allocates different subsets of pairwise constraints to different ensemble members. This method is superior to other semi-supervised clustering integration algorithms on high-dimensional data sets.
Parvin and Minaei-Bidgoli [32] put forward a fuzzy-weighted locally adaptive clustering (FWLAC) algorithm, which is proficient to handle imbalanced clustering situations. However, FWLAC algorithm is sensitivity to parameters but well tuning of its parameters can help overcome the sensitivity.
Yang and Jiang [33] proposed hybrid sampling-based clustering ensemble method by combining boosting and bagging algorithms where the base partitions are iteratively generated using a hybrid process. Then, a novel consensus function is proposed to encode the local and global cluster structure of base partitions into a single representation, and applies a single clustering algorithm to such representation to obtain the consensus partition. This single learning process results in high-quality clustering results and faster computing speeds.
Shi et al.[34] firstly designed an active density peak (ADP) algorithm, and then ADP is used for cluster ensemble, which is fast and effective, but this algorithm is only used on datasets with less than 700 data objects.
3. QCE MODEL
In this section, cluster ensemble problem is illustrated in detail. Then, the base labels are transformed in continuous data which is more detail than the original labels, and they can contain more information. At last, the base clustering results are viewed as the new features of the original dataset, so QCE model is designed for the final ensemble result.
3.1. Problem Formulation
About the definition of cluster ensemble, there are several ways to illustrated it in detail. Firstly, Strehl et al. [1] stated the problem of definition in 2002, and Wang et al. [35] extended its definition in 2011. The problem of clustering ensemble formulation can be defined as follows. Given
This step creates the base clusters and in the next step, we define an objective function based on normalized mutual information (NMI) [1] and the optimal result
This is a general situation in which all the base clustering results for the data points are centralized to perform the analysis. Moreover, there are three significant variants: missing value CEs, row-distributed, and column-distributed CEs [35]. All the traditional CEs have problems with processing discrete data.
3.2. Base Labels Transformation
In this subsection, we use several methods to transform the base labels into continuous data field. (1) The fuzzy partition achieved by soft clustering algorithms comprises the confidence and the distance to the cluster centers and can be directly used in QCE and (2) the cluster centers obtained by hard clustering algorithms can be used to represent the base labels.
In fact, base learning algorithms can attain other knowledge such as parameters, covariance, or probability of the data points. The simplest way to extract a lot of information from the training data is to learn with many different models in parallel. During the test stage, we then average the predictions of all the models or of a selected subset of good models that make dissimilar errors.
Different models can work on different parts of the training data, and averaging the results gives us knowledge that is more comprehensive. However, for a big ensemble, this might take a lot of memory and time to give the prediction, which is not desirable in a real-world situation. Moreover, a big ensemble is vastly redundant and contains very little knowledge in each parameter. Therefore, we use soft targets to solve the problem. Soft targets efficiently transfer the function while training a base learning model, but we typically use hard targets, e.g., a category vector in which an entry is either 1 or 0 while in soft targets, the memberships overlap and are rather probabilistic distributions of the categories.
The core difference between the traditional clustering ensemble formulation and the reformulation we present here is the data type, which is either discrete or real. Besides, real data can disclose the dark knowledge and more information in the base learning model. Therefore, the new objective function for the clustering ensemble can be defined as
We design clustering ensemble algorithm based on the objective function and optimize it in the clustering process.
3.3. QCE Model
In this section, we present a novel QCE technique. In QCE, we view the base clustering labels as new features of the original data, and then we transform the base labels to continuous data. The main idea is illustrated in Figure 1. Firstly, the base labels are projected, and we can see that there are two minima in this figure. Secondly, an energy function is used to model this case and the inference of the energy function is to find the two minima, which are the cluster ensemble centers.
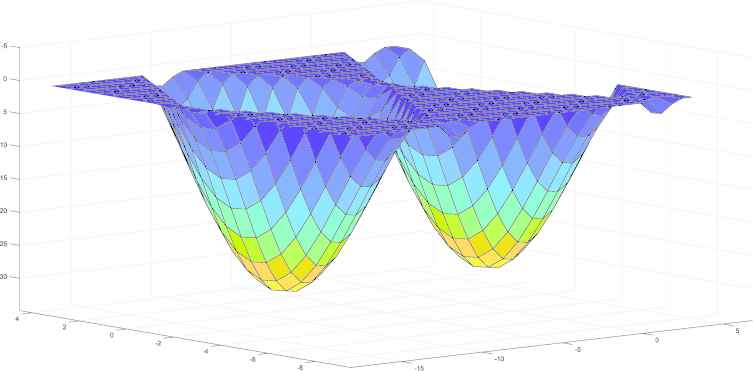
There are two minima in the energy function in this case, and the idea of the proposed model is to find the minima which are the cluster ensemble center.
Here we propose a model based on a technique from quantum mechanics where we employ the scale-space algorithm of [36] which uses a Parzen-window estimator of the probability distribution of the data points. We use a Gaussian kernel to generate probability distribution of the data points in a Euclidean space of dimension up to an overall normalization as seen in the expression
Conventionally, in quantum mechanics, the value of
From the above formula,
When the equation is solved, the cluster centers of original data can be obtained according to the base cluster labels. Then, the problem of allocating the data points to the different clusters needs to be solved, and a gradient descent algorithm can be used for this purpose.
3.4. QCE Algorithm
In general, there are two steps for cluster ensemble. One is to produce the base cluster results; the other is to design the consensus function for ensemble. The proposed model is an object-based technique where the base cluster labels are viewed as the new features of the original dataset. QCE algorithm is designed according to the proposed model. The detailed steps are shown in Algorithm 1.
Algorithm 1: Quantum clustering ensemble algorithm
Input:
Output:
1. perform Singular value decomposition on
2. normalize
3. performs gradient descent on
4. Sort the elements of
5. calculate
6. calculate the gradient of V:
7. obtain the cluster centers according to
8. assign data points to their corresponding clusters;
9. L is obtained.
The proposed algorithm complexity is
The framework of cluster ensemble is shown in Figure 2, and it can be seen that the base clustering algorithms and the correspond cluster ensemble algorithms are used in this framework.
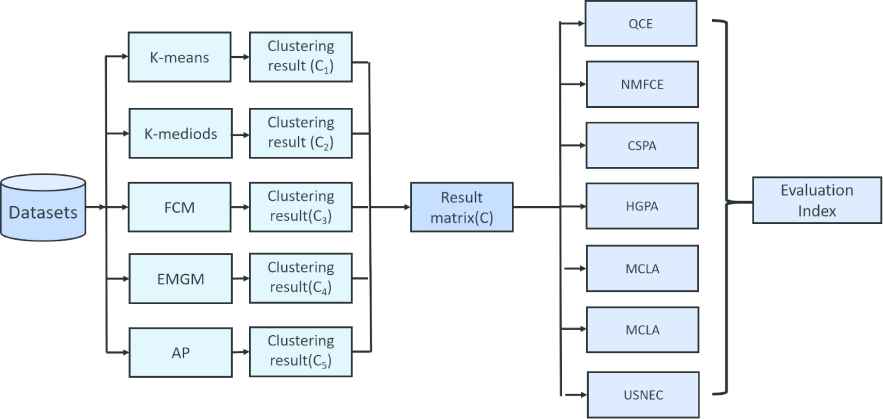
The framework of cluster ensemble and the algorithms are used in the experiments.
4. EMPIRICAL STUDY
In the following experiments, we firstly introduce the relevant datasets which verify the performance of the algorithm QCE. Secondly, we introduce the experimental settings. Thirdly, we analyze the experimental results based on the chart and figures.
4.1. Experimental Setup
We conducted comparative experiments on 12 data sets. All datasets are presented in Table 1. These datasets are obtained from UCI machine learning repository and Microsoft Research Asia Multimedia (MSRA-MM) dataset [39]. MSRA-MM dataset is distributed by MSRAMm at early March, 2009, and each image including 7 different features: (1) block-wise color moment; (2) HSV color histogram; (3) RGB color histogram; (4) color correlogram; (5) edge distribution histogram; (6) wavelet texture; and (7) face features. More information can be seen in the paper [39]. The datasets in our experiments are real and valid. Furthermore, we use Matlab 2017a software for the experiments.
| IDX | Data Set | Source | Instances | Features | Categories | Type |
|---|---|---|---|---|---|---|
| 1 | CANE | Microsoft | 1080 | 865 | 9 | Image |
| 2 | voiture | Microsoft | 881 | 892 | 3 | Image |
| 3 | wineqwsub | Microsoft | 4535 | 11 | 3 | Real |
| 4 | bathroom | Microsoft | 924 | 892 | 3 | Image |
| 5 | bugatti | Microsoft | 882 | 892 | 3 | Image |
| 6 | bus | Microsoft | 910 | 892 | 3 | Image |
| 7 | bicycle | Microsoft | 844 | 892 | 3 | Image |
| 8 | vista | Microsoft | 799 | 899 | 3 | Image |
| 9 | banner | UCI | 860 | 892 | 3 | Real |
| 10 | yeat | UCI | 1484 | 7 | 8 | Real |
| 11 | gisette_train | UCI | 6000 | 5000 | 2 | Real |
| 12 | ad | UCI | 3279 | 1558 | 2 | Real |
Description of the datasets.
In this section, we adopt the accuracy measurement [40] to evaluate the quality of the clusters. We use real labels available with the datasets as the clustering performance standard in the accuracy measurements. The accuracy estimates the matching degree between all cluster pairs, and is calculated as
4.2. Experimental Results
In the experiment section, the base cluster algorithms and the other cluster ensemble algorithms are applied as comparative algorithms to QCE.
We carry out the experiments in two steps. First, the parameter
The accuracy of the above clustering algorithms is then measured using Eq. (11). Table 2 contains the accuracy results for the control algorithm QCE and the base clustering. The best results on each dataset are indicated in bold font. The values in the table show that QCE attains the best results for 9 of the 12 datasets. FCM achieves the best result with only two datasets, and AP gives the best results with one dataset. The average results show that QCE outperforms all the base cluster algorithm with higher 8 percent.
| Dataset | QCE | FCM | EMGM | AP | ||
|---|---|---|---|---|---|---|
| CANE(1) | 0.5722 (1) | 0.5028 (2) | 0.3694 (4) | 0.2009 (6) | 0.3380 (5) | 0.4731 (3) |
| voiture(2) | 0.4688 (1) | 0.3712 (6) | 0.4132 (3) | 0.4461 (2) | 0.4064 (5) | 0.4098 (4) |
| wineqwsub(3) | 0.4629 (1) | 0.3996 (6) | 0.4002 (4) | 0.4000 (5) | 0.4388 (2) | 0.4183 (3) |
| bathroom(4) | 0.5281 (1) | 0.3734 (6) | 0.4416 (4) | 0.4578 (3) | 0.4859 (2) | 0.4221 (5) |
| bugatti(5) | 0.5476 (1) | 0.3946 (6) | 0.4859 (3) | 0.4757 (4) | 0.4941 (2) | 0.4070 (5) |
| bus(6) | 0.6275 (1) | 0.4429 (4) | 0.4824 (3) | 0.5429 (2) | 0.3648 (6) | 0.3791 (5) |
| bicycle(7) | 0.5047 (2) | 0.4336 (4) | 0.4704 (3) | 0.5308 (1) | 0.4325 (5) | 0.4313 (6) |
| vista(8) | 0.4819 (2) | 0.4731 (4) | 0.4431 (5) | 0.4919 (1) | 0.4756 (3) | 0.4393 (6) |
| banner(9) | 0.5977 (1) | 0.4802 (4) | 0.5012 (2) | 0.5000 (3) | 0.4453 (6) | 0.4535 (5) |
| yeat(10) | 0.5910 (1) | 0.4549 (5) | 0.5236 (3) | 0.4084 (6) | 0.5458 (2) | 0.5229 (4) |
| gisette_train(11) | 0.7198 (1) | 0.6852 (4) | 0.6380 (5) | 0.6892 (2) | 0.5915 (6) | 0.6887 (3) |
| ad(12) | 0.8844 (3) | 0.8900 (2) | 0.8706 (5) | 0.8817 (4) | 0.6197 (6) | 0.8984 (1) |
| Average | 0.5822 | 0.4918 | 0.5033 | 0.5021 | 0.4699 | 0.4953 |
| Average rank | 1.3333 | 4.4167 | 3.6667 | 3.2500 | 4.1667 | 4.1667 |
QCE, quantum clustering ensemble; FCM, fuzzy c-means; EMGM, expectation maximization with Gaussian mixture.
Comparison of accuracy measurements between QCE and the base clustering algorithms on 12 datasets.
After comparison of QCE to single clustering algorithms, we compared the proposed method with several states of the art clustering ensemble algorithms. Table 3 compares the accuracy values of the control algorithm QCE and the other clustering ensemble algorithms.
| Dataset | QCE | NMFCE | CSPA | HGPA | MCLA | EMCN | USENC |
|---|---|---|---|---|---|---|---|
| CANE(1) | 0.5722 (2) | 0.4185 (4) | 0.4157 (5) | 0.2856 (6) | 0.2426 (7) | 0.4407 (3) | 0.5944(1) |
| voiture(2) | 0.4688(1) | 0.3746 (7) | 0.4132 (3) | 0.3844 (6) | 0.4109 (4) | 0.4359 (2) | 0.3905(5) |
| wineqwsub(3) | 0.4629 (1) | 0.4362 (2) | 0.3980 (4) | 0.3866 (7) | 0.4075 (3) | 0.3968 (6) | 0.3967(5) |
| bathroom(4) | 0.5281 (1) | 0.3485 (6) | 0.3463 (7) | 0.4475 (2) | 0.3907 (4) | 0.4091 (3) | 0.3712(5) |
| bugatti(5) | 0.5476 (1) | 0.3805 (6) | 0.3848 (5) | 0.4476 (3) | 0.3680 (7) | 0.4618 (2) | 0.4127(4) |
| bus(6) | 0.6275 (1) | 0.4385 (4) | 0.4143 (5) | 0.3823 (7) | 0.4011 (6) | 0.5374 (2) | 0.4495(3) |
| bicycle(7) | 0.5047 (1) | 0.4645 (3) | 0.4147 (6) | 0.3757 (7) | 0.4633 (4) | 0.4692 (2) | 0.4369(5) |
| vista(8) | 0.4819 (2) | 0.4844 (1) | 0.4406 (6) | 0.4255 (7) | 0.4681 (3) | 0.4581 (5) | 0.4681(4) |
| banner(9) | 0.5977 (1) | 0.3686 (6) | 0.3430 (7) | 0.4763 (3) | 0.4802 (2) | 0.4721 (4) | 0.4616(5) |
| yeat(10) | 0.5910 (1) | 0.5472 (3) | 0.4346 (6) | 0.3544 (7) | 0.4805 (5) | 0.5681 (2) | 0.5445(4) |
| gisette_train(11) | 0.7198 (1) | 0.7033 (2) | 0.6867 (4) | 0.5093 (6) | 0.6815 (5) | 0.5000 (7) | 0.6987(3) |
| ad(12) | 0.8844 (2) | 0.8775 (4) | 0.5962 (6) | 0.5002 (7) | 0.8651 (5) | 0.8872 (1) | 0.8805(3) |
| Average | 0.5822 | 0.4868 | 0.4407 | 0.4146 | 0.4716 | 0.5030 | 0.5088 |
| Average rank | 1.2500 | 4.0000 | 5.3333 | 5.6667 | 4.5833 | 3.2500 | 3.9167 |
QCE, quantum clustering ensemble; CSPA, cluster-based similarity partitioning algorithm; HGPA, hyper-graph partitioning algorithm; MCLA, meta-clustering algorithm; NMFCE, nonnegative matrix factorization for clustering ensemble; USENC, ultra-scalable ensemble clustering.
Comparison of accuracy between QCE and ensemble clustering algorithms on 12 datasets.
The results in Table 3 show that the QCE algorithm realizes the best result with 10 of the 12 datasets. NMFC does best with one dataset, and EMCN gives the best result once. CSPA, HGPA, and MCLA produced inferior performance in comparison to NMFCE with all of the datasets.
Under the null hypothesis, statistical test is good way to differentiate the algorithms and to find out the p-value [47–49] among the algorithms. In order to test the true difference of results between the proposed algorithm and the comparing algorithms, Friedman test [50] is used for statistical tests. Friedman test is a two-way analysis of variances by ranks, and its objective is to determine if we may conclude from a sample of results that there is difference among treatment effects.
The first step in calculating the test statistic is to convert the original results to ranks. Thus, it ranks the algorithms for each problem separately, the best performing algorithm should have the rank of 1, the second best rank 2, etc., as shown in Tables 2 and 3. In case of ties, average ranks are computed, and the less ranks, the better results.
Let
With 6 algorithms and 12 data sets,
For Table 3, the Friedman test proves whether the measured average ranks are significantly different from the mean rank
With 7 algorithms and 12 data sets,
5. CONCLUSIONS
Ensemble learning can improve the performance of machine learning algorithms, and clustering ensemble is a typical unsupervised ensemble learning to combine several base clusters as a final clustering result, and it can be used for knowledge reuse, distributed computing, and privacy preserve. In this article, we proposed a novel clustering ensemble technique derived from quantum mechanics where the base clustering results are viewed as new features of the original dataset. Then, a scale-space probability function is constructed from the given data points. This function can then be optimized to obtain the minima result, which can determine the centers. Furthermore, several datasets were used for experiments and the results show the proposed algorithm strength against the state of the art algorithms and more interestingly, it outperformed some of the state of the art algorithms. On the other way, QCE requires the base cluster ensemble results to be transformed in Hilbert space which is the limitation of the proposed algorithm and it just runs on a single computer for its performance, while a parallel and distributed QCE can be designed to run on a computer cluster for processing big data in the future.
CONFLICTS OF INTEREST
There is no conflict of interest for all authors in this paper.
AUTHORS' CONTRIBUTIONS
literature search: Peizhou Tian and Shuang Jia, study design: Ping Deng, manuscript writing: Peizhou Tian and Shuang Jia, data collection and data analysi: Hongjun Wang.
ACKNOWLEDGMENTS
This research was supported by the National Key R and D Program of China (No. 2017YFB1401401), and Nature Science Foundation of China (No. 81373056), and partly by the Key program for International S and T Cooperation of Sichuan Province (No. 2019YFH0097). We thank the anonymous reviewers for their helpful comments and suggestions.
REFERENCES
Cite this article
TY - JOUR AU - Peizhou Tian AU - Shuang Jia AU - Ping Deng AU - Hongjun Wang PY - 2020 DA - 2020/11/25 TI - Quantum Clustering Ensemble JO - International Journal of Computational Intelligence Systems SP - 248 EP - 256 VL - 14 IS - 1 SN - 1875-6883 UR - https://doi.org/10.2991/ijcis.d.201119.001 DO - 10.2991/ijcis.d.201119.001 ID - Tian2020 ER -
