Induced Dynamics
- DOI
- 10.1080/14029251.2020.1700648How to use a DOI?
- Keywords
- complete integrability; dynamics of singularities; Calogero–Moser system; Ruijsenaars–Schneider system
- Abstract
Construction of new integrable systems and methods of their investigation is one of the main directions of development of the modern mathematical physics. Here we present an approach based on the study of behavior of roots of functions of canonical variables with respect to a parameter of simultaneous shift of space variables. Dynamics of singularities of the KdV and Sinh–Gordon equations, as well as rational cases of the Calogero–Moser and Ruijsenaars–Schneider models are shown to provide examples of such induced dynamics. Some other examples are given to demonstrates highly nontrivial collisions of particles and Liouville integrability of induced dynamical systems.
- Copyright
- © 2020 The Authors. Published by Atlantis and Taylor & Francis
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. Introduction
Let 𝒜N denote a phase space of N-particle one dimensional dynamical system with coordinates qi and momenta pi, i = 1,...,N, canonical with respect to the Poisson bracket {qi, pj} = δij. Let H = H(q, p) denote the Hamiltonian of this system, where q = (q1,...,qN), p = (p1,..., pN), i.e.,
The induced system is not only Hamiltonian but also integrable, as by construction it has (at least) N integrals of motion in involution.
Assume, that (q, p) ∈ 𝒜′N, i.e., there exists exactly N real (different) solutions of the Eq. (1.1):
Taking (1.3) into account we differentiate (1.4) twice with respect to t:
One can consider (1.4) and (1.5) as system of 2N equations on 2N unknowns q and p, that are defined by means of these equations as functions of x and ẋ under condition of unique solvability of this system, that we assume below. Inserting these functions in (1.6) we prove existence of the Newton-type equations of the induced dynamical system:
The above consideration gives also scheme of solution of the Cauchy problem for the induced system. Let we are given with 2N initial data: xi(0) and ẋj(0), say at t = 0, where i, j = 1,...,N. Equations (1.4) and (1.5) define values (q(0), p(0)) that belong to 𝒜′N by definition. Then by (1.3) qi(t) = qi(0) + th′(pi), pi(t) = pi, that after substitution in (1.1) gives M real roots x1(t),...,xM(t) for any t ∈ ℝ. Thus the scheme of solution of the Cauchy problem for the induced dynamical system is close to the one for integrable nonlinear PDE’s. Notice that M is not obliged to be equal to N at any moment of time, i.e., point (q(t), p(t)) is not obliged to belong to 𝒜′N for any t.
Below we demonstrate that in spite of a trivial dynamics of the system on the phase space 𝒜, dynamics of the induced system is highly nontrivial. In particular, it demonstrates effects that can be interpreted as existence of stable bound states and even as creation and annihilation of particles.
The manuscript is organized as follows. In Sec. 2 we consider dynamical systems that appeared many years ago (see, e.g., [1], [11], [12], [13], and [14]) as systems describing the dynamics of singularities of solutions of some integrable equations (“zeros” of τ-functions). While ideology developed here is based essentially on study of the singular solutions of the Liouville equation in [12] and [13], here we consider more interesting dynamics of singularities of soliton solutions of the KdV and Sinh–Gordon equations and show that this dynamics is the induced one. In Sec. 3 we derive a new determinant formula for solutions of the well known dynamical systems: rational Calogero–Moser, [3, 4], and Ruijsenaars–Schneider, [16, 17], models. By these means dynamics of these systems also can be described as the induced one, that explicitly demonstrates their Liouville integrability. We also suggest some integrable generalizations of these models. In Sec. 4 we present some other simple examples of the induced systems given by polynomial functions f in (1.1), both in nonrelativistic and relativistic cases. Results and possible developments of the suggested technique are discussed in Sec. 5. Properties of the induced systems under consideration are displayed by means of figures carried out by package Wolfram Mathematica 11.1.
2. Dynamics of singularities of solutions of integrable differential equations
2.1. Singular solutions of the KdV equation
In this section we show that old results on dynamics of singularities of soliton solutions (singular solitons) of integrable PDE’s can be formulated in terms of induced dynamics. We start with N-soliton solution of the KdV equation 4ut − 6uux + uxxx = 0 on a real function u(t, x), where indexes denote partial derivatives. This famous equation is known to have both regular (see, e.g., [8]) and singular (see [1]) N-soliton solutions. Their generic form is given by
Here ai, pi, and εi = ±1, i = 1,...,N, are constant parameters of the solution such that Re pi > 0 and
If Im pi = 0 signs εi = +1 and εi = −1 correspond to the regular and singular solitons. Every pair of
Notice now that introducing functions
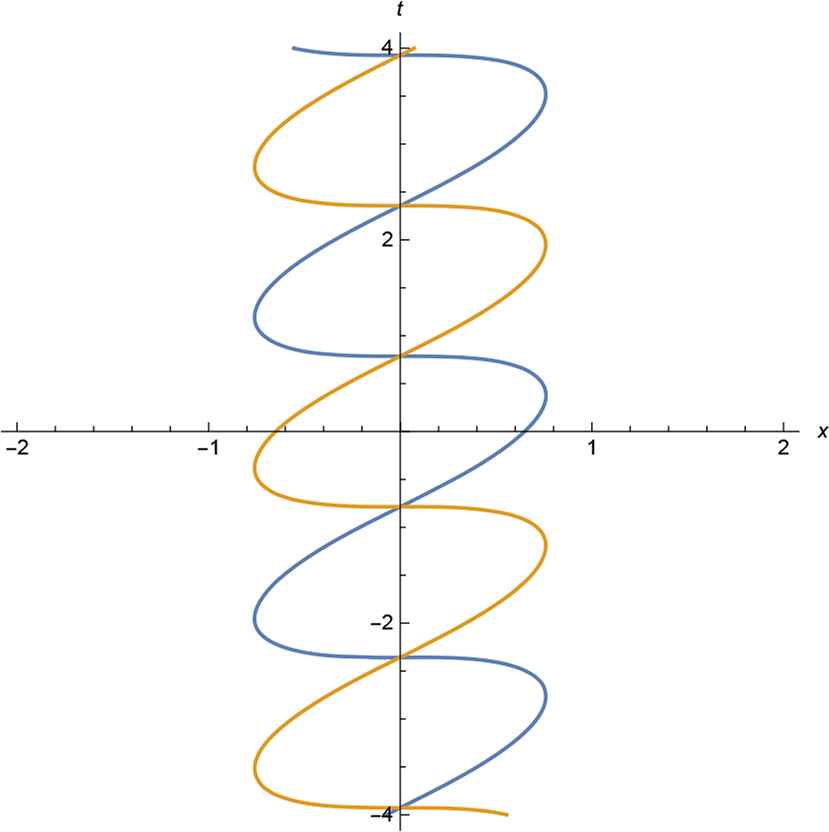
KdV: Soliton–soliton collision: ε1 = ε2 = 1.
KdV: Soliton–antisoliton collision: ε1 = −ε2
KdV: breather
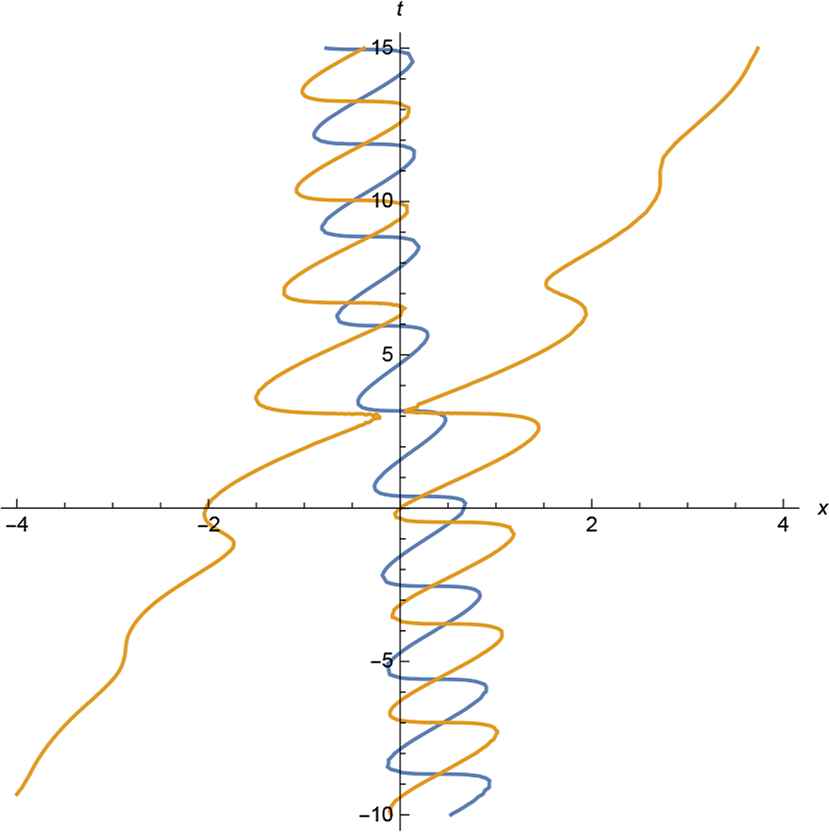
KdV: soliton–breather collision
2.2. Singular solutions of the Sinh–Gordon equation
Analogous consideration is applicable in the relativistic case. We consider a dynamical system determined by motion of singularities of the soliton solutions of the Sinh–Gordon equation, utt − uxx + sinhu = 0, on the real function u(t, x). Its N-soliton solution is given, [12] and [14], by
These zeros form N smooth time-like curves ξi(η), i = 1,...,N, their behavior is close to that on Figs. 1–4, see [11], [12] and [14] for detail.
Setting
Eq. (2.12) coincides with (1.1) with f given in (2.6) up to substitution x → ξ, t → η, but dynamics on the space 𝒜 is given here by
System (2.12) with function f(q, p) in (2.13) is invariant with respect to the Lorentz boost:
3. Rational cases of the Calogero–Moser and Ruijsenaars–Schneider models
Here we show that the rational versions of the Calogero–Moser (CM) and Ruijsenaars–Schneider (RS) models also give examples of the induced dynamics, i.e., their solutions are given as roots of Eq. (1.1) with proper choices of functions f(q, p) and h in (1.1) and (1.2). Dynamics of these models, see [3, 7, 16, 17], is given by equations
It was also proved there that, say, at t → −∞ this solutions obey asymptotic behavior
In order to prove that CM and RS systems can be written in the form (1.1), we notice that because of the translation invariance, solutions xi(t) are roots of the characteristic equation
Now for the term (t − τ)V(τ) (see (3.3) and (3.4)) we have in the limit (3.6):
Thus solutions of the rational versions of CM and RS models are given by the roots of the equation
Eqs. (3.9)–(3.11) in their turn enables derivation of the known Lax representations for the both these models following the same lines like in [9] and [18]. In particular, we get that momenta pi are eigenvalues of the Lax matrix (3.3).
Characteristic equation (3.9) is exactly of the form (1.1), where f(q, p) = det(Q +W),
4. Polynomial examples of induced dynamics
In this section we consider some simplest examples of induced dynamical systems, given by polynomial function f in (1.1):
Here C is a real constant (parameter of the system), variables qi and pi obey condition of reality, given in the beginning of Sec. 1 and
Such systems are more trivial then those considered in Sec. 2. Say, they do not give nontrivial phase shifts. Nevertheless, examples of N = 2 and N = 3 of these system and their relativistic analogs (see Sec. 4.2 below) demonstrate such unexpected for classical mechanics effects as creation/annihilation of particles. Notice that here we do not impose conditions of the kind Re pi > 0 in (2.3) on variables in 𝒜N.
4.1. Nonrelativistic case
Let us start with N = 2 in (4.1), i.e., with function f(q, p) = q1q2 − C/4, that also coincides with the N = 2 case of (3.9), where matrix 2×2-matrix W is off-diagonal and p-independent. Eq. (1.1) in this case sounds as
Eqs. (4.5) and (4.6) define qi and pi in terms of xi and ẋi (cf. (1.5), (1.6)). These values, being substituted in the time derivative of (4.6) gives explicit equations of motion of the induced dynamical system, cf. (1.7):
It is worth to mention that under reduction to the center of mass frame,
Eqs. (4.7) are Lagrangian with
Variables qi and pi are canonically conjugate, and due to (4.5) we get {xi, xj} = 0. Then (4.8) enables to introduce momenta conjugate to xi as
In order to show behavior of the world lines of the particles on the (x, t)-plane we consider initial problem: xi(t)|t=0 = ai, ẋi(t)|t=0 = vi, where x0,i and vi are real initial data. These data define qi(0) and pi(0) by Eqs. (4.5) and (4.6). Because of the free evolution on 𝒜2, we have that qi(t) = qi(0) + pit, pi(t) = pi, and finally we reconstruct xi(t) by (4.5):
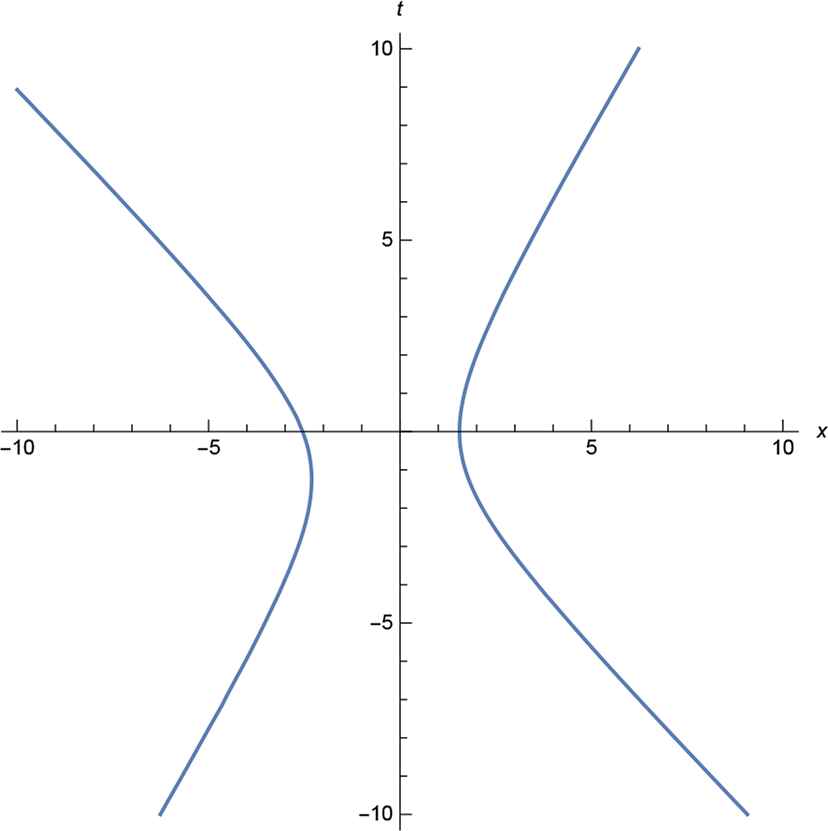
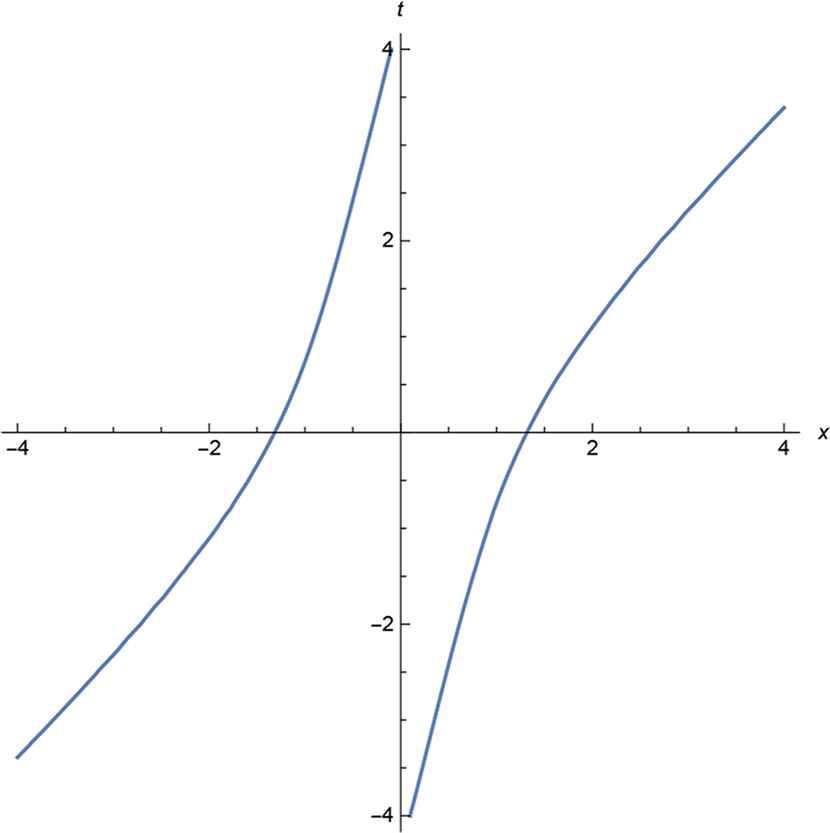
Two particles,
Two particles,
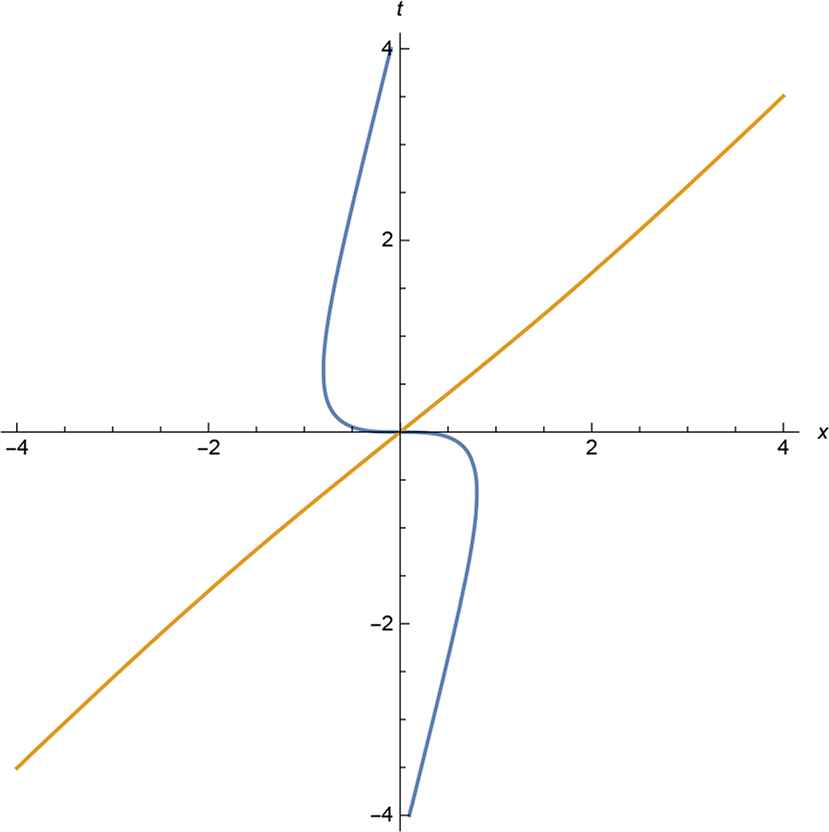
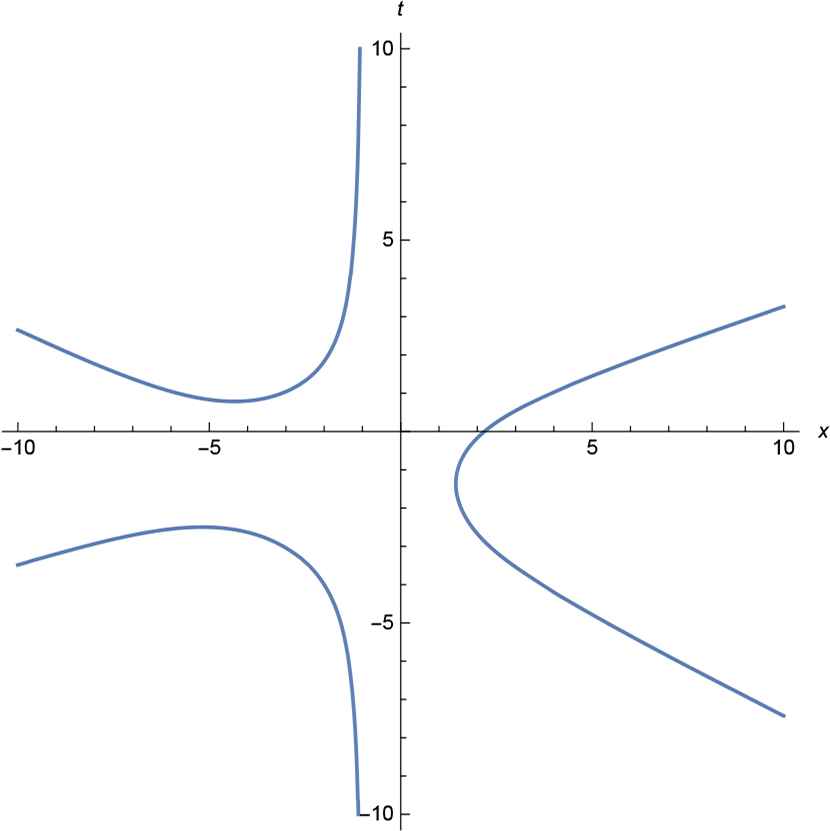
If the induced system is given by (4.3) with C < 0, we always have
Two particles, C < 0
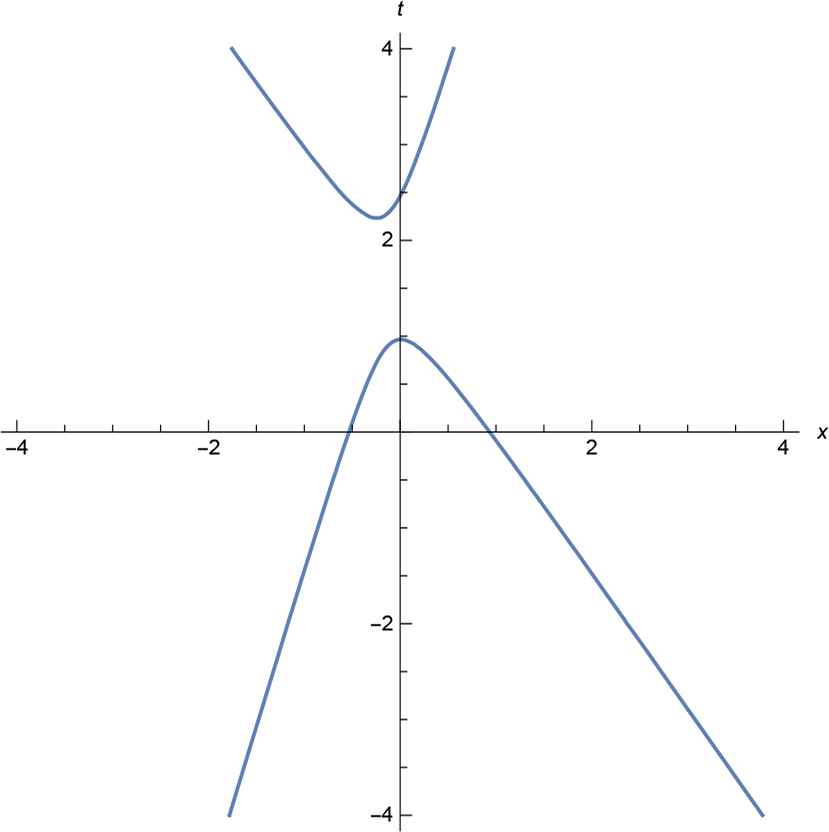
Analogously one can consider the higher values of N in (4.1). Say, on the Fig. 8 we present structure of the world lines of the system, given by N = 3 in (4.1). By no means this structure is very unexpected for dynamical systems: three particles descend from infinity, two of them annihilate and for a period induced system has only one particle (only one real solution of the equation of the third order). Nevertheless, motion of this particle is far from being free: it slows down, stops and turns back.
Three particles.
4.2. Relativistic case.
As we discussed in Sec. 3 relativistic induced system is defined by function f(q, p) invariant with respect to the Lorentz boost (2.15). Say, in the case N = 2 we can define such system by means of equation
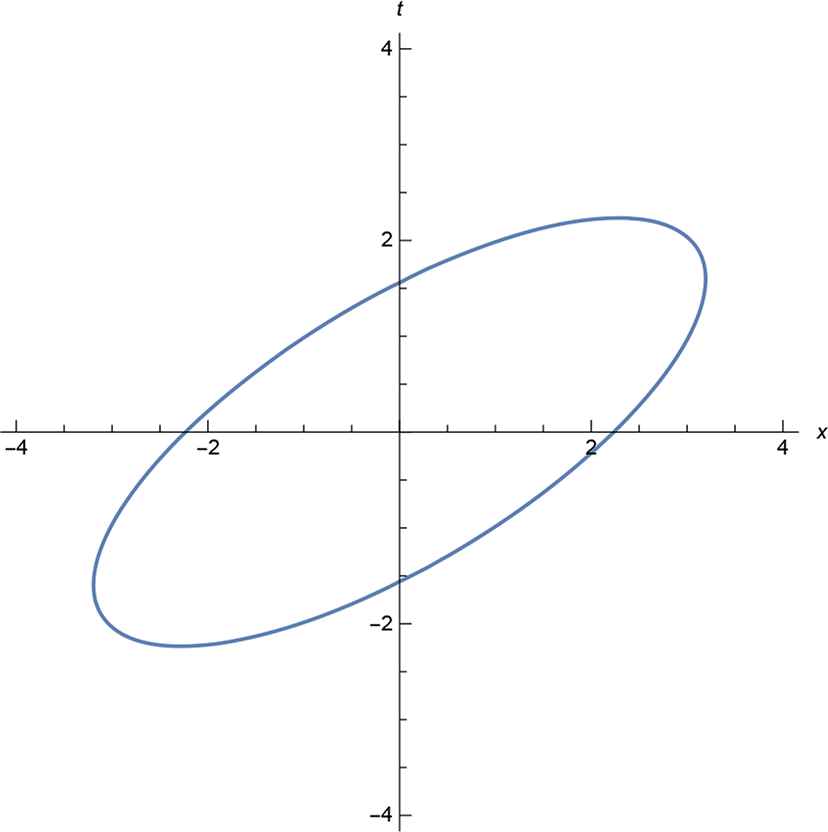
Behavior of the world lines of this system on the (x, t)-plane is determined by the sign of the product C[(ξ1 − ξ2) 2 + (ξ′1 + ξ′2)C], that is preserved under evolution (4.14). It is necessary to take into account that in cone variables (2.9) condition on a world line to be time-like sounds as ξ′i < 0. In the case where the product is positive, we get behavior of the world lines close to the one on Fig. 5, where both lines are time-like.
5. Concluding remarks
The idea to construct dynamical systems by means of the relationship among the zeros and coefficients of time-dependent polynomials (or possibly more general functions, for instance entire ones) is rather old, [4]. It was essentially developed later, see, e.g., [5] and references therein. This approach can be considered as a version of induced dynamics as well—the dynamics of the zeros is induced by the dynamics of the coefficients of polynomials—in fact more general than considered above. The main difference between this general approach and the notion of induced dynamical systems introduced in this article is the Liouville integrability of the latter ones. Say, coefficients of polynomial f(q − x 1, p) for dynamical system defined by (4.1) are given in terms of elementary symmetric polynomials of qi and for a generic N evolution equations of these coefficients are neither explicit, nor give any information on integrability, in contrast to (4.2).
Induced dynamical systems of Sec. 2 were originated by the singular soliton solutions of the integrable equations, KdV and Sinh–Gordon. Thus it was natural to expect their Liouville integrability. Integrability of the CM and RS system is well known also. Unexpected result of our consideration in Secs. 2 and 3 is the existence of rich families of integrable models beyond these known ones. Thus functions f in (2.6) and (2.13) define, thanks to Eqs. (2.5) and (2.14), integrable systems not only in the case where matrix v is given by (2.2), but for an arbitrary matrix v(p). The same is valid for matrices W in Sec. 3, that are not obliged to be given by (3.11) in order to generate integrable dynamical systems by means of (3.9). Examples from Sec. 4 show that cases where forces in the r.h.s. of (1.7) are explicit are very rare, and in generic situation investigation of induced systems must be based on the description of solutions of Eq. (1.1). Properties of the induced dynamical systems (4.7) and (4.14) look to be rather strange, they are new to our knowledge and deserve further investigation. Summarizing results of Sec. 4, we see that the dynamical system on the space 𝒜N (i.e.,
In this article we suggested notion of the induced dynamical system and proved that it gives effective method to investigation of known systems and to construction of new ones. These systems demonstrate rather nontrivial particle interactions being completely integrable by construction. Some other examples of the induced systems were presented in the preliminary version of this article, see [15]. It is also interesting to generalize consideration of the Sec. 2—dynamics of singularities of the nonlinear equations—to the case where solitons are unstable and, say, collision of two regular solitons leads to a singularity. Such soliton solutions were studied in [10], [6], and [2], in particularly for the case of the Boussinesq equation.
Acknowledgment
Author thanks G. Arutyunov, L.V. Bogdanov, F. Calogero, A.M. Liashyk, S. Ruijsenaars, and A.V. Zotov for fruitful discussions. The work is supported in part by the Russian Academic Excellence Project ‘5-100’ and by the grant RFBR # 18-01-00273.
References
Cite this article
TY - JOUR AU - A. K. Pogrebkov PY - 2020 DA - 2020/01/27 TI - Induced Dynamics JO - Journal of Nonlinear Mathematical Physics SP - 324 EP - 336 VL - 27 IS - 2 SN - 1776-0852 UR - https://doi.org/10.1080/14029251.2020.1700648 DO - 10.1080/14029251.2020.1700648 ID - Pogrebkov2020 ER -
