1. INTRODUCTION

Non-photorealistic rendering is a field of computer graphics that can generate effective illustrations and attractive artistic images. Some researchers have proposed non-photorealistic rendering methods to simulate art expression techniques and to develop unprecedented artistic approaches [1–7]. One of the unprecedented artistic approaches is a method to generating cell-like images by an iterative calculation using inverse iris filter from photographic images [8]. Cell-like patterns are composed of cell membrane and cell nucleus. Cell-like images are overlaid with cell-like patterns in photographic images. Cell patterns are automatically generated by the change of density of photographic images. However, cell-like patterns are irregularly arranged. Therefore, a method for aligning cell-like patterns in cell-like images has been proposed [9]. The conventional method [9] is implemented by synthesizing sine and cosine waves into photographic images. However, in the conventional method [9], cell-like patterns are mainly arranged in a grid pattern, and therefore the edge preservation of cell-like images is not high. Also, the actual cells are not arranged in the grid pattern.

In this paper, we propose a method to arrange cell-like patterns along the edges of photographic images. Our method also has the feature that the cell membrane and cell nucleus in cell-like patterns can be expressed more clearly than the conventional methods [8,9]. We improve the conventional method [8] by using Euclidean distance from the edges. Cell-like images of our method can give an impression different from cell-like images of the conventional methods [8,9]. By conducting experiments using various photographic images, it is visually confirmed that cell-like patterns can be generated along the edges and cell-like patterns that express the cell membrane and cell nucleus more clearly than the conventional methods [8,9] are generated. In addition, it is visually confirmed that the size of cell-like patterns can be changed by changing the values of the parameters in our method.

This paper is organized as follows: Section 2 describes our method to arrange cell-like patterns along the edges, Section 3 shows experimental results and reveals the effectiveness of our method, and the conclusion of this paper is given in Section 4.

2. OUR METHOD

Our method is implemented in two steps. In the first step, distance-transformed images are created by calculating Euclidean distance from the edges of photographic images. In the second step, cell-like images are generated using distance-transformed images and inverse iris filter. Inverse iris filter is calculated by the procedure that restores the transformed image using iris filter [10] to the original image using inverse filter [11]. The flow chart of our method is shown in Figure 1.

We explain details of the procedure in Figure 1.

Figure 1

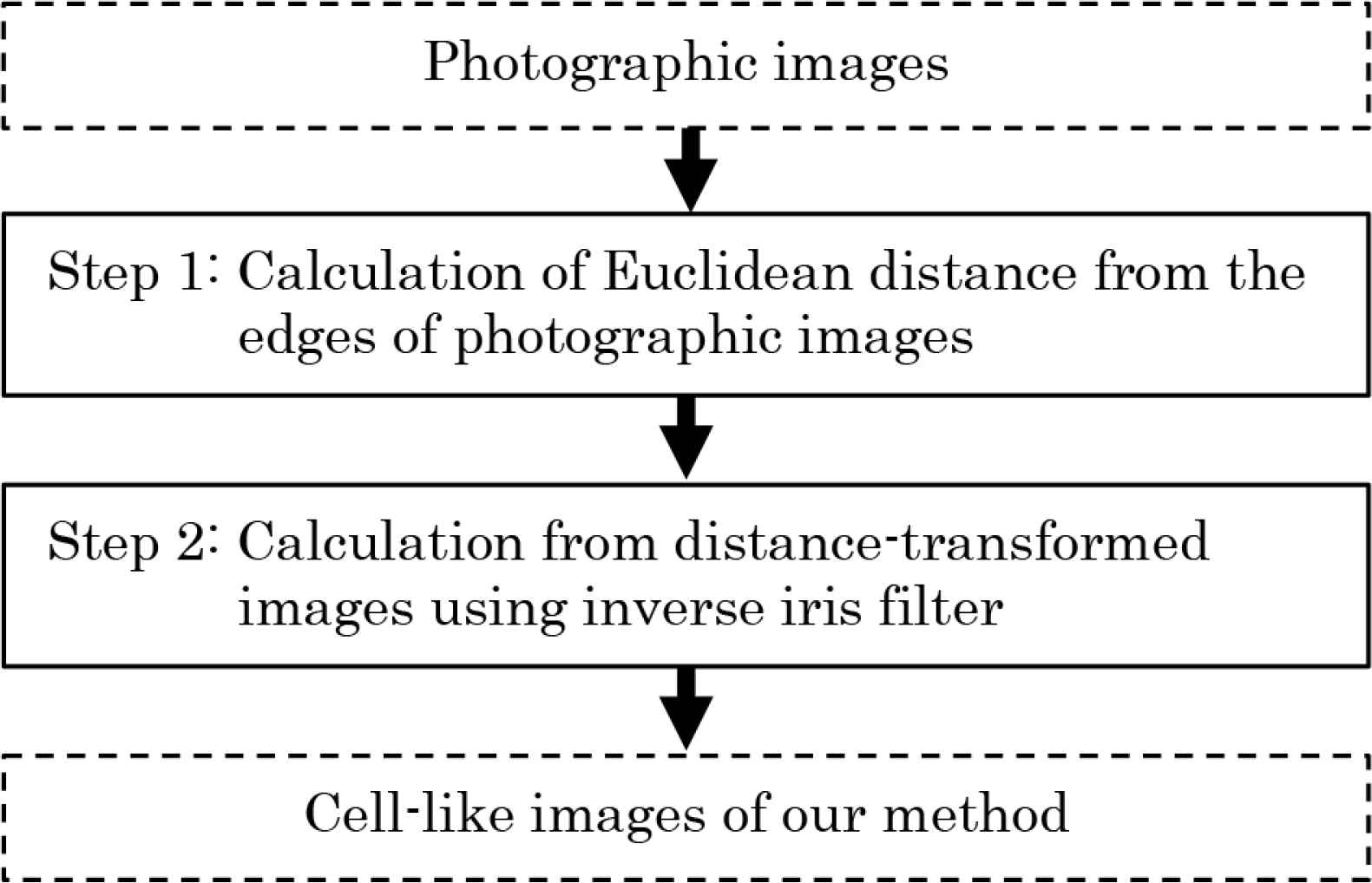
Flow chart of our method.

Step 0: Let input pixel values of RGB on coordinates (i,j) in a color photographic image be f_R,i,j, f_G,i,j and f_B,i,j (i = 1, 2, 3, …, I; j = 1, 2, 3, …, J). The pixel values f_R,i,j, f_G,i,j and f_B,i,j have value of U gradation from 0 to U − 1.

Step 1: Gray-scale pixel values f_i,j are calculated as follows.

Edges are extracted from the gray-scale image using EDISON [12] that is a feature extraction tool that integrates edge detection and image segmentation. Shortest Euclidean distances d_1,i,j from the edge pixels are calculated at each pixel.

If the Euclidean distances d_1,i,j are within mD + D/2 ± 0.5(m = 0, 1, 2, …), the Euclidean distances d_2,i,j are set to 0, where D is a positive constant. Otherwise, the Euclidean distances d_2,i,j are set to ∞. When the positions where the Euclidean distances d_2,i,j are 0 are expressed on the image, it becomes lines of the interval D along the edges.

Scan from the upper left to the lower right of the image, and in the case that the Euclidean distance d_2,i,j are 0 at the target pixel (i,j), the Euclidean distances d_2,k,l in the range where the Euclidean distance from the target pixel (i,j) is smaller than D are updated to ∞. Where the pixels (k,l) have the Euclidean distances from the target pixel (i,j) smaller than D, and the Euclidean distance d_2,i,j of the target pixel (i,j) is not updated. When the positions where the Euclidean distances d_2,i,j are 0 are expressed on the image, it becomes dotted lines with the spacing D.

Scan from the upper left to the lower right of the image, and in the case that the Euclidean distance d_2,i,j are ∞ at the target pixel (i,j), the Euclidean distance d_2,i,j of the target pixel (i,j) is updated to 0 if there is no pixel where the Euclidean distances d_2,k,l are 0 in the range where the Euclidean distance from the target pixel (i,j) is smaller than D. In all pixels (i,j), there are pixels that the Euclidean distances d_2,k,l are 0 within the radius D. Shortest Euclidean distances d_i,j from the pixels that the Euclidean distances d_2,k,l are 0 are calculated at each pixel. An image composed of the shortest Euclidean distances d_i,j is called a distance-transformed image.

Step 2: Let output pixel values after processing with iris filter on d_i,j be IF(d_i,j). Iris filter is executed with the 2r + 1 peripheral pixels (k,l) in the window of size r. Angles θ_i,j,k,l between a vector (i − k, j − l) from the peripheral pixels (k,l) to the target pixel (i,j) and a vector ((d_k+2,l+2 + d_k+2,l+1 + d_k+2,l + d_k+2,l−1 + d_k+2,l-2) − (d_k−2,l+2 + d_k−2,l+1 + d_k−2,l + d_k−2,l–1 + d_k−2,l-2), (d_k+2,l+2 + d_k+1,l+2 + d_k,l+2 + d_k−1,l+2 + d_k-2,l+2) − (d_k+2,l−2 + d_k+1,l−2 + d_k,l−2 + d_k−1,l−2 + d_k−2,l-2)) are computed. Let convergence indices of the target pixel (i,j) be c_i,j. The convergence indices c_i,j are calculated as follows.

Let minimum and maximum values of c_i,j in all pixels be c_min and c_max, respectively. The convergence indices c_i,j are converted to C_i,j as follows.

The values IF(d_i,j) and C_i,j are the same.

Pixel values g_R,i,j, g_G,i,j and g_B,i,j are computed by using inverse iris filter as follows.

where a is positive constant. If g_R,i,j, g_G,i,j and g_B,i,j are less than 0, then these values must be set to 0, respectively. If g_R,i,j, g_G,i,j and g_B,i,j are greater than U − 1, then these values must be set to U − 1, respectively. The image composed of the pixel values g_R,i,j, g_G,i,j and g_B,i,j is a cell-like image of our method.

3. EXPERIMENTS

We conducted three experiments. In the first experiment, we visually confirmed the appearance of cell-like images generated from Lenna image shown in Figure 2 by changing the values of the parameters. In the second experiment, we applied our method to six photographic images in (Figure 3). All photographic images used in the experiments comprised 512 * 512 pixels and 256 gradations. In the third experiment, we visually compared cell-like patterns generated by our method and the conventional methods [8,9]. For reference, the edge extracted image and the distance-transformed image (D = 15) of Lenna image are shown in Figure 4a and 4b, respectively.

Figure 2

Lenna image.

Figure 3

Various photographic images.

Figure 4

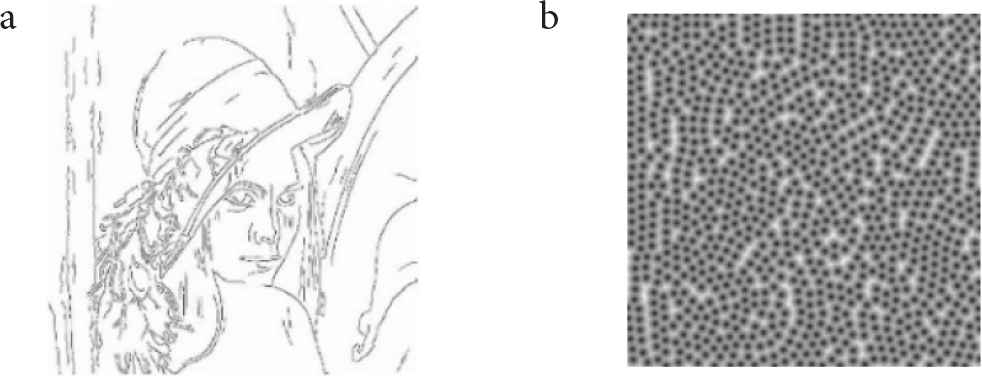
Edge-extracted image and distance-transformed image. (a) Edge-extracted image. (b) Distance-transformed image.

4. CONCLUSION

We proposed a method to arrange cell-like patterns along the edges of photographic images. We improved the conventional method [8] by using Euclidean distance from the edges of photographic images. We demonstrated the effectiveness of our method through experiments using various photographic images. The experimental results showed that our method can express cell-like patterns along the edges and can express cell-like patterns with the cell membrane and cell nucleus in cell-like patterns more clearly than the conventional methods [8,9]. In addition, the experimental results showed that the size of cell-like patterns can be changed by changing the values of the parameters in our method.

In future work, we will try to apply our method to videos and three-dimensional data.

CONFLICTS OF INTEREST

The authors declare they have no conflicts of interest.

ACKNOWLEDGMENT

This work was supported by JSPS KAKENHI Grant Number JP19-K12664.

AUTHORS INTRODUCTION

Dr. Toru Hiraoka

He graduated Doctor course at Design in Kyushu Institute of Design. He is a Professor in the Faculty of Information Systems in University of Nagasaki. His current research interests are non-photorealistic rendering and disaster prevention.

Mr. Kohei Maeda

He is a student in the Faculty of Information Systems in University of Nagasaki. His current research interests are non-photorealistic rendering and image processing.