On the Characterizations of Chen’s Two-Parameter Exponential Power Life-Testing Distribution
- DOI
- 10.2991/jsta.2018.17.3.1How to use a DOI?
- Keywords
- 60E05; 62E10; 62E15; 62G30
- Abstract
Characterizations of probability distributions play important roles in probability and statistics. Before a particular probability distribution model is applied to fit the real world data, it is essential to confirm whether the given probability distribution satisfies the underlying requirements by its characterization. A probability distribution can be characterized through various methods. In this paper, we provide the characterizations of Chen’s two-parameter exponential power life-testing distribution by truncated moment.
- Copyright
- © 2018, the Authors. Published by Atlantis Press.
- Open Access
- This is an open access article under the CC BY-NC license (http://creativecommons.org/licences/by-nc/4.0/).
1. Introduction
As pointed out by Glänzel [8], the characterizations of probability distributions may serve as the basis for parameter estimations of a probability distributions. Before a particular probability distribution model is applied to fit the real world data, it is essential to confirm whether the given probability distribution satisfies the underlying requirements by its characterizations. Thus, characterizations of a probability distribution play important role in probability and statistics. A probability distribution can be characterized through various methods, see, for example, Ahsanullah et al. [3], and references therein. For an extensive survey on characterizations of univariate continuous distributions, the interested readers are referred to a recent monograph by Ahsanullah [2], and references therein.
In recent years, there has been a great interest in the characterizations of probability distributions by truncated moments. For example, the development of the general theory of the characterizations of probability distributions by truncated moment began with the work of Galambos and Kotz [7]. Further development on the characterizations of probability distributions by truncated moments continued with the contributions of many authors and researchers, among them Kotz and Shanbahag 11], Glänzel [8], and Glänzel et al. [9], are notable. However, most of these characterizations are based on a simple proportionality between two different moments truncated from the left at the same point. In this paper, we have considered a two-parameter exponential power life-testing distribution introduced by Chen [5], and provided its characterizations by truncated moment method. For other types of exponential power life-testing distributions and their various properties, studied by other authors and researchers, the interested readers are referred to Smith and Bain [16], Leemis [13], Rajarshi and Rajarshi [15], and Chen [4], among others.
The paper is organized as follows. In Section 2, the two-parameter exponential power life-testing distribution introduced by Chen [5], and some of its properties are discussed. We present characterization results in Section 3. Finally, concluding remarks are presented in Section 4.
2. Chen’s Two-Parameter Exponential Power Life-Testing Distribution
As introduced by Chen [5], a positive continuous random variable X is said to have a two-parameter exponential power distribution with scale parameter λ > 0 and shape parameter κ > 0, which we will denote later as X ~ chenexponentialpower (λ, κ), if its probability density function is given by
The cumulative distribution function of X ~ chenexponentialpower (λ, κ) is given by
For some selected values of the parameters, the graph of probability density function (2.1) and the cumulative distribution function (2.2) are illustrated in Figures 2.1 and 2.2 respectively. From these figures it appears that the proposed distribution is right skewed.
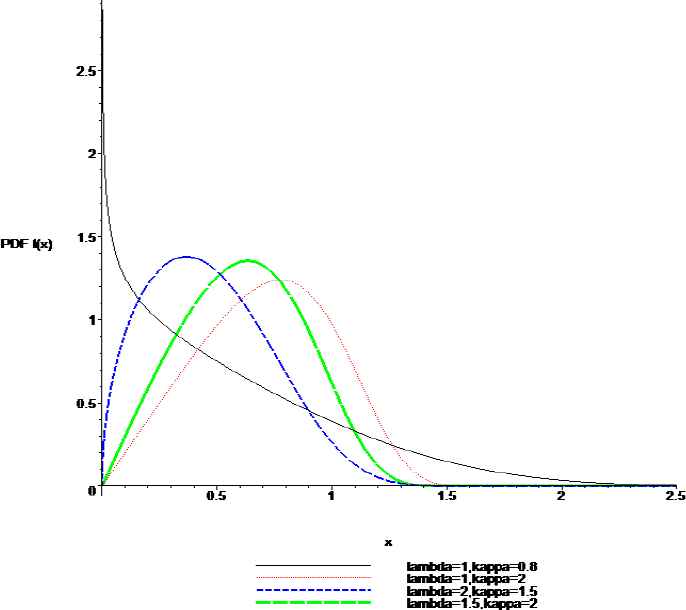
pdf, f(x), when X ~ chenexponentialpower (λ, κ).
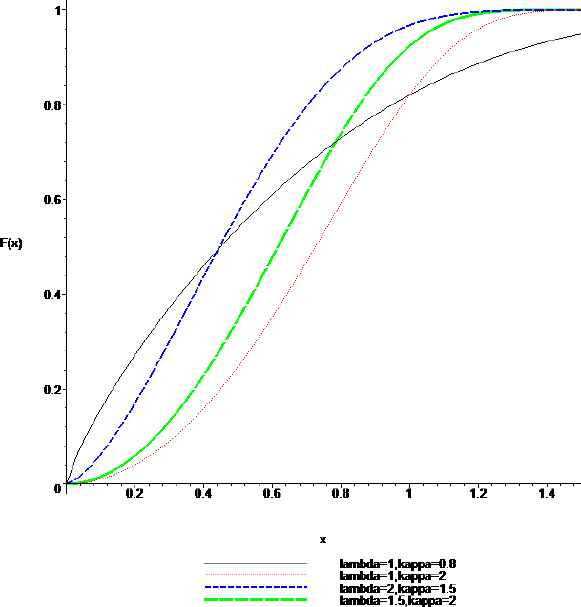
cdf, F(x), when X ~ chenexponentialpower (λ, κ).
The corresponding survival (or reliability) and the hazard (or failure rate) functions, at any time, x > 0, are respectively given by
For some selected values of the parameters, the graph of hazard function (2.4) is illustrated in Figure 2.3 and it appears that hazard function has bathtub-shaped.
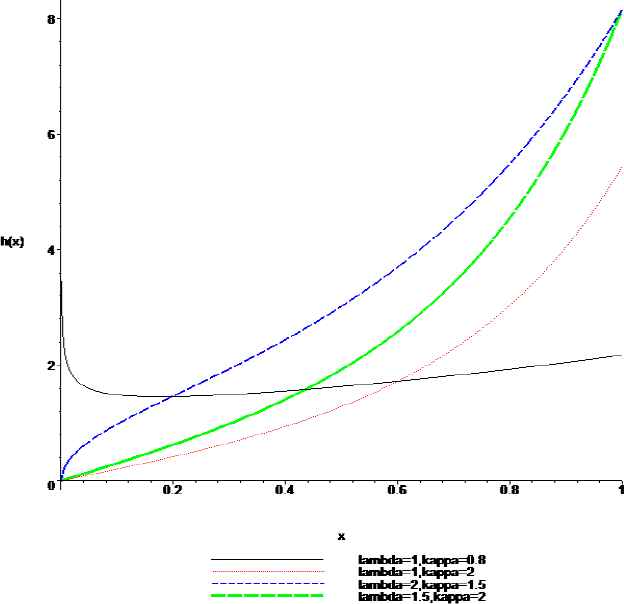
Hazard rate function, h(x), when X ~ chenexponentialpower (λ, κ).
The nth moment, E(Xn), where n > 0 is an integer, is given by
Letting u = − t in (2.5), and simplifying, we have
It is obvious from (2.6) that the 1st moment, E(X), is mathematically easily tractable for k = 1. So, by taking n = 1, k = 1 in (2.6), using Gradshteyn and Ryzhik [10], Eq. 4.337.2, Page 574, and simplifying, we have
For a detailed treatment of properties of Chen’s two-parameter exponential power life-testing distribution, we refer the interested readers to Chen [5].
3. Characterization Results
In this section, we provide our proposed characterizations of Chen’s two-parameter exponential power life-testing distribution, with pdf (2.1) and cdf (2.2), by truncated moment. For this, we will need the following assumption and lemmas.
Assumption and Lemmas
Assumptions 3.1.
Suppose the random variable X is absolutely continuous with the cumulative distribution function F(x) and the probability density function f(x). We assume that ω = inf {x | F(x) > 0}, and δ = sup{x | F(x) < 1}. We also assume that f(x) is a differentiable for all x, and E(X) exists.
Lemma 3.1.
Under the Assumption 3.1, if E(X|X ≤ x) = g(x)τ(x), where
Proof.
Suppose that E(X|X ≤ x) = g(x)τ(x). Then, since
Differentiating both sides of the above equation with respect to x, we obtain
From the above equation, we obtain
On integrating the above equation with respect to x, we have
Lemma 3.2.
Under the Assumption 3.1, if
Proof.
Suppose that
Differentiating the above equation with respect to respect to x, we obtain
From the above equation, we obtain
On integrating the above equation with respect to x, we have
where c is obtained by the condition
Theorem 3.1.
If the random variable X satisfies the Assumption 3.1 with ω = 0 and δ = ∞, then
Proof.
Suppose that
Conversely, suppose that
Then, using Lemma 3.1, differentiating g(x) with respect to x, and simplifying, we have
Since, by Lemma 3.1, we have
On integrating the above expression with respect to x and simplifying, we obtain
Theorem 3.2.
If the random variable X satisfies the Assumption 3.1 with ω = 0 and δ = ∞, then
Proof.
Suppose that
Conversely, suppose that
Then, using Lemma 3.2, differentiating
Since, by Lemma 3.2, we have
4. Conclusion
In this paper, we have considered the two-parameter exponential power life-testing distribution introduced by Chen [5], and provided its characterizations by truncated moment method. We hope the findings of the paper will be quite useful for the practitioners in various fields of sciences.
ACKNOWLEDGEMENT
Authors are thankful to the referees and editor-in-chief of the journal for their valuable comments and suggestions, which improved the presentation of this paper greatly. The first author, M. Shakil, is grateful to Miami Dade College for giving him the opportunity to be of service to this institution, without which it would have been impossible to conduct his research. Also, this article was partially completed while the third author, B. M. Golam Kibria, was on sabbatical leave (Fall 2017). He is grateful to Florida International University for awarding him the sabbatical leave which gave him excellent research facilities.
Footnotes
References
Cite this article
TY - JOUR AU - M. Shakil AU - M. Ahsanullah AU - B. M. Golam Kibria PY - 2018 DA - 2018/09/30 TI - On the Characterizations of Chen’s Two-Parameter Exponential Power Life-Testing Distribution JO - Journal of Statistical Theory and Applications SP - 393 EP - 407 VL - 17 IS - 3 SN - 2214-1766 UR - https://doi.org/10.2991/jsta.2018.17.3.1 DO - 10.2991/jsta.2018.17.3.1 ID - Shakil2018 ER -
