Optimality, cost minimization and the design of arterial networks

Alun D. Hughes

doi:10.1016/j.artres.2015.01.001

Download article (PDF)

Next Article In Issue>

Volume 10, Issue C, June 2015, Pages 1 - 10

Optimality, cost minimization and the design of arterial networks

Authors

Alun D. Hughes

Institute of Cardiovascular Sciences, University College London, London, WC1E 6BT, UK

E-mail address: alun.hughes@ucl.ac.uk.

Received 7 January 2015, Accepted 12 January 2015, Available Online 24 February 2015.

DOI: 10.1016/j.artres.2015.01.001 How to use a DOI?
Keywords: Circulation; Design; Optimality; Shear stress
Abstract: The arterial circulation acts as a network to deliver nutrients and oxygen to cells. The design of the cardiovascular system is subject to a variety of constraints and costs. It has been postulated that the design of the arterial network might be understood in terms of the need to minimize competing ‘costs’ within the context of physical or material limits to the system. These designs can also be envisaged as being subservient to space filling or fractal considerations. The signalling mechanisms underlying these designs remain to be fully characterized although shear stress, wall tensile stress and metabolic stimuli are likely candidates. I will also review evidence that deviations from a minimal cost condition or optimal design may provide both a measure of disease severity and insights into the underlying disease mechanism.
Copyright: © 2015 Association for Research into Arterial Structure and Physiology. Published by Elsevier B.V. All rights reserved.
Open Access: This is an open access article distributed under the CC BY-NC license.

Introduction

In branching cones the living web expands^a

Lymphatic ducts, and convoluted glands;

Aortal tubes propel the nascent blood,

And lengthening veins absorb the refluent flood;

The aim of this paper is to review ideas regarding the design of arterial networks in relation to optimal design and cost minimization. I will also discuss some evidence that disease is associated with deviations from an ‘optimal’ design. I will not review the genetic, epigenetic, or signalling mechanisms putatively involved in establishing and maintaining optimal design or issues related to optimal coupling of the heart and vascular system. For these topics readers are referred to other articles.^1–6

Design of arterial networks

The idea that morphology and function are causally interrelated can be traced back at least to Hellenistic philosophy^7,8; however attempts to make quantitative links between morphological design and function based on mechanistic arguments or analysis emerged in the Enlightenment, following the work of Galileo, Borelli, Newton and Harvey.⁹

In 1515 Leornardo da Vinci described tree boughs as preserving cross-sectional area at branches^b, but as far as I know the first attempt to quantify relationships between blood vessels at bifurcations in an arterial network was made by James Keill in 1708. Keill made anatomical measurements of arteries from dog, calf and man with the aim of calculating ‘the Quantity of Blood in the Humane Body’. He found that the ratio of vessel cross-sectional areas at a bifurcation was typically 41616:52126^c (i.e. 1: 1.25) and used this ratio in combination with geometric scaling laws to give crude estimates of total blood volume and blood flow velocity in capillaries. Woldenberg¹⁰ has provided a detailed critical description of Keill’s work on the arterial network, and his relationship to the English ‘iatromechanists’,^d and to other scientists, such as Hales and Young. Young refers to Keill’s data in his 1808 Croonian Lecture¹¹ where he assumes a consistent increase in area of 1:1.26 at each arterial bifurcation. Young makes no comment on the possible significance of this relationship (1:2^1/3), although it seems unlikely that it could have escaped his notice.¹² Roux, in his doctoral thesis later in the 19th century, undertook a detailed study of the relationships between diameters and the angles subtended by arteries at bifurcations.¹³ He concluded that ‘the shape and direction of the lumen of the blood vessels at their branch points is mainly determined by the action of hydrodynamic forces’. Roux is probably best known the founder of the Entwick-lungsmechanik^e, a ‘Kantian Mechanist’ programme for embryology and development.¹⁴ Roux envisaged that development was shaped by the interaction between forces and ‘Darwinian’ selection within an organism operating at a cellular level.¹⁵ Roux’s views were very influential in the late 19th and early 20th century and contributed to a greater integration of physics and mathematics into biological analysis.¹⁶ In 1901 Richard Thoma¹⁷ proposed that the size of arteries depended on the velocity of blood flow in the vessel. He proposed that the diameters between parent and offspring branches conformed to an exponential relationship

r0x=r1x+r2x

where r₀, r₁ and r₂ are the radii of the parent, and offspring branches at a bifurcation and x is the branching exponent (also termed the bifurcation or junction exponent). Based on measurements in chick embryo and human aorta he suggested that x fell between 2.5 and 3, with values being closer to x = 3 in early embryonic life. In 1903 Hess¹⁸ extended Roux’s work on branching and suggested that a typical branching angle of around 70° could be explained by minimization of energy losses; stating that ‘the most favourable branch angle is the angle whose cosine is equal to the ratio of the energy loss the blood undergoes in the parent vessel compared to a branch of the same length’. Thompson¹⁹ referred to both Roux’s and Hess’ work and reproduced Hess’ diagrams and calculations in the first edition of his classic work ‘On Growth and Form’ published in 1917. Ultimately the most influential studies of this era were those of Murray who published three articles^20–22 that are now widely viewed as the seminal early works on optimality principles in vascular design and gave rise to the eponymous ‘Murray’s Law’.

In the first pair of papers^20,21 Murray aimed to find physical laws that described the organization of the vascular system in relation to oxygen transport and exchange at the capillary level. He envisaged this as ‘a problem of maxima and minima’ and employed the idea of two competing economic factors: the cost of blood flow (i.e. power^f expended) and the cost of the blood volume. Using an assumption of Poiseuille flow and that the cost of the blood volume per unit length was proportional to the area of the vessel, Murray calculated that for maximal efficiency (in terms of blood flow and volume) blood flow should be proportional to the cube of the radius of the vessel, r, hence for a bifurcating network minimization of cost would be achieved if

r03=r13+r23

where 0, 1 and 2 denote parent and offspring branches respectively. Murray demonstrates that this gives reasonably plausible estimates of blood flow in small blood vessels; however he notes that this simple model does not hold for the aorta and ascribes this to the pulsatile nature of flow in this artery. In a third paper²² Murray extended his analysis to look at the angles subtended by branches with respect to the axis of the parent. Using the optimality arguments developed in his earlier paper he calculated that the optimal angle subtended by the major and minor branches should (θ₁ and θ₂ respectively)

cos θn=r04+ri4−(r03−ri3)432r02ri2

or for the combination of these angles (θ₁ + θ₂) – the branching angle

cos(θ1+θ2)=(r13+r23)43−r14−r242r12r22

Murray commented that Hess had neglected the conditions in the other branch (or continuing segment of the parent artery) on his analysis and that his conclusion was therefore incorrect.

Another comprehensive treatment based on the minimum energy principle was undertaken by Cohn^23,24 in 1954. Cohn argued that four factors should be optimised: 1) the size of the aorta; 2) capillary dimensions and the volume of tissue supplied by a capillary; 3) the connecting system between the aorta and the capillaries, and 4) the total resistance of the system to flow. The size of the aorta was considered to be constrained by the need to avoid turbulence; the capillary dimensions and capillary density were determined by diffusional considerations and the size of the erythrocyte; while the connecting network was considered to be constructed to optimise space filling while minimising resistance. For simplicity, Cohn assumed that branches were symmetrical and minimized resistance on the basis of Poiseuille flow. He also assumed that the mass of the blood vessel wall was determined by Laplace’s relationship for wall tension. Cohn then derived an ‘optimal’ relationship of

ri=2−i3r1

where r_i is the radius of the i^th offspring of the parent vessel with radius, r₀. This result is the same as Murray’s when applied to symmetrical bifurcations (Cohn appears to have been unaware of Murray’s papers). Cohn also used a space-filling argument to model the length of the offspring vessels which he predicted should conform to the relationship

li=l0/2i3

where l_i is the length of the i^th offspring of the parent vessel with length, l₁. Cohn compared his predictions with measurements of the aortic radius, the ratio of parent to offspring diameter, total blood flow and number of generations of branches in dog and found reasonable agreement.

Taylor²⁵ developed Cohn’s arguments and applied them to pulsatile flow in elastic arteries in a rarely cited^g but interesting paper. Taylor accepted the assumptions of minimum energy expenditure in terms of blood flow and blood volume but also argued that it would too costly in terms of cardiac work to allow the small arterial terminations to be impedance matched to the proximal conducting elastic arteries; hence reflections were inevitable. Essentially this constraint appears to be an extension of the minimum volume argument, although Taylor does not make it explicit. Taylor further assumed that optimality considerations required global impedance (the complex ratio of pressure to flow rate) to be stable over a range of frequencies and minimized. He drew two interesting and important conclusions from his analysis: 1) that if the distance to the “average reflecting site” of the scattered terminations were greater than the quarter wavelength of the fundamental harmonic then out of phase reflections from terminations would tend to cancel out and 2) if the wave speed of the network increased progressively outward along the paths connecting the heart to the terminations this would tend to ‘uncouple’ the termination and minimise the impact of reflections. Taylor concluded that the branched anatomical design of the arterial network allowed the heart to ‘see’ the proximal distensible region while keeping the overall compliance of the system low and minimizing the influence of reflections on the heart. Although not couched in these terms Taylor described a system that from the heart’s perspective looks like a ‘Windkessel’ despite the presence of reflected waves. More recently Parker et al.²⁶ have used an analogous power minimization argument to propose that reservoir pressure, which roughly equates to Windkessel pressure, represents a minimum power condition for the circulation and that the difference between total and reservoir pressure (excess pressure) might be used as an indicator of non-optimal circulatory performance. Consistent with this suggestion excess pressure has been reported to predict cardiovascular events independent of conventional risk factors.²⁷

Zamir²⁸ recognised that the optimality approaches outlined above lacked any plausible mechanism by which global optimality could be implemented. In other words how could a single bifurcation sense what was going on in billions of other bifurcations or the total volume of blood in the system? Zamir²⁹ noted that under conditions of Poiseuille flow the shear stress, τ, was given by

τ=4ηQπr3

where η is viscosity and Q is flow rate; hence there would be constant shear stress throughout a bifurcating network conforming to Murray’s law. Given the known sensitivity of endothelial cells to shear stress and other work suggesting that shear stress influenced vascular calibre,³⁰ Zamir therefore proposed that shear stress acting on endothelial cells might prove to be the major mechanism maintaining blood vessel diameter around the Murray optimum. In other papers,^28,31 Zamir described a range of possible optimality principles for arterial bifurcations (minimal lumen surface area, minimal volume, minimal power and minimal drag) in terms of the angle subtended by both branches (the branching angle) and the ratio of parent to offspring areas (β) and showed that if they conformed with Murray’s law, surface area, volume, pumping power and the drag force would all be close to their respective minima if the bifurcation angle was within the range 75–100°. Uylings³² extended previous work to accommodate all types of steady flow including completely turbulent flow, non-cylindrical vessels and asymmetrical branches and employed a general flow relation that minimized power losses:

Q=krj+2j−2

where j = 4.0 for laminar flow, j = 5.0 for turbulent flow and k is a constant. On this basis he calculated that the optimal branching exponents would range from 2.33 to 3.0 for completely turbulent to laminar flow respectively. He also calculated that the optimal junction exponents would range between the limits of 2 (unbranched vessel) to 3 (symmetrically branched vessel) with increasing branching symmetry assuming laminar flow. Roy and Woldenberg³³ and proposed a generalized model of optimal branching geometry that allowed relationships between angles and branching asymmetry to be determined for a range of junction exponents. This permitted the application of the approach to a wide range of biological and non-biological branching structures.

In 1981 Sherman¹² published an influential review that summarized much of the work up to that time and examined the extent to which Murray’s law fitted experimental data. He concluded that the fit was good, although not perfect, and he made some important points: 1) Murray’s law might apply to inanimate systems if a trade-off between power and volume were made at some point during construction or development; 2) Murray’s law would only apply to systems where flow conductance was proportional to r⁴ (i.e. Poiseuille flow); 3) changes in diameter would have to be coordinated across a large region in response to dynamic change.

Subsequent authors addressed the impact of turbulence³⁴ and viscosity across the network^34,35. Several studies looked at the predicted costs associated with deviation from optimality.^34,36–38 These studies showed relatively shallow cost functions for small deviations from optimal which became much steeper with large deviations. In general the observed deviations seen in experimental data incurred costs that were small (<10%). Taken together these studies and others (reviewed in ³⁹) provided fairly substantial broad support for Murray’s law in a range of fluid conducting systems where Poiseuille flow was present and these data were consistent with a role for shear stress in maintaining this relationship.

West et al.⁴⁰ dealt with large arteries in an important but controversial^41–43 paper on allometric scaling. They proposed that the branch exponent for large elastic arteries with pulsatile flow should be 2 (area preserving) and that there should be a rather abrupt ‘step-like’ transition to the area-increasing (shear-preserving) relationship predicted by Murray in smaller arteries. It was assumed that branching followed a fractal-like space filling paradigm (see below) and that capillaries were size-invariant units. Womersley’s linearized solution to the Navier–Stokes equations was used with the assumption of a thin wall and incompressible fluid. Under these assumptions the impedance, Z is given by

Z≈c02ρπr2c

where c₀ is the Moens-Korteweg wave speed, ρ is density and

(cc0)2≈J2(i3/2α)J0(i3/2α)

where J_n denotes the Bessel function of order n, and α is a dimensionless parameter known as the Womersley number. This model agrees better with experimental data,⁴⁴ although some of the assumptions and its implications for allometric scaling have been criticised.^41,42,45,46 Savage et al.,⁴⁶ while critical of the West model in some respects, used a broadly similar approach to estimate that the transition from x = 2 to x = 3 might be expected to occur over arteries with diameters between 1 cm and 0.1 cm. Huo and Kassab^47,48 formulated a scaling law for vascular trees that related cumulative vessel volume, length and diameter in arterial trees. This approach built on the approach used by West et al. but derived volume–diameter and flow–length scaling laws from conservation of mass without invoking the more controversial space-filling assumptions. Huo and Kassab considered the arterial tree as composed of multiple stem-crown units (Fig. 1) and excluded capillaries since they were not considered tree-like structures.⁴⁹ They derived volume–diameter, flow–length, diameter–length, flow–diameter and flow–volume scaling laws and showed good agreement with experimental data.⁴⁸ The estimated branching exponent varied with vessel size, being on average ∼3 in small arteries and arterioles, ∼2.3 in large arteries and ∼2.6 averaged over all trees studied.⁴⁸

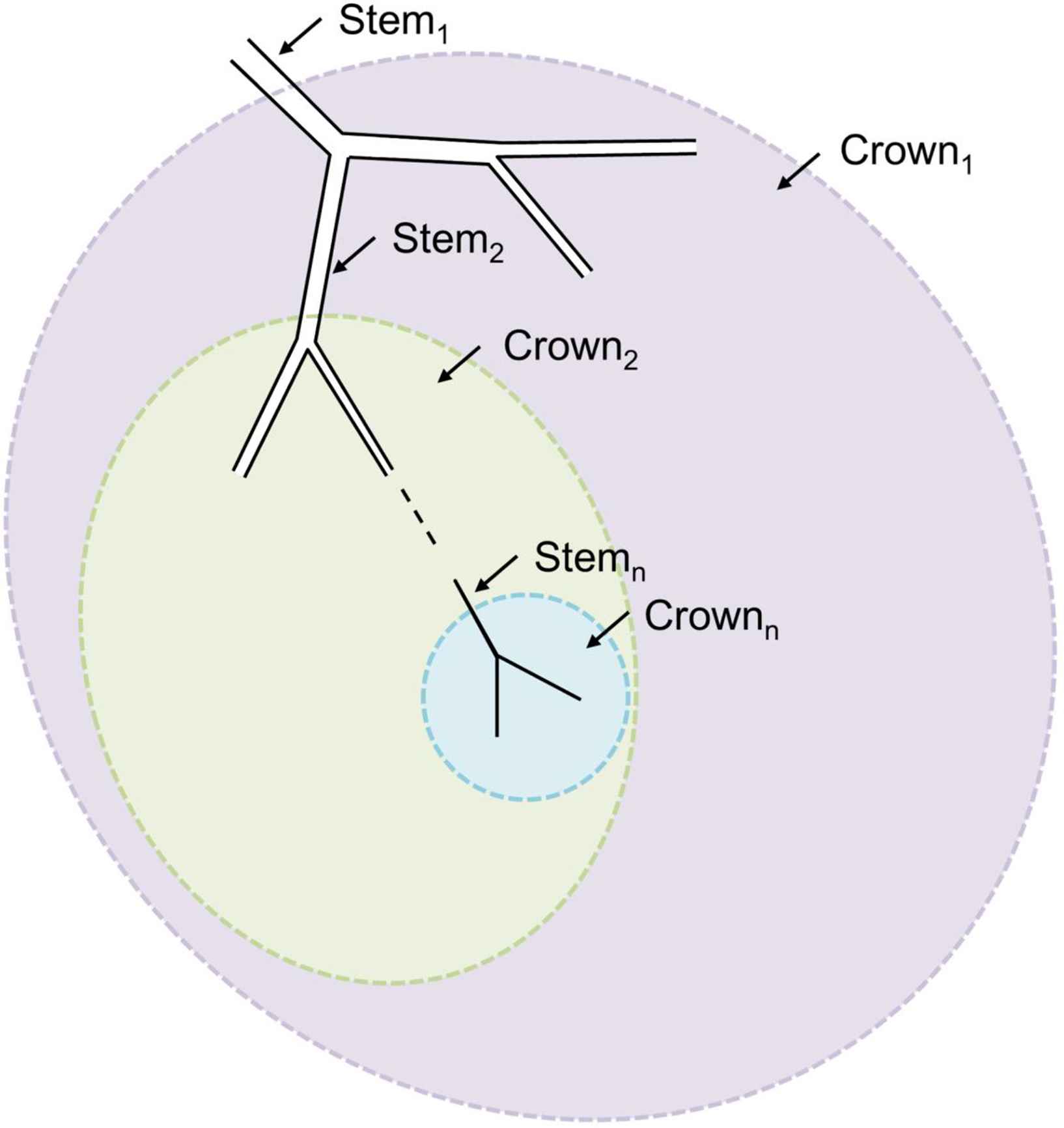
Mechanisms of optimality

Sherman¹² had considered that coordination of network behaviour would be difficult to achieve following dynamic change in a network of arteries. Griffith and colleagues^50,51 however provided experimental evidence of a mechanism that could account for this. They used perfused rabbit ears with five generations of branches (G0 to G4) visualised by microangiography. They showed that flow-dependent release of endothelium derived relaxing factor (EDRF; probably nitric oxide (NO) in this experimental system) maintained diameters of different generations of resistance arteries close to Murray’s predicted optimum, either under resting conditions with myogenic tone, or following vasoconstriction with serotonin.^50,51 When EDRF was inhibited with haemoglobin, branching exponents deviated markedly from 3 with the average junction exponent being ∼6 in the presence of serotonin. Similar findings were made in the human retina under resting conditions in vivo when NO synthase was inhibited by NG-monomethyl-l-arginine (L-NMMA).⁵² These experimental findings are consistent with Zamir’s original proposal that shear stress is a key influence on arterial network design, at least in arteries that experience Poiseuille flow. However the idea that microvascular networks could be understood solely in terms of a feedback-model mediated by endothelial shear stress has been criticised by several authors and they emphasize that other factors influence arterial structure (e.g. pressure, oxygen tension, and metabolic factors).^53–55 Several models incorporating the effects of pressure, smooth muscle tone, non-Newtonian rheology and metabolism have been formulated.^56–59 Pries and Secomb recently proposed a sophisticated model to describe microvascular remodelling.⁶⁰ They did not discount an important role for shear stress and the endothelium in the coordination and design of arterial networks but their model also incorporated the effects of circumferential wall stress, metabolic factors and conducted responses as important influences in network design and remodelling (Fig. 2).

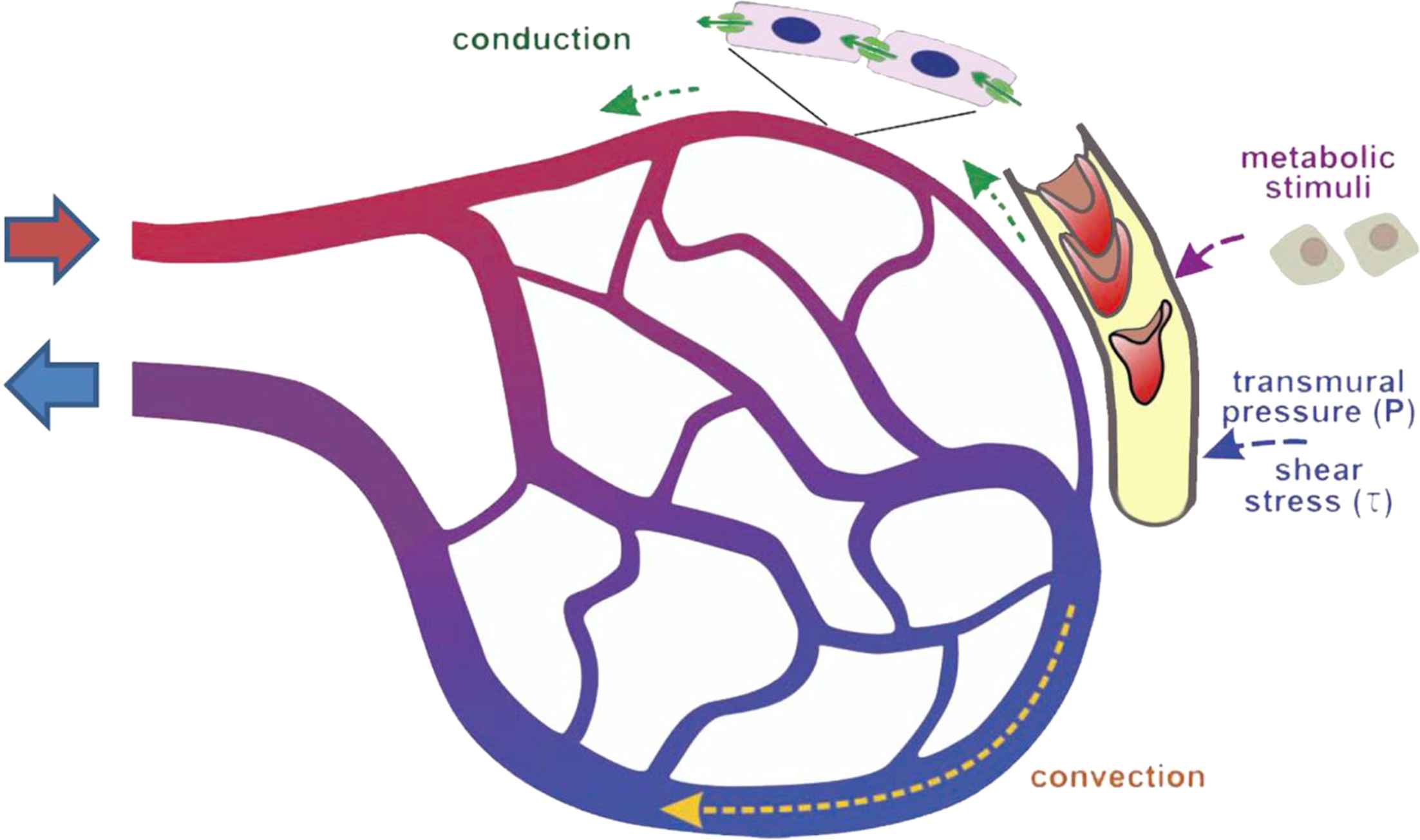
The mechanisms that might account for the closer adherence of large elastic arteries to an area-preserving branch exponent (x ∼ 2) are less well understood. However, one might speculate that limited access of NO and other endothelium-derived mediators into the arterial wall,⁶¹ wall circumferential stress⁶² and/or the effects of flow separation and complex flow⁶³ could be important factors.

Fractals

Fractals were first applied to arterial design in the 1980’s. At first sight fractal analysis appears to differ from cost-effectiveness analysis, although in fact the two can be linked through scaling considerations.^40,64 The term fractal was coined by Mandelbrot to describe self-similar structures with a fractional (non-unity) dimension and devoted some discussion to vascular networks in his classic book, ‘The Fractal Geometry of Nature’.⁶⁵ Vascular networks are not strictly fractal as they do not exhibit scale invariance over an infinite range of scales,⁶⁶ but they show sufficient self-similarity to be treated as fractal or pseudo-fractal. The fractal dimension (Hausdorff-Besicovitch dimension) is widely used as a measure of statistical self-similarity across scaling levels and can be viewed as a measure of the effectiveness of space filling. Thus for a two-dimensional branching network (e.g. the retinal vasculature) the upper limit of the fractal dimension should be the topological dimension (i.e. 2 since a flat surface is 2 dimensional) – the closer the fractal dimension is to 2 the better the space filling. Typically the fractal dimension of healthy 2-dimensional (or 3 dimensional vascular networks analysed as a 2-dimensional slice) falls within the range 1.3–2.0.⁶⁷ Fractal dimension can be viewed as complementary to older measures of vessel density⁶⁸; both approaches quantify space filling, but they do not necessarily correlate closely because differences in vessel diameter affect conventional measures of density.⁶⁹ Lacunarity is another measure that may be useful in describing fractal or quasi-fractal structures. Lacunarity quantifies the distribution of gap size, or lacunae, in the structure. Objects with similar fractal dimensions, may differ by lacunarity; however, as yet, lacunarity has seen only limited application to vascular networks.^69–71

Takahashi⁷² formulated an explicit link between the fractal dimension and Murray’s law by assuming that capillaries are of uniform size and that relationship between vessel radius and length can be described by an allometric function:

l(r)=βrα

where the length exponent, α and the length coefficient, β are constants; this is consistent with fractal recursion, i.e. the branching structure is self-similar although scale differs.⁷³

Under these assumptions Takahashi shows that:

(rtr0)−(D+α)=(rtr1)−(D+α)+(rtr2)−(D+α)

where r_t is the radius of the terminal vessel (or capillary) and D is the fractal dimension. So dividing throughout by r_t and taking the reciprocal

r0(D+α)=r1(D+α)+r2(D+α)

This is similar in form to Murray’s law and the branching exponent, x would be expected to be equal to D + α. Takahashi predicted that D + α should be 2.88 and observed that this was consistent with literature values for the branching exponent. Morphological studies indicate that the value of α is on average close to unity (0.76–1.21) in healthy vasculature.⁷² This also provides a rationale for using length to diameter ratio as a scale-independent normalization of retinal vessel structure.⁷⁴ Fractal dimensions in the vasculatures range between 1.1 and 2.0,⁶⁷ so one would expect x to range between ∼2 and 3 by this argument. Consistent with Takeda’s suggestion lower branch exponents were associated with lower arteriolar microvascular density in the retinal arteriolar network.⁷⁵ More recently vascular networks have been treated as multifractal networks^67,76 i.e. networks that show heterogeneity in scaling at different levels or regions of the network. Other approaches that have been applied to arterial networks include graph theory⁷⁷ and network topological measures.⁷⁸

Departures from optimal design in disease

If the normal network of small arteries is close to Murray’s optimum then it seems plausible that disease may disturb that relationship. Hutchins et al. visualised post mortem coronary arteries using an angiographic technique.⁷⁹ They reported that in normal left main coronary arteries from 107 hearts the branching exponent was close to 3 (average x = 3.2) consistent with Murray’s law, but declined progressively with more severe coronary artery disease with average x = 2.2 in 17 hearts with grade 3 or 4 atherosclerosis. However the resolution of their measurements was limited to 0.1 mm and extensive characterisation of the tree could not be achieved due to the limitations of the angiographic approach. More recent work in 253 patients undergoing coronary artery intravascular ultrasound reported that deviation from Murray’s law was associated with increased coronary artery calcification.⁸⁰ In pigs Zhang and Kassab reported that hypertension and LV hypertrophy was not associated with departure of coronary artery branching exponents from 3.⁸¹

The retinal circulation offers an excellent opportunity to assess branch exponents and microvascular architecture non-invasively in man.⁸² In a small study, Stanton et al.⁷⁵ examined retinal arterioles using fluorescein angiography and reported that branch exponents were similar for normotensives (mean x = 2.7) and hypertensive individuals (mean x = 2.5), but that increased age was associated with branch exponents <3. Bifurcation angles were more acute in hypertensives (74°) than in normotensives (84°) and declined with increasing age in both groups. Chapman et al. reported that the branch exponents measured from retinal arterioles in healthy men were close to optimal (mean x = 3.1), but were significantly reduced (mean x = 2.6) in men with atherosclerosis and peripheral vascular disease.⁸³ Witt et al. subsequently reported that increased deviation from an ‘optimal’ branch exponent of x = 3 was associated with increased future risk of coronary heart disease in an analysis of retinal photographs from the Beaver Dam Eye study.⁸⁴ Another study in stroke patients also found average area ratios at branches exceeded the optimal value predicted by Murray’s Law and that more deviation from optimal was associated with ischaemic heart disease and increased periventricular white matter hyperintensities.⁸⁵ Patton et al. reported that non-optimal branching of retinal arteries associated with impaired general cognitive ability and verbal fluency, whereas non-optimal branching angles were associated with reduced logical memory.⁸⁶ Tillin et al. found that African-Caribbean people had less optimal retinal arteriolar branching exponents compared with Europeans⁸⁷; this was suggested to be relevant to the greater risk of stroke⁸⁸ and the more adverse cerebrovascular impact of high blood pressure⁸⁹ in this ethnic group. Greater deviation of the branch exponent (from 3) in arteries has also been reported to be associated with proliferative retinopathy⁹⁰ and peripheral neuropathy⁹¹ in adults with type 2 diabetes. Longer duration of Type 1 diabetes was also associated with an increased optimality deviation.⁹²

Non-optimal branching geometry has also been observed in relation to adverse risk factors in early life.⁸² Low birth weight, a risk factor for cardiometabolic disease in adult life was associated with increased deviation of branching exponents from optimal values in children aged 11.⁹³ Offspring of hypertensive parents (aged 9–14 y) have also been reported to have greater deviation of branch exponents from Murray’s optimal value.⁹⁴

Fractal dimension has been used quite extensively to assess vascular networks in cardiometabolic and other diseases. Both reduced and increased fractal dimension has been seen in several conditions that affect the circulation (Table 1) and interpreted as indicative of a suboptimal circulatory network. Null associations have also been observed. There is some limited information regarding the relationship of fractal measures with outcomes. Low fractal dimension of the pulmonary arterial tree on CT angiography predicted poorer survival in one prospective study of people with pulmonary hypertension,⁹⁵ and low fractal dimension has also been associated with an increased risk of stroke.⁹⁶ Being in the higher or lower quarter of fractal dimension was associated with an increased risk of coronary heart disease mortality.⁹⁷ Greater retinal fractal dimension was independently associated with early retinopathy in a study of young people (aged 12–20 y) with type 1 diabetes,⁹⁸ but fractal dimension was not reported to be associated with incident retinopathy in another study of children and adolescents with type 1 diabetes.⁹⁹ In older adults with type 1 diabetes a lower retinal fractal dimension was associated with complications, including proliferative retinopathy, neuropathy and older age, but not macrovascular disease.^100,101

Conclusions

Application of a cost minimization approach has proved useful in the analysis of arterial networks, although it is not without limitations and a number of issues remain unresolved. Although progress has been made we need to know more about the stimuli which shape the network, how their effects are mediated, and to what extent they synergise. There is some evidence that shear stress and pressure interact,⁵⁵ and a range of interactions between diverse stimuli might permit a degree of ‘weighting’ or contextualization. For instance, it has been argued the circulation might be designed to attain highest efficiency during exercise,^44,102 and by implication that it is slightly suboptimal under resting conditions – effectively allowing a reserve capacity. This is consistent with some evidence, at least in terms of minimization of wave reflection.¹⁰³ If this were true, the system would need to optimize its design in response to an intermittent physiological state, albeit one that may be critical for survival. How is this intermittent state sensed? One possibility might be that shear stress could have more effect on remodelling in the context of the stimuli that accompany exercise.

Circulation	Disease/Condition	Summary of findings	Comments	References
Retinal	Hypertension/High BP	Lower D_f	Arteries and veins not distinguished	^105–110
	Ischemic stroke	Lower D_f	Both arteries and veins	¹¹¹
	CADASIL	Lower D_f	Arteries and veins not distinguished	¹¹²
	Type 1 or Type 2 Diabetes	Inconsistent	Arteries and veins not distinguished	^113–120
	Cognitive dysfunction	Lower D_f	Arteries and veins not distinguished	¹²¹
	Alzheimer’s disease	Lower D_f	Both arteries and veins	¹²²
	Human immunodeficiency virus (HIV) infection	D_f not different	Arteries and veins not distinguished	¹²³
	Obesity	D_f not different	Arteries and veins not distinguished	¹²⁴
	Glaucoma	Lower D_f	Arteries and veins not distinguished	¹²⁵
	Renal dysfunction/CKD	Lower D_f		^126,127
Renal	Congenitally abnormal kidneys	Lower D_f	Only 2 abnormal kidneys examined	¹²⁸
Pulmonary	Pulmonary Hypertension	Inconsistent		^129–131

Table 1

Vascular fractal measures in cardiometabolic and other diseases. Abbreviations: CADASIL – Cerebral Autosomal Dominant Arteriopathy with Subcortical Infarcts and Leukoencephalopathy; CKD – chronic kidney disease; D_f – fractal dimension.

Finally, is optimal design desirable? It has recently been proposed (for the bronchial tree) that an optimal network is dangerous because of its vulnerability to imperfections or vessel constriction and that a ‘safety margin’ is required in design.¹⁰⁴ This seems difficult to reconcile with the comparative cost-insensitivity of arterial networks to small deviations from optimum, but it does raise important questions about the appropriateness of optimality as an overriding factor in circulatory design – perhaps Murray’s law should be viewed as ‘more what you’d call guidelines than actual rules.’^h

Funding

AH has received financial support from the British Heart Foundation (PG/12/29/29497) and the National Institute for Health Research, University College London Hospitals Biomedical Research Centre relating to this research.

Conflicts of interest

None.

Acknowledgements

I am grateful to Nish Chaturvedi for critical reading of this paper.

Footnotes

a

From The Temple of Nature: Or the Origin of Society: A Poem with Philosophical Notes (1803) by Erasum Darwin. (Darwin’s notes) In branching cones, l. 259. The whole branch of an artery or vein may be considered as a cone, though each distinct division of it is a cylinder. It is probable that the amount of the areas of all the small branches from one trunk may equal that of the trunk, otherwise the velocity of the blood would be greater in some parts than in others, which probably only exists when a part is compressed or inflamed.

b

“Every year when the boughs of a tree have made an end of maturing their growth, they will have made, when put together, a thickness equal to that of the main stem.” Leonardo da Vinci (1515).

c

Keill is vague on units but Woldenberg (Woldenberg MJ. James Keill (1708) and the morphometry of the microcosm. Geometric progression laws in arterial trees. In: Stoddart DR, ed. Process and form in geomorphology. London; New York: Routledge; 1997) suggests that these are square inches.

d

For further information on the iatromechanists in 17th century see Brown, T. M (1970). The College of Physicians and the acceptance of iatromechanism in England, 1665–1695 Bulletin of the History of Medicine, 44(1), 12–30.

e

Literally translated as ‘Developmental Mechanics’; however Roux had a more causal perspective than this translation might imply.

f

Murray terms this factor work, but as Zamir (Zamir M. Optimality principles in arterial branching. J Theor Biol. 1976; 62:227–251) points out he is really describing power.

g

Taylor’s paper has been cited twice since its publication in 1967 according to Scopus (accessed 10/09/2014).

h

Line from Pirates of the Caribbean: The Curse of the Black Pearl (2003).

References

1.PD Chantler and EG Lakatta, Arterial-ventricular coupling with aging and disease, Front Phys, Vol. 3, 2012, pp. 90.

2.EA Jones, F le Noble, and A Eichmann, What determines blood vessel structure? Genetic prespecification vs. hemodynamics, Physiol (Bethesda, Md.), Vol. 21, 2006, pp. 388-95.

3.D Liu, J Krueger, and F Le Noble, The role of blood flow and micrornas in blood vessel development, Int J Dev Biol, Vol. 55, 2011, pp. 419-29.

4.MC van Oostrom, O van Oostrom, PH Quax, MC Verhaar, and IE Hoefer, Insights into mechanisms behind arteriogenesis: what does the future hold?, J Leukoc Biol, Vol. 84, 2008, pp. 1379-91.

5.B Larrivee, C Freitas, S Suchting, I Brunet, and A Eichmann, Guidance of vascular development: lessons from the nervous system, Circ Res, Vol. 104, 2009, pp. 428-41.

6.CP Chang and BG Bruneau, Epigenetics and cardiovascular development, Annu Rev Phys, Vol. 74, 2012, pp. 41-68.

7.H Von Staden, Teleology and mechanism in aristotelian biology and early hellenistic medicine Aristotelische biologie : Intentionen, methoden, ergebnisse, W Kullmann (editor), F. Steiner Verlag, Stuttgart, 1997, pp. 193-208.

8.R Rosen, Optimality principles in biology, Butterworths, London, 1967.

9.B Gunther, Dimensional analysis and theory of biological similarity, Phys Rev, Vol. 55, 1975, pp. 659-99.

10.MJ Woldenberg, James Keill (1708) and the morphometry of the microcosm. Geometric progression laws in arterial trees Process and form in geomorphology, DR Stoddart (editor), Routledge, London; New York, 1997.

11.T Young, The Croonian lecture: on the functions of the heart and arteries, Phil Trans R Soc Lond, Vol. 99, 1809, pp. 1-31.

12.TF Sherman, On connecting large vessels to small. The meaning of murray’s law, J Gen Physiol, Vol. 78, 1981, pp. 431-53.

13.W Roux, Über die verzweigungen der blutgefässe: Eine morphologische studie, G. Fischer, Cambridge, 1878.

14.S Roth, Mathematics and biology: a kantian view on the history of pattern formation theory, Dev Genes Evol, Vol. 221, 2011, pp. 5-6.

15.H Kurz, K Sandau, and B Christ, On the bifurcation of blood vessels – Wilhelm Roux’s doctoral thesis (Jena 1878) – a seminal work for biophysical modelling in developmental biology, Ann Anat, Vol. 179, 1997, pp. 33-6.

16.K Sander, Wilhelm Roux and his programme for developmental biology, Landmarks Dev Biol, Vol. 1883–1924, 1997. Springer Berlin Heidelberg

17.R Thoma, Über den verzweigungsmodus der arterien, Archiv für Entwicklungsmechanik der Organismen, Vol. 12, 1901, pp. 352-413.

18.W Hess, Eine mechanisch bedingte gesetzmäßigkeit im bau des blutgefäßsystems, Archiv für Entwicklungsmechanik der Organismen, Vol. 16, 1903, pp. 632-41.

19.DW Thompson, On growth and form, University Press, 1917.

20.CD Murray, The physiological principle of minimum work: II. Oxygen exchange in capillaries, Proc Natl Acad Sci U S A, Vol. 12, 1926, pp. 299-304.

21.CD Murray, The physiological principle of minimum work: I. The vascular system and the cost of blood volume, Proc Natl Acad Sci U S A, Vol. 12, 1926, pp. 207-14.

22.CD Murray, The physiological principle of minimum work applied to the angle of branching of arteries, J Gen Physiol, Vol. 9, 1926, pp. 835-41.

23.DL Cohn, Optimal systems: I. The vascular system, Bull Math Biophys, Vol. 16, 1954, pp. 59-74.

24.DL Cohn, Optimal systems: II. The vascular system, Bulletin Math Biophys, Vol. 17, 1955, pp. 219-27.

25.MG Taylor, The elastic properties of arteries in relation to the physiological functions of the arterial system, Gastroenterology, Vol. 52, 1967, pp. 358-63.

26.KH Parker, J Alastruey, and GB Stan, Arterial reservoir-excess pressure and ventricular work, Medical Biol Eng Comput, Vol. 50, 2012, pp. 419-24.

27.JE Davies, P Lacy, T Tillin, D Collier, JK Cruickshank, DP Francis, et al., Excess pressure integral predicts cardiovascular events independent of other risk factors in the conduit artery functional evaluation substudy of anglo-scandinavian cardiac outcomes trial, Hypertension, Vol. 64, 2014, pp. 60-8.

28.M Zamir, The role of shear forces in arterial branching, J Gen Phys, Vol. 67, 1976, pp. 213-22.

29.M Zamir, Shear forces and blood vessel radii in the cardiovascular system, J Gen Phys, Vol. 69, 1977, pp. 449-61.

30.S Rodbard, Vascular caliber, Cardiology, Vol. 60, 1975, pp. 4-49.

31.M Zamir, Nonsymmetrical bifurcations in arterial branching, J Gen Phys, Vol. 72, 1978, pp. 837-45.

32.HB Uylings, Optimization of diameters and bifurcation angles in lung and vascular tree structures, Bull Math Biol, Vol. 39, 1977, pp. 509-20.

33.AG Roy and MJ Woldenberg, A generalization of the optimal models of arterial branching, Bull Math Biol, Vol. 44, 1982, pp. 349-60.

34.MJ Woldenberg and K Horsfield, Relation of branching angles to optimality for four cost principles, J Theor Biol, Vol. 122, 1986, pp. 187-204.

35.A Kamiya, R Bukhari, and T Togawa, Adaptive regulation of wall shear stress optimizing vascular tree function, Bull Math Biol, Vol. 46, 1984, pp. 127-37.

36.TF Sherman, AS Popel, A Koller, and PC Johnson, The cost of departure from optimal radii in microvascular networks, J Theor Biol, Vol. 136, 1989, pp. 245-65.

37.M Zamir, Cost analysis of arterial branching in the cardiovascular systems of man and animals, J Theor Biol, Vol. 120, 1986, pp. 111-23.

38.M Zamir and DC Bigelow, Cost of departure from optimality in arterial branching, J Theor Biol, Vol. 109, 1984, pp. 401-9.

39.M LaBarbera, Principles of design of fluid transport systems in zoology, Science, Vol. 249, 1990, pp. 992-1000.

40.GB West, A general model for the origin of allometric scaling laws in biology, Science, Vol. 276, 1997, pp. 122-6.

41.J Kozlowski and M Konarzewski, Is West, Brown and Enquist’s model of allometric scaling mathematically correct and biologically relevant?, Funct Ecol, Vol. 18, 2004, pp. 283-9.

42.J Kozlowski and M Konarzewski, West, Brown and Enquist’s model of allometric scaling again: the same questions remain, Funct Ecol, Vol. 19, 2005, pp. 739-43.

43.PS Dodds, DH Rothman, and JS Weitz, Re-examination of the “3/4-law” of metabolism, J Theor Biol, Vol. 209, 2001, pp. 9-27.

44.RS Reneman and AP Hoeks, Wall shear stress as measured in vivo: consequences for the design of the arterial system, Med Biol Eng Comput, Vol. 46, 2008, pp. 499-507.

45.PR Painter, P Eden, and HU Bengtsson, Pulsatile blood flow, shear force, energy dissipation and murray’s law, Theor Biol Med Model, Vol. 3, 2006, pp. 31.

46.VM Savage, EJ Deeds, and W Fontana, Sizing up allometric scaling theory, PLoS Comput Biol, Vol. 4, 2008, pp. e1000171.

47.Y Huo and GS Kassab, A scaling law of vascular volume, Biophys J, Vol. 96, 2009, pp. 347-53.

48.Y Huo and GS Kassab, Intraspecific scaling laws of vascular trees, J R Soc Interface/R Soc, Vol. 9, 2012, pp. 190-200.

49.GS Kassab and YC Fung, Topology and dimensions of pig coronary capillary network, Am J Physiol, Vol. 267, 1994, pp. H319-325.

50.TM Griffith and DH Edwards, Basal EDRF activity helps to keep the geometrical configuration of arterial bifurcations close to the murray optimum, J Theor Biol, Vol. 146, 1990, pp. 545-73.

51.TM Griffith, DH Edwards, RL Davies, TJ Harrison, and KT Evans, Edrf coordinates the behaviour of vascular resistance vessels, Nature, Vol. 329, 1987, pp. 442-5.

52.NW Witt, N Chapman, SA Thom, AV Stanton, KH Parker, and AD Hughes, A novel measure to characterise optimality of diameter relationships at retinal vascular bifurcations, Artery Res, Vol. 4, 2010, pp. 75-80.

53.WJ Hacking, E VanBavel, and JA Spaan, Shear stress is not sufficient to control growth of vascular networks: a model study, Am J Physiol, Vol. 270, 1996, pp. H364-375.

54.AR Pries, TW Secomb, and P Gaehtgens, Design principles of vascular beds, Circulation Res, Vol. 77, 1995, pp. 1017-23.

55.ENTP Bakker, JP Versluis, P Sipkema, JWGE VanTeeffelen, TM Rolf, JAE Spaan, et al., Differential structural adaptation to haemodynamics along single rat cremaster arterioles, J Phys, Vol. 548, 2003, pp. 549-55.

56.R Revellin, F Rousset, D Baud, and J Bonjour, Extension of murray’s law using a non-newtonian model of blood flow, Theor Biol Med Model, Vol. 6, 2009, pp. 7.

57.LA Taber, An optimization principle for vascular radius including the effects of smooth muscle tone, Biophys J, Vol. 74, 1998, pp. 109-14.

58.MD Frame and IH Sarelius, Energy optimization and bifurcation angles in the microcirculation, Microvasc Res, Vol. 50, 1995, pp. 301-10.

59.Y Liu and GS Kassab, Vascular metabolic dissipation in Murray’s law, Am J Physiol Heart Circulatory Phys, Vol. 292, 2007, pp. H1336-1339.

60.AR Pries and TW Secomb, Modeling structural adaptation of microcirculation, Microcirculation, Vol. 15, 2008, pp. 753-64.

61.X Liu, P Srinivasan, E Collard, P Grajdeanu, JL Zweier, and A Friedman, Nitric oxide diffusion rate is reduced in the aortic wall, Biophys J, Vol. 94, 2008, pp. 1880-9.

62.MJ Mulvany, GL Baumbach, C Aalkjaer, AM Heagerty, N Korsgaard, EL Schiffrin, et al., Vascular remodeling, Hypertension, Vol. 28, 1996, pp. 505-6.

63.MJ Lighthill, Physiological fluid dynamics: a survey, J Fluid Mech, Vol. 52, 1972, pp. 475-97.

64.BJ West, Fractal physiology and chaos in medicine, World Scientific, Singapore; New Jersey, 1990.

65.BB Mandelbrot, The fractal geometry of nature, W.H. Freeman, San Francisco, 1982.

66.JG Restrepo, E Ott, and BR Hunt, Scale dependence of branching in arterial and bronchial trees, Phys Rev Lett, Vol. 96, 2006, pp. 128101.

67.S Lorthois and F Cassot, Fractal analysis of vascular networks: insights from morphogenesis, J Theor Biol, Vol. 262, 2010, pp. 614-33.

68.AV Stanton, P Mullaney, F Mee, ET O’Brien, and K O’Malley, A method of quantifying retinal microvascular alterations associated with blood pressure and age, J Hypertens, Vol. 13, 1995, pp. 41-8.

69.DJ Gould, TJ Vadakkan, RA Poche, and ME Dickinson, Multifractal and lacunarity analysis of microvascular morphology and remodeling, Microcirculation, Vol. 18, 2011, pp. 136-51.

70.G Landini, PI Murray, and GP Misson, Local connected fractal dimensions and lacunarity analyses of 60 degrees fluorescein angiograms, Invest Ophthalmol Vis Sci, Vol. 36, 1995, pp. 2749-55.

71.SC Cheng and YM Huang, A novel approach to diagnose diabetes based on the fractal characteristics of retinal images, IEEE Trans Information Technol Biomed, Vol. 7, 2003, pp. 163-70.

72.T Takahashi, Microcirculation in fractal branching networks, Tokyo: Springer Science & Business Media, New York, 2013.

73.JB Bassingthwaighte, LS Liebovitch, and BJ West, Fractal physiology, Oxford University Press, 1994.

74.LA King, AV Stanton, PS Sever, SA Thom, and AD Hughes, Arteriolar length-diameter (l:D) ratio: a geometric parameter of the retinal vasculature diagnostic of hypertension, J Hum Hypertens, Vol. 10, 1996, pp. 417-8.

75.AV Stanton, B Wasan, A Cerutti, S Ford, R Marsh, PS Sever, et al., Vascular network changes in the retina with age and hypertension, J Hypertens, Vol. 13, 1995, pp. 1724-8.

76.M Zamir, Fractal dimensions and multifractility in vascular branching, J Theor Biol, Vol. 212, 2001, pp. 183-90.

77.EM Wahl, LV Quintas, LL Lurie, and ML Gargano, A graph theory analysis of renal glomerular microvascular networks, Microvasc Res, Vol. 67, 2004, pp. 223-30.

78.AD Hughes, E Martinez-Perez, AS Jabbar, A Hassan, NW Witt, PD Mistry, et al., Quantification of topological changes in retinal vascular architecture in essential and malignant hypertension, J Hypertens, Vol. 24, 2006, pp. 889-94.

79.GM Hutchins, MM Miner, and JK Boitnott, Vessel caliber and branch-angle of human coronary artery branch-points, Circ Res, Vol. 38, 1976, pp. 572-6.

80.AW Schoenenberger, N Urbanek, S Toggweiler, R Seelos, P Jamshidi, TJ Resink, et al., Deviation from murray’s law is associated with a higher degree of calcification in coronary bifurcations, Atherosclerosis, Vol. 221, 2012, pp. 124-30.

81.GS Kassab and YC Fung, The pattern of coronary arteriolar bifurcations and the uniform shear hypothesis, Ann Biomed Eng, Vol. 23, 1995, pp. 13-20.

82.AD Hughes, Genetic and early life influences on the human retinal microcirculation, Basic & Clin Pharmacol Toxicol, Vol. 110, 2012, pp. 19-25.

83.N Chapman, G Dell’omo, MS Sartini, N Witt, A Hughes, S Thom, et al., Peripheral vascular disease is associated with abnormal arteriolar diameter relationships at bifurcations in the human retina, Clin Sci, Vol. 103, 2002, pp. 111-6.

84.N Witt, TY Wong, AD Hughes, N Chaturvedi, BE Klein, R Evans, et al., Abnormalities of retinal microvascular structure and risk of mortality from ischemic heart disease and stroke, Hypertension, Vol. 47, 2006, pp. 975-81.

85.FN Doubal, R de Haan, TJ MacGillivray, PE Cohn-Hokke, B Dhillon, MS Dennis, et al., Retinal arteriolar geometry is associated with cerebral white matter hyperintensities on magnetic resonance imaging, Int J Stroke, Vol. 5, 2010, pp. 434-9.

86.N Patton, A Pattie, T MacGillivray, T Aslam, B Dhillon, A Gow, et al., The association between retinal vascular network geometry and cognitive ability in an elderly population, Invest Ophthalmol Vis Sci, Vol. 48, 2007, pp. 1995-2000.

87.T Tillin, RM Evans, NW Witt, PS Sharp, PM McKeigue, N Chaturvedi, et al., Ethnic differences in retinal microvascular structure, Diabetologia, Vol. 51, 2008, pp. 1719-22.

88.T Tillin, NG Forouhi, PM McKeigue, and N Chaturvedi, The role of diabetes and components of the metabolic syndrome in stroke and coronary heart disease mortality in u.K. White and african-caribbean populations, Diabetes Care, Vol. 29, 2006, pp. 2127-9.

89.J Birns, R Morris, J Jarosz, H Markus, and L Kalra, Ethnic differences in the cerebrovascular impact of hypertension, Cerebrovasc Dis, Vol. 25, 2008, pp. 408-16.

90.R Crosby-Nwaobi, LZ Heng, and S Sivaprasad, Retinal vascular calibre, geometry and progression of diabetic retinopathy in type 2 diabetes mellitus, Ophthalmologica, Vol. 228, 2012, pp. 84-92.

91.J Ding, CY Cheung, MK Ikram, YF Zheng, CY Cheng, EL Lamoureux, et al., Early retinal arteriolar changes and peripheral neuropathy in diabetes, Diabetes Care, Vol. 35, 2012, pp. 1098-104.

92.MB Sasongko, JJ Wang, KC Donaghue, N Cheung, P Benitez-Aguirre, A Jenkins, et al., Alterations in retinal microvascular geometry in young type 1 diabetes, Diabetes Care, Vol. 33, 2010, pp. 1331-6.

93.RJ Tapp, C Williams, N Witt, N Chaturvedi, R Evans, SA Thom, et al., Impact of size at birth on the microvasculature: the Avon longitudinal study of parents and children, Pediatrics, Vol. 120, 2007, pp. e1225-1228.

94.M Islam, TH Jafar, R Bux, S Hashmi, N Chaturvedi, and AD Hughes, Association of parental blood pressure with retinal microcirculatory abnormalities indicative of endothelial dysfunction in children, J Hypertens, Vol. 32, 2014, pp. 598-605.

95.S Moledina, A de Bruyn, S Schievano, CM Owens, C Young, SG Haworth, et al., Fractal branching quantifies vascular changes and predicts survival in pulmonary hypertension: a proof of principle study, Heart, Vol. 97, 2011, pp. 1245-9.

96.R Kawasaki, MZ Che Azemin, DK Kumar, AG Tan, G Liew, TY Wong, et al., Fractal dimension of the retinal vasculature and risk of stroke: a nested case-control study, Neurology, Vol. 76, 2011, pp. 1766-7.

97.G Liew, P Mitchell, E Rochtchina, TY Wong, W Hsu, ML Lee, et al., Fractal analysis of retinal microvasculature and coronary heart disease mortality, Eur Heart J, Vol. 32, 2011, pp. 422-9.

98.N Cheung, KC Donaghue, G Liew, SL Rogers, JJ Wang, SW Lim, et al., Quantitative assessment of early diabetic retinopathy using fractal analysis, Diabetes Care, Vol. 32, 2009, pp. 106-10.

99.SW Lim, N Cheung, JJ Wang, KC Donaghue, G Liew, FM Islam, et al., Retinal vascular fractal dimension and risk of early diabetic retinopathy: a prospective study of children and adolescents with type 1 diabetes, Diabetes Care, Vol. 32, 2009, pp. 2081-3.

100.J Grauslund, A Green, R Kawasaki, L Hodgson, AK Sjølie, and TY Wong, Retinal vascular fractals and microvascular and macrovascular complications in type 1 diabetes, Ophthalmology, Vol. 117, Jul 2010, pp. 1400-5.

101.R Broe, ML Rasmussen, U Frydkjaer-Olsen, BS Olsen, HB Mortensen, T Peto, et al., Retinal vascular fractals predict long-term microvascular complications in type 1 diabetes mellitus: the danish cohort of pediatric diabetes 1987 (DCPD1987), Diabetologia, Vol. 57, 2014, pp. 2215-21.

102.A Kamiya, J Ando, M Shibata, and H Wakayama, The efficiency of the vascular-tissue system for oxygen transport in the skeletal muscles, Microvasc Res, Vol. 39, 1990, pp. 169-85.

103.MG Schultz, JE Davies, P Roberts-Thomson, JA Black, AD Hughes, and JE Sharman, Exercise central (aortic) blood pressure is predominantly driven by forward traveling waves, not wave reflection, Hypertension, Vol. 62, 2013, pp. 175-82.

104.B Mauroy, M Filoche, ER Weibel, and B Sapoval, An optimal bronchial tree may be dangerous, Nature, Vol. 427, 2004, pp. 633-6.

105.CY Cheung, WT Tay, P Mitchell, JJ Wang, W Hsu, ML Lee, et al., Quantitative and qualitative retinal microvascular characteristics and blood pressure, J Hypertens, Vol. 29, 2011, pp. 1380-91.

106.ED Kurniawan, N Cheung, CY Cheung, WT Tay, SM Saw, and TY Wong, Elevated blood pressure is associated with rarefaction of the retinal vasculature in children, Invest Ophthalmol Vis Sci, Vol. 53, 2012, pp. 470-4.

107.LJ Li, CY Cheung, MK Ikram, P Gluckman, MJ Meaney, YS Chong, et al., Blood pressure and retinal microvascular characteristics during pregnancy: growing up in singapore towards healthy outcomes (GUSTO) study, Hypertension, Vol. 60, 2012, pp. 223-30.

108.G Liew, JJ Wang, N Cheung, YP Zhang, W Hsu, ML Lee, et al., The retinal vasculature as a fractal: methodology, reliability, and relationship to blood pressure, Ophthalmology, Vol. 115, 2008, pp. 1951-6.

109.CC Sng, WL Wong, CY Cheung, J Lee, ES Tai, and TY Wong, Retinal vascular fractal and blood pressure in a multiethnic population, J Hypertens, Vol. 31, 2013, pp. 2036-42.

110.P Zhu, F Huang, F Lin, Q Li, Y Yuan, Z Gao, et al., The relationship of retinal vessel diameters and fractal dimensions with blood pressure and cardiovascular risk factors, PloS One, Vol. 9, 2014, pp. e106551.

111.YT Ong, DA De Silva, CY Cheung, HM Chang, CP Chen, MC Wong, et al., Microvascular structure and network in the retina of patients with ischemic stroke, Stroke, Vol. 44, 2013, pp. 2121-7.

112.M Cavallari, T Falco, M Frontali, S Romano, F Bagnato, and F Orzi, Fractal analysis reveals reduced complexity of retinal vessels in cadasil, PloS One, Vol. 6, 2011, pp. e19150.

113.A Avakian, RE Kalina, EH Sage, AH Rambhia, KE Elliott, EL Chuang, et al., Fractal analysis of region-based vascular change in the normal and non-proliferative diabetic retina, Curr Eye Res, Vol. 24, 2002, pp. 274-80.

114.A Daxer, The fractal geometry of proliferative diabetic retinopathy: implications for the diagnosis and the process of retinal vasculogenesis, Curr Eye Res, Vol. 12, 1993, pp. 1103-9.

115.JW Yau, R Kawasaki, FM Islam, J Shaw, P Zimmet, JJ Wang, et al., Retinal fractal dimension is increased in persons with diabetes but not impaired glucose metabolism: the Australian diabetes, obesity and lifestyle (AusDiab) study, Diabetologia, Vol. 53, 2010, pp. 2042-5.

116.J Grauslund, Eye complications and markers of morbidity and mortality in long-term type 1 diabetes, Acta Ophthalmol, Vol. 89, 2011, pp. 1-19. [Thesis 1].

117.A Karperien, HF Jelinek, JJ Leandro, JV Soares, RM Cesar Jr., and A Luckie, Automated detection of proliferative retinopathy in clinical practice, Clin Ophthalmol, Vol. 2, 2008, pp. 109-22.

118.AC Kunicki, AJ Oliveira, MB Mendonca, CT Barbosa, and RA Nogueira, Can the fractal dimension be applied for the early diagnosis of non-proliferative diabetic retinopathy?, Brazilian J Med Biol Res, Vol. 42, 2009, pp. 930-4.

119.J Lee, BC Zee, and Q Li, Detection of neovascularization based on fractal and texture analysis with interaction effects in diabetic retinopathy, PloS One, Vol. 8, 2013, pp. e75699.

120.S Talu, Multifractal geometry in analysis and processing of digital retinal photographs for early diagnosis of human diabetic macular edema, Curr Eye Res, Vol. 38, 2013, pp. 781-92.

121.CY Cheung, S Ong, MK Ikram, YT Ong, CP Chen, N Venketasubramanian, et al., Retinal vascular fractal dimension is associated with cognitive dysfunction, J Stroke Cerebrovasc Dis, Vol. 23, 2014, pp. 43-50.

122.CY Cheung, YT Ong, MK Ikram, SY Ong, X Li, S Hilal, et al., Microvascular network alterations in the retina of patients with alzheimer’s disease, Alzheimers Dement, Vol. 10, 2014, pp. 135-42.

123.PB Tan, OK Hee, C Cheung, TK Yeo, R Agrawal, J Ng, et al., Retinal vascular parameter variations in patients with human immunodeficiency virus, Invest Ophthalmol Vis Sci, Vol. 54, 2013, pp. 7962-7.

124.B Gopinath, LA Baur, E Teber, G Liew, TY Wong, and P Mitchell, Effect of obesity on retinal vascular structure in pre-adolescent children, Int J Pediatr Obes, Vol. 6, 2011, pp. e353-359.

125.R Wu, CY Cheung, SM Saw, P Mitchell, T Aung, and TY Wong, Retinal vascular geometry and glaucoma: the singapore malay eye study, Ophthalmology, Vol. 120, 2013, pp. 77-83.

126.LS Lim, CY Cheung, C Sabanayagam, SC Lim, ES Tai, L Huang, et al., Structural changes in the retinal microvasculature and renal function, Invest Ophthalmol Vis Sci, Vol. 54, 2013, pp. 2970-6.

127.CC Sng, C Sabanayagam, EL Lamoureux, E Liu, SC Lim, H Hamzah, et al., Fractal analysis of the retinal vasculature and chronic kidney disease, Nephrol Dial Transplant, Vol. 25, 2010, pp. 2252-8.

128.SS Cross, RD Start, PB Silcocks, AD Bull, DW Cotton, and JC Underwood, Quantitation of the renal arterial tree by fractal analysis, J Pathol, Vol. 170, 1993, pp. 479-84.

129.LM Boxt, J Katz, LS Liebovitch, R Jones, PD Esser, and L Reid, Fractal analysis of pulmonary arteries: the fractal dimension is lower in pulmonary hypertension, J Thorac Imaging, Vol. 9, 1994, pp. 8-13.

130.S Haitao, L Ning, G Lijun, G Fei, and L Cheng, Fractal dimension analysis of mdct images for quantifying the morphological changes of the pulmonary artery tree in patients with pulmonary hypertension, Korean J Radiol, Vol. 12, 2011, pp. 289-96.

131.M Helmberger, M Pienn, M Urschler, P Kullnig, R Stollberger, G Kovacs, et al., Quantification of tortuosity and fractal dimension of the lung vessels in pulmonary hypertension patients, PloS One, Vol. 9, 2014, pp. e87515.

Download article (PDF)

Next Article In Issue>

Journal: Artery Research
Volume-Issue: 10 - C
Pages: 1 - 10
Publication Date: 2015/02/24
ISSN (Online): 1876-4401
ISSN (Print): 1872-9312
DOI: 10.1016/j.artres.2015.01.001 How to use a DOI?
Open Access: This is an open access article distributed under the CC BY-NC license.

Cite this article

ris enw bib

TY  - JOUR
AU  - Alun D. Hughes
PY  - 2015
DA  - 2015/02/24
TI  - Optimality, cost minimization and the design of arterial networks
JO  - Artery Research
SP  - 1
EP  - 10
VL  - 10
IS  - C
SN  - 1876-4401
UR  - https://doi.org/10.1016/j.artres.2015.01.001
DO  - 10.1016/j.artres.2015.01.001
ID  - Hughes2015
ER  -

download .riscopy to clipboard